向量基础学习笔记

参考百人计划技术美术，来源bilibli。
1.2.1向量基础
一、什么是向量
1.向量的定义
·向量是有大小和方向的有向线段。
·向量没有位置，只有大小和方向。
·向量的箭头是向量的结束，尾是向量的开始。
·向量描述的位移能被认为是与轴平行的位移序列。
·向量表示：
三维（ax，ay，az） 例（1，4，7） 二维（ax，ay）例（2，-3）

2.向量与标量
·向量：有大小和方向的有向线段。
例：为了打工从秦皇岛坐客车到北京。
·标量：只有大小，没有方向。
例：今天打工加班到十点半，赚了100块。

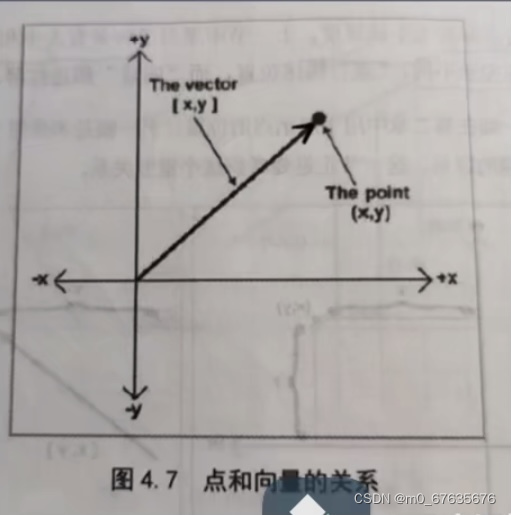
3.向量与点
·向量和点数学形式上相等 但几何意义完全不同。
·点：有位置，没有实际大小或方向。
·向量：无位置，有实际大小和方向。
·联系：
任何一个点都可以看做是从原点出发的向量。


3.零向量
• 零向量是唯一大小为零的向量
•零向量是唯一个设有方向的量
• 零向量不是一个点，因为没有定义某个位置
• 零向量表示的是没有位移，就像零标量表示的是没有数量一样

二、如何计算
1.标量与向量
•加法：x 不可以加减 可乘除
•减法：×
•乘法：将每个分量都与标量相乘就可以
•除法：等同于乘以标量的倒数
例：-2(2,-5)=(-4,10)
例：（6,-