似然函数总结

已于 2023-01-10 22:49:06 修改
阅读量5.1k 收藏 6
点赞数 2
分类专栏： 机器学习 文章标签： 概率论 人工智能
于 2023-01-10 16:38:12 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_65188455/article/details/128632286
版权

在数理统计学中，似然函数（英语：likelihood function）是一种关于统计模型中的参数的函数，表示模型参数中的似然性（英语：likelihood）。似然函数在统计推论中有重大作用，如在最大似然估计和费雪信息之中的应用等等。文字意义上，“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“概率”（或然性）有明确的区分：概率，用于在已知一些参数的情况下，预测接下来在观测上所得到的结果；似然性，则是用于在已知某些观测所得到的结果时，对有关事物之性质的参数进行估值，也就是说已观察到某事件后，对相关母数进行猜测。

一  定义


似然函数是一种关于统计模型中的参数的函数，表示模型参数的似然性。似然函数是给定联合样本值 x 下关于（未知）参数 θ 的函数：

 

二 求似然函数


2.1 离散型随机变量的似然函数


假如离散型随机变量 x 的分布率为P(x|\Theta) ,样本集D上有m个样本，则D上的似然函数为：

 

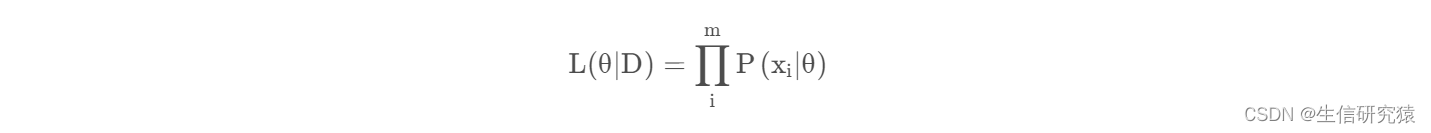
 2.2 连续型随机变量的似然函数


假如连续型随机变量 x 的概率密度函数为 f(x|\Theta) ,样本集D上有m个样本，则D上的似然函数为：

 

 三 具体例子

 

参考链接

https://zh.m.wikipedia.org/zh-hans/%E4%BC%BC%E7%84%B6%E5%87%BD%E6%95%B0

三、 似然函数_cute_Lily的博客-优快云博客_似然函数

(2条消息) 【机器学习】似然函数_sword_csdn的博客-优快云博客_似然函数

似然函数
myc的博客
09-18 3540
似然函数：似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。当给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：L(θ∣x)=P(X=x∣θ)L(\theta|x)=P(X=x|\theta)L(θ∣x)=P(X=x∣θ) 在推断统计学中，“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性...
似然函数 Likelihood Function
06-05
### 似然函数 Likelihood Function #### 一、似然函数的概念 在机器学习与统计学领域中，似然函数（Likelihood Function）是一个至关重要的概念。它主要用于度量一个给定模型参数θ下的数据观测值X的可能性。简单...
机器学习数学基础（2）--最大似然函数
qiaoxinyu1989的博客
07-24 2575
概率是在给定的参数下，某个事件发生的可能性。它是未来事件发生的度量，通常用介于0和1之间的数值表示。
新手村：逻辑回归-理解03：逻辑回归中的最大似然函数
寓教于乐。教己助人
03-25 1282
似然函数Lwb∏i1Nyiyi1−yi1−yiLwbi1∏N​y​iyi​​1−y​i​1−yi​对数似然函数log⁡Lwb∑i1Nyilog⁡yi1−yilog⁡1−yilogLwbi1∑N​yi​logy​i​1−yi​log1−y​i​。
正态MA(0,1)序列的似然函数的一种表示 (2001年)
04-22
总结来说，这篇论文的核心内容是利用数学工具来详细表达正态MA(0,1)序列的似然函数，并通过显式形式将似然函数表示成模型参数的函数。这对统计模型的参数估计和时间序列分析有着重要的理论和实际意义。论文不仅为...
极大似然函数求解_极大似然估计详解
weixin_39804603的博客
12-22 3392
转自:https://blog.youkuaiyun.com/zengxiantao1994/article/details/72787849极大似然估计以前多次接触过极大似然估计，但一直都不太明白到底什么原理，最近在看贝叶斯分类，对极大似然估计有了新的认识，总结如下：贝叶斯决策首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：其中：p(w)：为先验概率，表示每种类别分布的概率；：类条件概率，表示在某种类别前提...
对似然函数的理解
weixin_30955617的博客
09-19 1277
一直对贝叶斯里面的似然函数（likelihood function），先验概率（prior），后验概率（posterior）理解得不是很好，今天仿佛有了新的理解，记录一下。 看论文的时候读到这样一句话： 原来只关注公式，所以一带而过。再重新看这个公式前的描述，细思极恐。 the likelihood function of the parameters θ = {w,α,β} ...
似然函数（Likelihood Function）
...
07-16 3315
假设我们有一组独立同分布（IID）的观察数据X1X2XnX1​X2​Xn​，它们的分布由参数θ\thetaθ决定。似然函数Lθ∣x1x2xnLθ∣x1​x2​xn​定义为当参数为θ\thetaθ时，数据集x1x2xnx1​x2​xn​发生的概率。然而，在似然函数的上下文中，我们考虑参数θ\thetaθ为变量，而观察数据作为固定值。
似然函数是什么
大连赵哥的博客
07-28 1206
似然函数是什么
从最基础来看似然函数
qq_24407657的博客
09-04 636
1.似然函数在百度百科上的定义： 在统计学上，似然函数是一种关于统计模型参数的函数（给定联合样本值x下关于的函数），关于参数的似然函数在数值上等于给定参数后变量X的概率: L(|x)=P(X=x|) 前者是关于的函数，后者是关于x的函数，这里的等号只表示值相等，而不是说两个函数是同一个函数 2.似然函数在统计学上和概率的区别: 概率描述了在给定参数的时候x的的输出结果；似然函数则用来描述...
什么是似然函数？
最新发布
05-07
<think>好的，用户现在想了解似然函数的定义及其在统计学中的作用。之前我们讨论过先验分布，而似然函数在贝叶斯统计中也扮演重要角色，但用户可能更关注其基础概念和频率学派的应用。 首先，我需要明确用户的需求。他们可能刚接触统计学，需要从基本定义入手。我应该先给出似然函数的数学定义，并区分它与概率函数的区别。用户可能混淆这两个概念，所以需要强调参数和观测值的关系。 接下来，用户提到引用中的极大似然估计（MLE）步骤，这可能意味着他们希望了解似然函数如何用于参数估计。需要解释MLE的过程，但要注意引用中的描述是否正确。例如，引用[1]中提到的对数似然函数写法可能有误，应该是乘积的求和，需要确认并纠正。 同时，用户提供的引用[2]涉及朴素贝叶斯分类器，其中使用了似然函数的极大似然估计。这可能意味着用户对似然函数在分类问题中的应用感兴趣，可以结合实例说明，比如在分类中如何估计类条件概率。 用户之前的问题是关于先验分布的，现在转向似然函数，可能需要连接两者，说明在贝叶斯框架中似然函数如何与先验结合形成后验。但用户当前问题更偏向定义，所以重点还是放在似然本身，不过可以简要提及贝叶斯中的应用以保持连贯性。 还要注意用户可能存在的误解，例如认为似然函数是概率分布，但实际上它是参数的函数。需要澄清这一点，并举例说明，比如使用离散和连续的例子来展示似然函数的不同形态。 此外，用户可能想知道似然函数的作用，比如参数估计、模型比较等。需要分点说明，并举例实际应用场景，如逻辑回归中的似然函数使用，或AIC准则中的似然值应用。 最后，检查是否需要回应引用中的内容。引用[1]提到MLE步骤，其中对数似然函数的定义可能有误，应指出正确形式。引用[2]中的似然函数用于朴素贝叶斯，可以结合这个例子进一步解释。 总结回答结构：定义、与概率的区别、MLE过程、作用、贝叶斯中的角色、常见误区。确保语言清晰，避免过多数学公式，但关键公式需用LaTeX标注，符合用户之前的格式要求。最后生成相关问题，帮助用户深入理解。</think>--- ### 似然函数的定义与核心作用解析 --- #### 一、**似然函数的定义** **似然函数**（Likelihood Function）是统计学中用于描述参数$\theta$与观测数据$D$之间关系的核心工具。其数学定义为： $$L(\theta | D) = P(D | \theta)$$ 其中： - $\theta$是待估计的模型参数； - $D$是观测到的数据； - $P(D|\theta)$是给定参数$\theta$时数据$D$的概率（或概率密度）。 **关键区分**： - **概率**：当$\theta$固定时，$P(D|\theta)$表示数据$D$出现的可能性； - **似然**：当数据$D$固定时，$L(\theta | D)$表示不同参数$\theta$对数据生成过程的解释能力[^1]。 **示例**： 假设抛硬币10次出现7次正面，若$\theta$表示正面概率： - **概率视角**：$\theta=0.7$时，$P(D|\theta)=\binom{10}{7}0.7^7(1-0.7)^3$； - **似然视角**：将$D$固定，比较不同$\theta$值的$L(\theta | D)$，如$\theta=0.5$或$\theta=0.8$。 --- #### 二、**似然函数与概率函数的区别** | **维度** | **概率函数** | **似然函数** | |-----------------|----------------------------------|----------------------------------| | **变量** | 数据$D$是变量，$\theta$固定 | 参数$\theta$是变量，数据$D$固定 | | **归一化** | 需满足$\sum_D P(D|\theta) = 1$ | 无需归一化，关注相对大小 | | **核心用途** | 预测数据分布 | 估计参数值 | --- #### 三、**似然函数在统计学中的作用** 1. **参数估计：极大似然估计（MLE）** 通过最大化似然函数求解参数$\theta$的最优值： $$\hat{\theta}_{\text{MLE}} = \arg\max_{\theta} L(\theta | D)$$ **步骤**（以正态分布均值估计为例）： - 定义似然函数：$L(\mu | x_1, \dots, x_n) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_i-\mu)^2}{2\sigma^2}}$； - 取对数简化计算：$\ln L(\mu) = -\frac{n}{2}\ln(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n (x_i - \mu)^2$； - 对$\mu$求导并令导数为零：$\hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i$[^1]。 2. **模型比较与选择** 似然值可用于比较不同模型的拟合优度，例如： - **AIC准则**：$AIC = 2k - 2\ln L$，其中$k$为参数数量，值越小模型越好； - **似然比检验**：比较嵌套模型的似然比统计量$\Lambda = -2\ln\left(\frac{L_{\text{简单}}}{L_{\text{复杂}}}\right)$，服从卡方分布。 3. **贝叶斯推断的桥梁** 在贝叶斯框架中，似然函数与先验分布结合，推导后验分布： $$P(\theta | D) \propto L(\theta | D) \cdot P(\theta)$$ 例如，在朴素贝叶斯分类器中，类条件概率$P(x^{(i)}|c)$通过极大似然估计确定[^2]。 --- #### 四、**案例分析：逻辑回归中的似然函数** 在二分类逻辑回归中，假设输出变量$y \in \{0,1\}$，模型概率为： $$P(y=1 | x, \beta) = \frac{1}{1 + e^{-\beta^T x}}$$ 似然函数定义为所有样本预测概率的乘积： $$L(\beta) = \prod_{i=1}^n P(y_i | x_i, \beta)^{y_i} \cdot (1 - P(y_i | x_i, \beta))^{1-y_i}$$ 对数似然函数为： $$\ln L(\beta) = \sum_{i=1}^n \left[ y_i \ln P(y_i | x_i, \beta) + (1-y_i) \ln (1 - P(y_i | x_i, \beta)) \right]$$ 通过梯度上升法最大化$\ln L(\beta)$，得到参数估计$\hat{\beta}$。 --- #### 五、**常见误区与注意事项** 1. **似然函数不是概率分布** 似然函数对参数$\theta$无归一化性质，仅反映相对可能性。 2. **数据量敏感性** 小样本下MLE可能过拟合，需结合正则化（如MAP估计引入先验）。 3. **数值稳定性问题** 实际计算中常使用对数似然避免浮点数下溢。 --- ### 相关问题 1. 如何解释极大似然估计的渐近正态性？ 2. 似然函数在贝叶斯估计和频率学派估计中的角色有何异同？ 3. 为什么逻辑回归使用对数似然而非普通似然进行优化？ --- **注**：似然函数是连接数据与模型参数的纽带，其最大化过程本质是寻找最能解释观测数据的参数值[^1][^2]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值