一次性搞懂排序算法，常用的排序算法总结，mongodb教程导入外部数据

---

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾，以此类推，直到所有元素均排序完毕

由于存在数据交换，选择排序不是稳定的排序算法

实现

public class SelectionSort {

public int[] selectionSort(int[] A, int n) {

//记录最小下标值

int min=0;

for(int i=0; i<A.length-1;i++){

min = i;

//找到下标i开始后面的最小值

for(int j=i+1;j<A.length;j++){

if(A[min]>A[j]){

min = j;

}

}

if(i!=min){

swap(A,i,min);

}

}

return A;

}

private void swap(int[] A,int i,int j){

int temp = A[i];

A[i] = A[j];

A[j] = temp;

}

}

插入排序

---

插入排序算法的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入，因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间

实现

public class InsertionSort {

public int[] insertionSort(int[] A, int n) {

//用模拟插入扑克牌的思想

//插入的扑克牌

int i,j,temp;

//已经插入一张，继续插入

for(i=1;i<n;i++){

temp = A[i];

//把i前面所有大于要插入的牌的牌往后移一位，空出一位给新的牌

for(j=i;j>0&&A[j-1]>temp;j–){

A[j] = A[j-1];

}

//把空出来的一位填满插入的牌

A[j] = temp;

}

return A;

}

}

归并排序

---

归并排序核心是分治思想，先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了

若将两个有序表合并成一个有序表，称为二路归并

归并排序是稳定的排序算法

实现

public class MergeSort {

public static void main(String[] args) {

int data[] = { 9, 5, 6, 8, 0, 3, 7, 1 };

megerSort(data, 0, data.length - 1);

System.out.println(Arrays.toString(data));

}

public static void mergeSort(int data[], int left, int right) { // 数组的两端

if (left < right) { // 相等了就表示只有一个数了 不用再拆了

int mid = (left + right) / 2;

mergeSort(data, left, mid);

mergeSort(data, mid + 1, right);

// 分完了 接下来就要进行合并，也就是我们递归里面归的过程

merge(data, left, mid, right);

}

}

public static void merge(int data[], int left, int mid, int right) {

int temp[] = new int[data.length]; //借助一个临时数组用来保存合并的数据

int point1 = left; //表示的是左边的第一个数的位置

int point2 = mid + 1; //表示的是右边的第一个数的位置

int loc = left; //表示的是我们当前已经到了哪个位置了

while(point1 <= mid && point2 <= right){

if(data[point1] < data[point2]){

temp[loc] = data[point1];

point1 ++ ;

loc ++ ;

}else{

temp[loc] = data[point2];

point2 ++;

loc ++ ;

}

}

while(point1 <= mid){

temp[loc ++] = data[point1 ++];

}

while(point2 <= right){

temp[loc ++] = data[point2 ++];

}

for(int i = left ; i <= right ; i++){

data[i] = temp[i];

}

}

}

希尔排序

---

基本思想：

算法先将要排序的一组数按某个增量d（n/2，n为要排序数的个数）分成若干组，每组中记录的下标相差d，对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成

希尔排序法(缩小增量法) 属于插入类排序，是将整个无序列分割成若干小的子序列分别进行插入排序的方法

假如：数组的长度为10，数组元素为：25、19、6、58、34、10、7、98、160、0

整个希尔排序的算法过程如下如所示：

实现

public static int[] ShellSort(int[] array) {

int len = array.length;

int temp, gap = len / 2;

while (gap > 0) {

for (int i = gap; i < len; i++) {

temp = array[i];

int preIndex = i - gap;

while (preIndex >= 0 && array[preIndex] > temp) {

array[preIndex + gap] = array[preIndex];

preIndex -= gap;

}

array[preIndex + gap] = temp;

}

gap /= 2;

}

return array;

}

快速排序

---

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

• 先从数列中取出一个数作为基准数。

• 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

• 再对左右区间重复第二步，直到各区间只有一个数。

实现1

public class QuickSort {

public static void quickSort(int[]arr,int low,int high){

if (low < high) {

int middle = getMiddle(arr, low, high);

quickSort(arr, low, middle - 1);//递归左边

quickSort(arr, middle + 1, high);//递归右边

}

}

public static int getMiddle(int[] list, int low, int high) {

int tmp = list[low];

while (low < high) {

while (low < high && list[high] >= tmp) {//大于关键字的在右边

high–;

}

list[low] = list[high];//小于关键字则交换至左边

while (low < high && list[low] <= tmp) {//小于关键字的在左边

low++;

}

list[high] = list[low];//大于关键字则交换至左边

}

list[low] = tmp;

return low;

}

}

实现2

public class QuickSort {

public static void quickSort(int data[], int left, int right) {

int base = data[left]; // 基准数，取序列的第一个

int ll = left; // 表示的是从左边找的位置

int rr = right; // 表示从右边开始找的位置

while (ll < rr) {

// 从后面往前找比基准数小的数

while (ll < rr && data[rr] >= base) {

rr–;

}

if (ll < rr) { // 表示是找到有比之大的

int temp = data[rr];

data[rr] = data[ll];

data[ll] = temp;

ll++;

}

while (ll < rr && data[ll] <= base) {

ll++;

}

if (ll < rr) {

int temp = data[rr];

data[rr] = data[ll];

data[ll] = temp;

rr–;

}

}

// 肯定是递归 分成了三部分,左右继续快排，注意要加条件不然递归就栈溢出了

if (left < ll)

quickSort(data, left, ll - 1);

if (ll < right)

quickSort(data, ll + 1, right);

}

}

优化

基本的快速排序选取第一个或最后一个元素作为基准。但是，这是一直很不好的处理方法

如果数组已经有序时，此时的分割就是一个非常不好的分割。因为每次划分只能使待排序序列减一，此时为最坏情况，快速排序沦为冒泡排序，时间复杂度为O(n^2)

三数取中

一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元

举例：待排序序列为：8 1 4 9 6 3 5 2 7 0

左边为：8，右边为0，中间为6

我们这里取三个数排序后，中间那个数作为枢轴，则枢轴为6

插入排序

当待排序序列的长度分割到一定大小后，使用插入排序 原因：对于很小和部分有序的数组，快排不如插排好。当待排序序列的长度分割到一定大小后，继续分割的效率比插入排序要差，此时可以使用插排而不是快排

重复数组

在一次分割结束后，可以把与Key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割

在一次划分后，把与key相等的元素聚在一起，能减少迭代次数，效率会提高不少

具体过程：在处理过程中，会有两个步骤

第一步，在划分过程中，把与key相等元素放入数组的两端

第二步，划分结束后，把与key相等的元素移到枢轴周围

举例：

待排序序列 1 4 6 7 6 6 7 6 8 6

三数取中选取枢轴：下标为4的数6

转换后，待分割序列：6 4 6 7 1 6 7 6 8 6

枢轴key：6

第一步，在划分过程中，把与key相等元素放入数组的两端

结果为：6 4 1 6(枢轴) 7 8 7 6 6 6

此时，与6相等的元素全放入在两端了

第二步，划分结束后，把与key相等的元素移到枢轴周围

结果为：1 4 6 6(枢轴) 6 6 6 7 8 7

此时，与6相等的元素全移到枢轴周围了

之后，在1 4 和 7 8 7两个子序列进行快排

堆排序

---

堆是一种特殊的树。只要满足这两点，它就是一个堆。

• 堆是一个完全二叉树；

• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。

对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

一般升序用大根堆，降序就用小根堆

如何实现一个堆

完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。

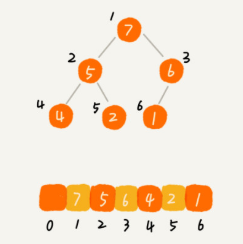
比如查找数组arr中某个数的父结点和左右孩子结点，比如已知索引为i的数，那么

1. 父结点索引：(i-1)/2（这里计算机中的除以2，省略掉小数）

2. 左孩子索引：2*i+1

3. 右孩子索引：2*i+2

所以堆的定义性质：

• 大根堆：arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2)

• 小根堆：arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)

《一线大厂Java面试题解析+后端开发学习笔记+最新架构讲解视频+实战项目源码讲义》

【docs.qq.com/doc/DSmxTbFJ1cmN1R2dB】 完整内容开源分享

堆排序基本步骤

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

以下将针对数组arr[1,2,5,4,3,7]进行大顶堆的数据结构转换。

• 我们从最后一个非叶子结点开始（第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是索引为2的结点），从右至左，从下至上进行调整

• 由于[5,7]中7元素最大，5和7交换。

• 最后一个非叶子结点索引减1，找到第二个非叶结点(索引1)，由于[4,3,2]中4元素最大，2和4交换。

• 非叶子结点索引减1，找到第三个非叶结点(索引0)，由于[4,1,7]中7元素最大，1和7交换。

• 这时，交换导致了子根[1，5]结构混乱，继续调整，[1,5]中5最大，交换1和5。

• 此时，我们就将一个无序序列构造成了一个大顶堆。

• 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换

• 最后，就实现了堆排序

实现

import java.util.Arrays;

public class HeapSort {

public static void main(String[] args) {

int data[] = { 8, 4, 20, 7, 3, 1, 25, 14, 17 };

heapSort(data);

System.out.println(Arrays.toString(data));

}

public static void maxHeap(int data[], int start, int end) {

int parent = start;

int son = parent * 2 + 1; // 下标是从0开始的就要加1，从1就不用

while (son < end) {

int temp = son;

// 比较左右节点和父节点的大小

if (son + 1 < end && data[son] < data[son + 1]) { // 表示右节点比左节点大

temp = son + 1; // 就要换右节点跟父节点

}

// temp表示的是 我们左右节点大的那一个

if (data[parent] > data[temp])

return; // 不用交换

else { // 交换

int t = data[parent];