Summary Ⅰ

第一单元设计测试思路

第一部分--类的定义与设计

第一节：功能结构分析

题目最本质的要求是“合理展开表达式“，而展开意味着计算。（紧扣题意）

第一种最简单展开：+(...)+ -->直接去括号即可；

第二种：简单乘法展开：m*(...) -->对括号内结构进行顺次遍历和变化；

第三种：复杂乘法展开：(...)*(...) -->双遍历和变化；

其中对于幂展开：(...)**m -->m次遍历和变化 ；

通过以上分析，可以发现如果括号内数据的结构不定，功能的结构也无法设计，因此顺理成章地进行结构分析

第二节：数据结构分析

• ：表达式由项组成，项之间通过加减运算符连接
• ：项由因子组成，因子之间通过乘运算符连接
• ：因子有多种 ：

常数因子，带符号整数，不带指数 ；

变量因子：带指数，；

三角函数因子：带指数；

函数因子：不带指数；

求导因子：不带指数；

表达式因子：复合结构 (表达式)主要需要考虑三种组织结构：顺序结构 • 层次结构 • 嵌套结构，并且带因子

（因子种类庞大，不符合结构精简的原则，下面会观察因子与因子之间的联系进行优化）

• ：项Term中可以包含任意因子；（Term也可以继承Factor成为一种因子）

基于对数据结构的分析，可以得出数据之间的层次关系

第三节：类的识别与设计

表达式类(Expr) ： 管理顺次相连的项对象 ， 管理作用于相邻项对象的加或减操作符

项类(Item) ：管理顺次相连的因子对象

因子类(Factor) ：由于因子种类较多，因此选择性进行合并：将常数因子和变量因子整合为Normal类因子，三角函数为Trig因子，求导因子为Der因子，函数因子为Func因子，表达式为Expr因子

    

前三节均为掌握题旨之后进行的初步思考和审视，是对代码结构框架的宏观设计，下面将进入到题目的内核

第四节：展开计算

简单乘法展开：针对表达式中的每个项乘以一个因子

复杂乘法展开 ：两个表达式中的项两两相乘

幂展开 ：多次应用乘法展开

展开之后的表达式中每一项 ，表示形式可统一：系数*X**幂*Y**幂*Z**幂*三角函数*三角函数

注意：如上展开可以表示为：Norm*Trig*Trig… 即：每个最简项只有一个Norm和多个Trig，但是，并不含有Func，Der，Expr等复杂因子，这三种因子展开后都可以被化简为如上形式

先从宏观考虑最后的结果，再思考如何到达结果

第五节：类的三种主要角色

• 关注于输入输出处理的类

输入扫描 • 基于层次化正则 • 基于递归下降 • 结果：得到一系列因子（字符串）和连接操作符(字符串)

格式化输出 • 连接操作符的表示不必冗余存储 • 必要的输出格式

•  关注于对象管理的类

对象管理类提供统一的对象构造方法：以切分后的字符串（或者解析后的数值）为输入，自动调用相关的类来构造对象 parseExpr, parseTerm, parseFactor

通过Expression类来管理项对象，形成项对象容器

通过Item类来管理这些因子对象，形成因子对象容器

考虑几个问题：

何时创建ExprFactor对象？

创建时对输入字符串的扫描处理与输入输出类的扫描处理是否有区别？

哪个类需要提供展开功能？（最关键）

哪些类需要提供合并功能？（设计优化）

第二部分--优化（基于功能实现）

狭义优化：

传统优化方法有两种：一种为拿到最终结果后进行合并优化；另一种为在处理过程中进行相关优化。

我选择了第二种，不仅因为该方法体现了分治的思想，还因为该方法可以带来其他效益，见下。下面进行简述：

从最底层的Norm，Trig主要根据自身类的特性进行化简（如指数为0的处理等），将优化结果呈递到Term，Term处进行Factor的同类项合并，显然上述四种Factor分类之间不存在不同Factor之间可以合并的情况，即只有同类Factor才可以进行合并。此处优化方式为：保证Term内元素的有序性，自定义Factor等级，Norm > Trig > Func > Expr > Der

Term内项的有序性可以有效缓解项合并的复杂性，准确来说，既方便了同类项的查找匹配以及插入或者合并，又方便了顶层Expr的合并。

这里仅简述狭义优化，具体的实现过程见下文实现阶段。

广义优化：

广义“优化”不仅包含最后对于结果的处理，还包含实现过程中对于思维的优化，后者与递归下降的本质息息相关。所以先来谈谈对于递归下降的见解。

** 递归下降

显然，递归下降的本质为递归函数，不过并非传统意义上的单递归函数，如（斐波那契数列，爬楼梯），而是综合型递归，也就是在朴素递归中引入了更多的分支，易感乱花渐欲迷人眼。但是，如果我们在每次进行分支时，就像老师说的，只想当前一步，就不会错乱。

下面我们来看下这个庞大的递归函数的结构：

哪个是递归函数呢？顶层的parseExpr函数；

递归参数？字符串；

函数返回值？Expr变量；

递归出口？ parseFactor -> parseTerm ->parseExpr

递归内部实现？parseExpr -> parseTerm ->parseFactor

递归体现在哪里？一般来说，递归函数会调用自己进行递归，那么这个递归函数的递归特性体现在哪里呢？parseFactor中 判断出parentheses后调用parseExpr，实现自我调用，凸显递归本质。

那么，递归是如何紧紧依赖优化的？前面说的追踪递归容易跟丢，又是怎么回事？

随着这个问题的抛出，我们也来到了本单元作业的核心：字符串展开问题。

首先回答上面的问题，“哪个类需要提供展开功能？”，固然是三个因子：Func，Der；Func，Der这两个因子都不是最简形式，化简完之后的结果必然是Expr；同时，由于我们只是做了初步展开，所以化简之后的Expr并不是最简形式，因此，Expr类要有合并功能。

至此，我们完成了对于题目的局部分析，接下来需要进行实际的操作来串联各个组件，以验证上述思路的可行性。

摆在我们面前的问题是：什么时候进行展开，什么时候合并，在哪里进行优化？

顺藤摸瓜，从递归函数parseExpr开始推理。

parseExpr(+,-) -> parseTerm(*) ->

parseFactor { parseExpr, parseFunc, parseNorm, parseTrig, parseDer } ->

parseTerm (*) -> parseExpr(+,-)

第三步得到parseFactor之后，该Factor被pull入Term中，pull的过程需要进行同类项合并，此处，对Term中的factors进行sort 以及merge，便于快速合并同类项，不同的Factor，有不同的merge方法，注意，在此处不需要展开Expr，Func，Der因子，一个简单的设计原则是，非必要。接下来，Term被呈递到Expr处（+,-），可以看到此时来到了处理流程的最后一步，Expr的合并。因此，Func，Der，Expr要在此时进行展开，并且展开到最简形式。但是，我们在Expr处的视野里只有Term，所以，这个展开函数应该是针对Term的。这也告诉我们，展开的位置和展开的对象不是必然相同的。Term中，我们需要展开每个Factor，并将这些复杂的Factor都转化为Expr，此处的原因是归一化处理，由于Expr，Func等因子展开后的形式极有可能是Expr形式，因此对于Term中的每个Factor，我们都选择展开为Expr，并且在Term方法中实现展开后的合并优化。

第三部分-- Bug集中分析：

（三次作业中发现的Bug主要集中在第二三次作业。）

• 第二次作业有两个Bug：

第一个属于失误Bug，原因是自己并没有删去用于本地测试时的提示信息输出，导致输出冗杂；第二个Bug出在优化问题上，对三角函数内部表达式的优化稍欠考虑，错认为其内部表达式的第一个项为三角因子则整个表达式即为三角因子，优化的目的是为了去掉三角函数可能存在的冗余括号，却不慎缺少了必要的括号；

• 第三次作业主要的Bug有三处，三个bug都相当隐蔽：

第一个bug是：在三角因子优化的时候，由于其内部被设计为了表达式，因此递归调用parseExpr可以得到理论上的最简形式，但是，由于优化处理，导致优化后的Expr.toString并不能得到最简形式，比如1+cos(0),经过处理后得到1+1，却忽略了1+1还可以继续进行合并，这属于处理上的不当。因为自己写的toString也是不断调用Term和Factor的toString得到字符串并进行拼接，并没有再深一步考虑得到的这些因子之间在化简之后可能的合并关系，本质上属于架构问题，优化之后的项并没有进行彻底有效的合并，甚至将一部分优化放在了字符串转换上，这样得到的结果是只是形式上的优化，并不是实体优化。因此最终得到的字符串并不是最简字符串，中间递归调用parseExpr得到的字符串也不是最简的，很可能导致优化出问题。   

第二个问题是TimSort问题：将优化分散到每个Factor和每个Term，为了方便合并同类项选择了先排序再合并，但由于自己的排序函数并没有出现达到自反性，对称性，导致排序函数出问题；具体报错信息如下：

Comparison method violates its general contract!

（没有满足可逆比较）

测试点：

2

f(x)=x*sin(x)

g(x)=(2+x-sin(x))**3

0-((y+1)*cos(0)**2-f(0))*g(z)

Solution：System.setProperty("java.util.Arrays.useLegacyMergeSort", "true");

TLE测试点：

3

f(x)=cos(x)

g(x,y)=cos((-y))*cos(x)-sin((-y))*sin(x)

h(y,x)=f(x)*sin(y)*f(x)+sin(y)*sin(y)*sin(x)

dx((-(x*x-5))- ((g(sin(x),f(sin(x)**1)))**+2))+h((x*g(x**2,(x*x))),x)

solution：经过测试发现，求导耗费时间较长，优化方式为：若当前因子中不包含待求导因子，则直接返回0，无需按照表达式的要求进行逐步递归求导，可以大大提高效率。经修改，节约了8s左右，成功AC

第四部分--研讨课交流收获

第二次作业选择了重构，研讨课上组员特别强调了对于函数替换的情况，为了防止形如f(x) = x**2 ; f(x**2) = x**2**2的情况出现，选择给每个形式参数都带上括号，即展开后结果为：(x**2)**2。令人受益匪浅，同时，有同学提出，如何对sin**2 + cos**2的合并，以及sin(x)cos(y) + cos(x)sin(y) = sin((x+y))的合并，也让人耳目一新。

第五部分--程序质量分析

第一节：基于度量来分析程序结构

• 使用的类有：Cal，Der，Expr，Factor，Func，Lexer，Main，Norm，Parse，ProcessStr，Term，Trig
  • 

        Cal：保存函数计算方法的计算类；

        字段：保存函数的操作运算符和形参的传递顺序

        无方法；

        Factor：接口：

           定义方法有：compareToFactor，canMergeWithFactor，mergeWithFactor，canInsertBefore，myclone

     所以所有继承自Factor的因子类都重写了如上方法，故不在赘述

        Der：求导因子类；

        字段：求导的对象和带求导表达式

        方法：转化为Expr（展开时，Der因子会被展开为Expr形式）

         Expr：表达式因子：

        字段：ArrayList<Term> 以及 exponent

           方法：用于排序与合并类的比较方法；Expr*Expr，Expr+(-)Expr；derive求导方法；toString方法；

          

        Func：函数因子

           字段：ArrayList<Expr> (用于保存运算的实参)；Cal，计算的类，即该函数的计算方式

           方法：parseToExpr，展开后为Expr

        Norm：常规因子

           形式：系数*x**指数*y**指数*z**指数

               故字段有Arraylist<BigInteger>表示一个系数和三个指数

        方法：addNorm，mulNorm，derive(求导)，fixExp(优化指数为0或者为1)

        Trig：三角函数因子

        字段：sinCos，expr（内嵌表达式），exponent（指数）

        方法：derive；fixExponent（优化指数）

        Term：项

               字段：ArrayList<Factor>

        方法：pullFactor（加入新的Factor），mulTerm，sameToTerm，compareToTerm（用于排序和比较），sort

        Lexer和Parser类为词法和语法分析器，较为常规

ProcessStr为常用的字符串处理函数，其中函数为静态方法

第二节：计算经典的OO度量，分析类的内聚和相互间的耦合情况

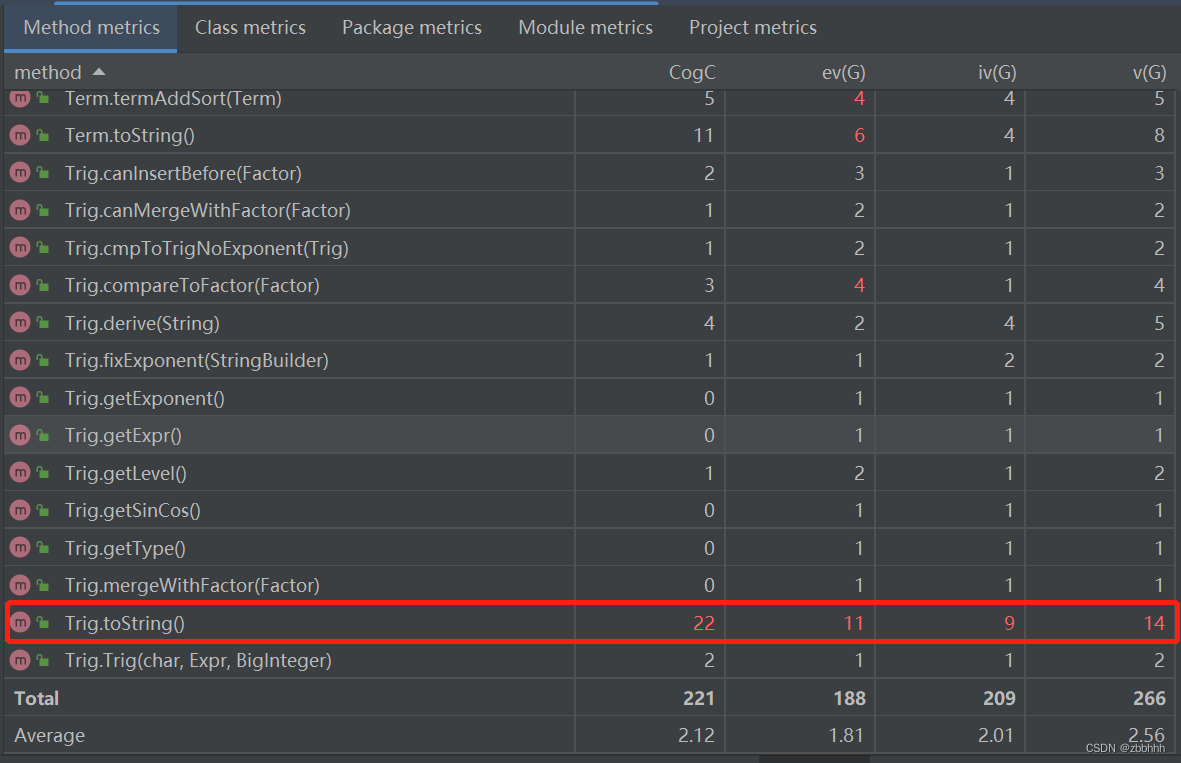分析：Trig和parseFactor与其他模块的耦合度较高。

parseFactor与其他模块的耦合度较高原因是：parseFactor作为分支函数，会进行复杂度较高的分流工作，将抽象的parseFactor转化为具体的parseFunc，parseExpr，parseDer等，因此作为中转分支枢纽，自然耦合度较高；

Trig与其他模块的耦合度较高原因是：Trig中含有Expr因子，Expr因子中可以包含多个Term和Factor，这在一定程度上增加了耦合度；同时Trig求导尤其复杂，在求导过程中，涉及对内嵌因子的递归求导，不仅加大了求导难度和而且大大增加了与各种内嵌因子的耦合程度。可以形象地说，三角因子不过是Expr因子套上sin/cos外套而已。

第三节：架构设计体验

Ⅰ.分析自己程序的bug

• 对比分析出现了bug的方法和未出现bug的方法在代码行和圈复杂度上的差异
• 两次出现bug的位置都是Trig优化处。Trig类本身与其他模块的耦合程度较高，很容易成为bug暴露处。另外，Trig的优化函数是最具有灵活性的函数，考虑到三角函数的可变性很强，比如sin^2+cos^2 = 1，sin(0)=0,cos(0)=1,二倍角公式，立方合并等等，优化函数是一个易触雷的位置。复杂度也明显高于其他子类的优化函数。最好的优化方式是：树形分类，先在草稿纸上按照自己所能想到的几个可能的大类进行初步较粗糙的分类，然后进入分支，考虑细节的优化可能性。但是，这样仍然难以做到全面，最后还需要经过有效数据进行求证，进一步晚上自己的优化树，有了优化树作为基础分支支撑，测试得到的其他特异优化再想加入优化树并不难。

 

Ⅱ.分析自己发现别人程序bug所采用的策略

• 设计测试数据上，并不是使用评测机大规模大规模计算，更多地考虑的是偏难怪数据。切口点一般为多级括号嵌套，尽量在在嵌套过程中实现三角函数，自定义函数的复杂性。

第六部分--心得体会

方法论：面对困难千万不能放弃，在没有思路的情况下，最好的前进方式是耐心品味老师的指导（比如ppt），老师的设计思路一定值得我们去品鉴，很多时候是我们唯一合理的突破点。

感受：对于也许你也会在梦中惊醒，但请尽量保持镇定和勇敢，前方的每一个困难都有其存在的必要与意义，逃避无济于事，更是不正确的。想一览众山小，需先有凌云之志，难凉热血！