机器学习——Logistic回归_sigmoid函数缩放特征映射-优快云博客

本文链接：https://blog.youkuaiyun.com/m0_63038557/article/details/134782651

1. 介绍

1.1简介

在机器学习领域，Logistic回归是一种经典的二分类算法，常用于解决问题，例如垃圾邮件分类、疾病诊断等。与线性回归不同，Logistic回归使用S形函数将线性输出映射到概率空间，使其可以处理分类问题。

1.2. Logistic回归概述

Logistic回归是一种统计学习方法，用于建模二分类问题。它通过一个线性方程的组合，将输入特征映射到S形函数（sigmoid函数）上，得到一个0到1之间的概率值。这个概率值可以用于判断样本属于类别1的可能性。

2.数学基础

2.1 模型表达式

Logistic回归的模型表达式如下：

$P(Y=1|X)=\frac{1}{1+e^{-(\beta _{0}+\beta _{1}X_{1}+...+\beta _{n}X_{n})}}$

这里：

P(Y=1∣X) 是给定输入 X 条件下输出为1的概率。
e 是自然对数的底。
β0,β1,…,βn 是模型参数。
X1,…,Xn 是输入特征。

这个方程的核心是线性组合 $\beta _{0}+\beta _{1}X_{1}+...+\beta _{n}X_{n}$ ，该线性组合表示输入特征与相应参数的加权和。Sigmoid函数将这个线性组合的结果映射到0到1之间的概率值。

2.2 最小二乘法

最小二乘法的线性回归模型表达式为：

$Y=\beta _{0}+\beta _{1}X_{1}+...+\beta _{n}X_{n}+\varepsilon$

其中：

Y 是目标变量（要预测的数值）。
X1,…,Xn 是输入特征。
β0,…,βn 是模型参数。
ϵ 是误差项，表示模型不能解释的部分。

最小二乘法目标

最小二乘法的目标是最小化残差平方和，即最小化观测值与模型预测值之间的差异：

$Minimize\sum _{i=1}^{N}(Y_{i}-(\beta _{0}+\beta _{1}X_{i1}+...+\beta _{n}X_{in}))^{2}$

这里 N 是样本数量。

2.3 Sigmoid函数

Logistic回归中使用的Sigmoid函数是一个S形函数，其表达式为：

$S(x)=\frac{1}{1+e^{-x}}$ , 图像如下：

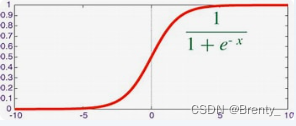
Sigmoid函数将任意实数X映射到0到1之间。在Logistic回归中，Sigmoid函数的输入是线性组合 β0+β1X1+…+βnXn，输出是0到1之间的概率值。这个非线性变换是Logistic回归的关键，使其能够处理二分类问题。

3. 模型训练过程

Logistic回归的训练过程涉及到梯度下降算法、损失函数和最大似然估计。

梯度下降算法： 通过梯度下降，模型参数 β 被调整以最小化损失函数。梯度下降的目标是找到使得损失函数达到最小值的参数值。
损失函数： 在Logistic回归中，常用的损失函数是对数似然损失函数。最小化这个损失函数等价于最大化观测到数据的似然。
最大似然估计： 通过最大似然估计，模型的参数被调整以使观测到的数据的似然最大化。最大似然估计是统计学中常用的一种参数估计方法。

4.代码实例

这段代码将演示如何使用Logistic回归模型对鸢尾花数据集进行分类，并通过可视化模型的决策边界及其在测试集上的性能。

4.1导入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
from sklearn.datasets import load_iris

numpy：用于数学运算。
pandas：用于数据处理和创建数据框。
matplotlib.pyplot：用于绘图。
seaborn：用于绘制数据分布和决策边界。
sklearn：包含了用于机器学习的多个工具，如模型选择、预处理、评估等。
load_iris：用于加载鸢尾花数据集。

4.2载入数据集并进行划分

# 载入鸢尾花数据集
iris = load_iris()
X = iris.data[:, :2]  # Use only the first two features
y = iris.target

# 创建数据框
columns = ['sepal_length', 'sepal_width']
df = pd.DataFrame(data=X, columns=columns)
df['target'] = y

# 打印鸢尾花数据集的前几行
print("Iris Dataset:")
print(df.head())

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 特征缩放（标准化）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 打印训练集和测试集
print("\nTraining Set:")
print(pd.DataFrame(data=X_train_scaled, columns=columns).head())
print("\nTesting Set:")
print(pd.DataFrame(data=X_test_scaled, columns=columns).head())

4.2.1载入鸢尾花数据集：
使用load_iris函数加载鸢尾花数据集。
4.2.2划分训练集和测试集：
使用train_test_split函数将数据集划分为训练集和测试集。
4.2.3特征缩放（标准化）：
使用StandardScaler对特征进行标准化，以便它们具有相似的尺度。

4.3运用Logistic回归模型

# 创建Logistic回归模型
model = LogisticRegression(random_state=42)

# 训练模型
model.fit(X_train_scaled, y_train)

# 预测
y_pred = model.predict(X_test_scaled)

# 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
print(f'\nAccuracy: {accuracy:.2f}')

# 打印分类报告
print('\nClassification Report:')
print(classification_report(y_test, y_pred))

4.3.1创建Logistic回归模型：使用LogisticRegression创建Logistic回归模型。
训练模型：使用训练集训练Logistic回归模型。
4.3.2预测：使用测试集进行模型预测。
4.3.3评估模型性能：计算并打印模型的准确度。打印分类报告，包括精确度、召回率、F1值等。

4.4可视化

# 使用Seaborn绘制决策边界和数据点的分布
plt.figure(figsize=(10, 6))

# 绘制训练集数据点
sns.scatterplot(x='sepal_length', y='sepal_width', hue='target', data=df, palette='viridis', marker='o', s=100)

# 绘制测试集数据点
sns.scatterplot(x=X_test_scaled[:, 0], y=X_test_scaled[:, 1], hue=y_pred, palette='viridis', marker='X', s=200, edgecolor='black', linewidth=1)

# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创建网格以评估模型
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 100), np.linspace(ylim[0], ylim[1], 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])

# 将预测结果放入颜色图中
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap='viridis', alpha=0.3)

plt.title('Logistic Regression Decision Boundary')
plt.xlabel('Sepal Length (scaled)')
plt.ylabel('Sepal Width (scaled)')

plt.legend(['Setosa', 'Versicolor', 'Virginica', 'Predicted Setosa', 'Predicted Versicolor', 'Predicted Virginica'])
plt.show()

5.常见问题和挑战

多重共线性： 当特征之间存在高度相关性时，Logistic回归模型可能变得不稳定，导致系数估计不准确。这种情况下，可能需要采取措施，如特征选择或使用正则化方法（如LASSO或岭回归）。
样本不平衡： 如果类别分布不均匀，即正类别和负类别的样本数量相差悬殊，模型可能偏向于出现频率较高的类别。在这种情况下，需要使用一些技术手段来平衡类别，如过采样、欠采样或使用不同的评估指标。
特征缺失： 如果样本中存在缺失的特征，Logistic回归模型可能无法处理。需要进行数据清理或采取适当的缺失值处理策略。
非线性关系： Logistic回归是一个线性模型，对于非线性关系的建模效果可能较差。在面对非线性问题时，可以考虑使用更复杂的模型，或者对特征进行转换以引入非线性关系。
噪声和异常值： 噪声和异常值可能对模型的性能产生负面影响。需要进行异常值检测和处理，以确保模型对噪声的影响降到最低。
过拟合： 如果模型过于复杂，可能在训练集上表现良好，但在未见过的数据上表现较差。需要采取措施，如正则化，以防止过拟合。

6.总结

Logistic回归的一般步骤：

1. 数据收集：收集包含特征和标签的数据集。特征是影响预测的变量，标签是我们想要预测的目标变量。

2. 数据预处理：对数据进行预处理，包括处理缺失值、处理异常值、特征缩放等。确保数据的质量对模型训练至关重要。

3. 特征工程：进行特征工程，选择合适的特征，处理高维度数据，解决多重共线性等问题。特征工程的质量直接影响模型性能。

4. 数据划分：将数据集划分为训练集和测试集。训练集用于训练模型，测试集用于评估模型的性能。

5. 模型构建：使用Logistic回归算法构建模型。Logistic回归是一个线性模型，通过逻辑函数将线性组合映射到概率空间。

6. 模型训练：使用训练集对模型进行训练。训练的过程是通过最大化似然估计或最小化损失函数来调整模型参数。

7. 模型评估：使用测试集评估模型的性能。常用的评估指标包括准确率、精确度、召回率、F1分数等。

8. 参数调优：根据模型的性能进行参数调优。可以尝试不同的正则化参数、学习率等来优化模型。

9. 模型应用：当模型经过训练和调优后，在新的未见数据上进行预测。可以将模型部署到实际应用中。

心得：

Logistic回归是解决二分类问题的一种强大工具，广泛应用于实际场景，如信用评分、垃圾邮件检测等。通过解决鸢尾花分类问题，将Logistic回归应用到实际案例中，加深对算法在实际场景中应用的理解。特征工程对模型性能有显著影响。对数据进行预处理和特征工程，可以提高模型的准确性和泛化能力。通过可视化决策边界和数据分布，更直观地理解模型的学习过程和预测效果。总体而言，Logistic回归是一个简单而有效的分类算法，适用于许多实际问题。其简洁的数学表达和较好的解释性使其成为机器学习入门的重要工具。