机器学习之决策树

最新推荐文章于 2025-11-13 12:49:04 发布

原创最新推荐文章于 2025-11-13 12:49:04 发布 · 1.8k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#python

Python 专栏收录该内容

9 篇文章

订阅专栏

关于决策树，我一直不知道从哪里说起，后面专门去查阅了资料，才有了这篇文章，这里主要是介绍决策树的分类功能。如有不妥之处，还望指出。

决策树，决策树，首先他是树，那么在这里我先为大家简单介绍一下树的一些知识，如果想深入了解树的知识，大家可以去网上翻阅资料。

一、树

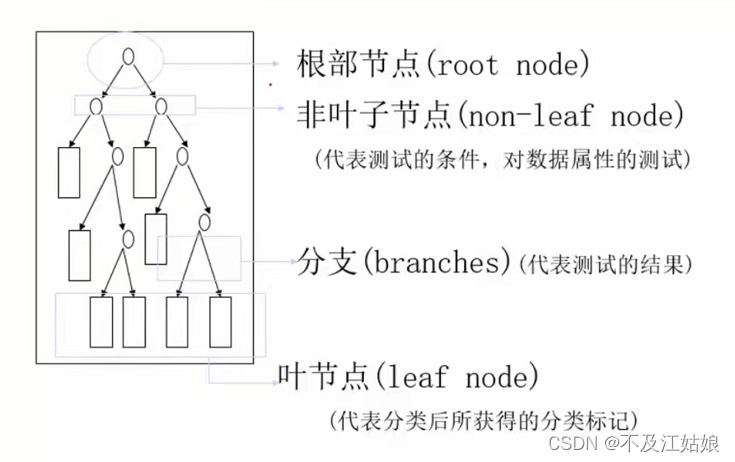
我们从这副图可以了解到。（分支我就不再叙述了，在图中它就是那一根根的线）根部节点它是同一棵树中除本身外所有结点的祖先，没有父结点。也就是说，他是第一个开始有分支的节点。非叶子节点，它是有分支的节点，但不是根节点。而叶子节点就是没有任何分支的节点，图中的长方形节点都是叶子节点。

二、案例引进决策树

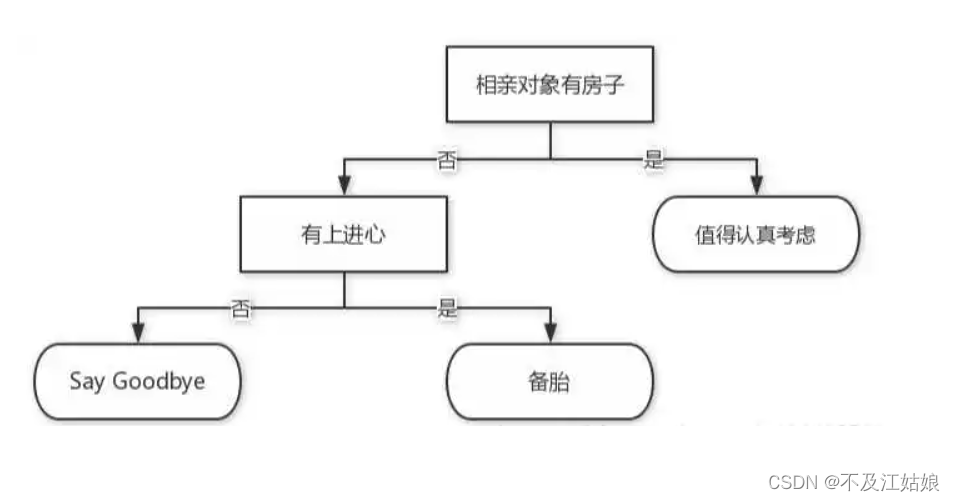
我们看到这个图，这颗树的目的是帮助你找对象。我们假设你找对象有两个标准，一个是有没有房子，一个是是否有上进心（这两个标准呢，用我们的话来说，叫特征值）。假设有5个找你处对象。而你对于上述两个标准，你最看重的是对方有没有房子，可不可以给你一个温软的家，所以首先来给他判断他是否有房子，有的话，那么他就非常符合你的条件，有3个人符合你的这个标准，我们就给这三个人分类到“值得认真考虑”，没有的话，你觉得他有可能是个潜力股，还是可以从里面挑选出优秀的对象的，也就是从第一个标准里淘汰的，任然还可以区分是否优秀，所以你用第二个标准，判断他是否有上进心，这个标准又可以把他分为两类，有1人有上进心，所有这1个人就是“备胎”，剩下1个人就是“Say Goodbye”这一类。总的来说，你就是靠着这两个标准，将相亲对象分为了3类。而你的这种分类方式，就是我要说的决策树。

从上面的引入案例，我们可以知道，决策树就是在每一个非叶子节点上定义一个标准，我们也管他叫决策属性，通过这些决策属性，我们只用将数据丢到决策树里，从上往下一走，它就可以将数据分成不同的类别，在决策树里，不同的类别由叶子节点表现。上述的例子从决策树的角度来说，就是丢进去5个数据，通过你规定的两个标准，将数据分为了“值得认真考虑”，“Say Goodbye”，和“备胎”三类，“值得认真考虑”这一类有3个数据，“Say Goodbye”和“备胎”这两类各有1个数据。

但还有一个问题，我怎么判断最重要的标准？在这个案例中，你知道哪一个是你最主要的标准，所以你拿这个标准做根节点，那在实际算法实现的过程中，我又要取哪一个作为最重要的标准，我又要取哪一个特征作为根节点呢，取到了根节点后，我又要拿哪一个特征作为接下来的次要标准，作为第二个节点呢？这，我们就绕不开决策树的一个核心——熵。

三、熵

熵，这个词我们通常是用在化学里面的，而它在化学里面的意义是物体内部分子混乱程度的度量，而我们这里的熵的意义也差不太多。我们在这里给大家具个例子：

例：假设我们有两个列表，每个列表里的数字代表不同的类别。

A = [1,1,1,2,4]
B = [1,2,3,5,6]

我们判断他们的“纯度”谁高谁低，B里面杂乱无章，里面有1，有2，有3等，那么我们就说这个B的“纯度”低，内部的混乱程度就比较高，也可以说它的熵值高，而A里面大部分都是1这个类别，我们就说它“纯度”比较高，那么它的内部混乱纯度就比较低，也就是它的熵值比较低。

了解了熵后，那我们怎么求熵呢？

$= -\sum_{i=1}^{n}p_{i}ln\left ( p_{i} \right )$

我们就是用这个公式来求的熵，这里的p指的是某个类别在数据中出现的概率值，比如上述的B中1类别出现的概率值就是1/5，而后面的ln(p)我们来看一下ln函数图像。

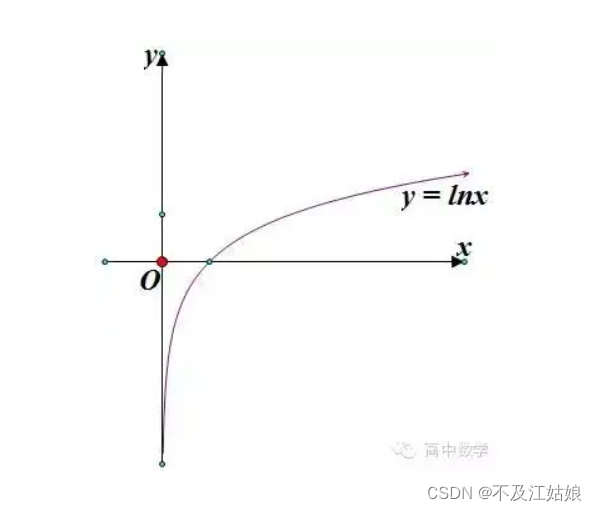
上述图像与X轴的交点是1。当ln(p)里面的p越小的时候，ln(p)负数就越小，那我们根据公式，在它前面加个负号，那如果p越小的话，-(p*ln(p))是不是就会越大，同样我们拿B列表举例，那么它的熵值是不是就等于5*（-p*ln(p))，那么它的熵值是不是就会很大啊，我们再假设一个C=[1,1,1,1,1]这个数据很“纯”吧，1类别出现的概率值p = 1，那我们再计算它的熵值，很容易得出等于0，那这不就说明它的熵值很低嘛。所以就是说，当一个数据里，它的类别越多，熵值就越大，反之，熵值就越小。

决策树的基本想法是随着树深度的增加，节点的熵迅速地降低。熵降低的速度越快越好，这样我们有望得到高度最矮的决策树,就是说如果一件事我可以三步做完，我肯定不愿意四步做完。这就是我们用熵来判断如何选择根节点的原理。下面我会用一个案例让大家更容易理解。

补充：

除了熵值，也可以用Gini系数，它的意义和作用和熵一样。Gini系数公式如下：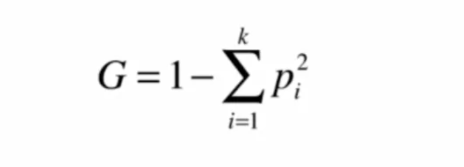

四、用熵判断根节点案例

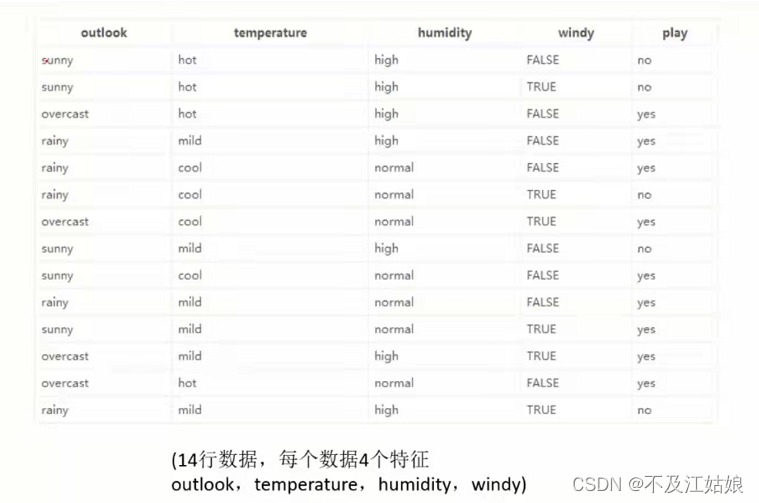
在这个图里，我们在四个条件的前提下，判断是否出去玩。这四个条件就是图上左边四列，分别是天气，温度，空气湿度，和是否有风。我们现在就要确定哪一个条件或者说是特征作为根节点。

我们根据构造树的基本想法，我们首先先来求一下没有任何特征时的熵值，或者说它什么都没做，自己固有的熵值是多少。从图中可以看出，在没有任何条件时，打球的概率是9/14，不打的概率是5/14。所以再根据熵值的计算公式，此时的熵值为：

$-\frac{9}{14}ln\frac{9}{14}-\frac{5}{14}ln\frac{5}{14}=0.940$

然后再我们将每一个特征进行划分，再分别对他们求熵值，如下：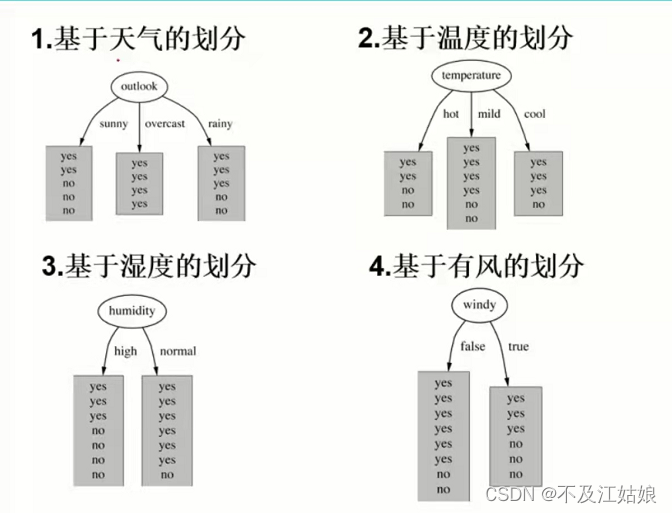

下面我们计算当已知变量outlook的值时，每个类的熵为多少：

outlook=sunny时，2/5的概率打球，3/5的概率不打球，熵值=0.971

outlook=overcast时，熵值=0

outlook=rainy时，熵值=0.971

再根据数据得出outlook取值为sunny，overcast，rainy的概率为别为5/14，4/14，5/14，所以当已知变量outlook的值时，熵为：

5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693

这样的话，熵值就从原先自己固有的熵0.940下降到了0.693，我们一开始说熵的意义是表示一个数据的混乱程度，而现在它下降了，所以就说明它混乱程度变低了。它们之间的差值为0.247，说明这个混乱程度降低了0.247，而这个差值，我们也叫它信息增溢。

以这样的方式，可以求出temperature特征下的信息增溢为0.029，humidity的信息增溢为0.152，windy的信息增溢为0.048。根据构造树的基本思想，outlook的信息增溢最大，所以我们决策树的根节点就取outlook。下一个节点的选取也是以此类推。

那我们就用信息增益这样的方式确定的决策树，一定就没有问题，没有bug吗？

显然是有的，我们还是那这个图举个例子，假如，我在这个数据列表的前面再加一列ID，就是序号，从上到下分别为1，2，3，4........14。很显然，我出不出去玩，和这一列的序号没有半毛钱的关系。那如果机器把这个序列号也当成了像outlook那样的特征，怎么办呢？

那这个时候，ID就有14个分支，我们来求1这个分支的熵，它等与-1 * ln(1) = 0，14个分支累加后的熵值还是等于0，那么它的信息增益就是0.940，这么大的一个信息增益，比outlook还大，所以我们就拿它当根节点？？？——答案肯定是否定的，那怎么解决这个问题呢？

解决这个问题，我们就得引入了一个新的概念——信息增益率。既然是率那肯定是一个比值的操作。我们继续以ID举例，从上面知道它的信息增益为0.940，那它的信息增益率就等于该信息增益比上它自身的熵值，它自身的信息增益就等于每一个分支熵的和，比如ID序列里的1的熵为-1/14 * ln(1/14)，2，3，4....14和1的熵一样，那么0.940比上它自身的熵值，数值就会很小。

所以我们不仅要算信息增益，还要求信息增益率。

好，现在我们已经可以根据熵构建一个决策树了。那我们怎么判断这棵决策树的好坏呢？？？——那就要用到评价函数了。

五、评价函数

$C\left ( T \right )=\sum_{t\epsilon leaf}N_{t}\cdot H\left ( t \right )$ (希望它越小越好，类似损失函数，如果不太了解损失函数，可以去看看我个人中心的KNN算法，里面有介绍）

函数里的t指的是每一个叶子节点，H(t)表示当前叶子节点的熵值，N(t)表示的是当前叶子节点里面样本的个数。

有了评价函数，我们就可以分析决策树的好坏了，那是不是说当一棵树很高的时候，高到每一个叶子节点的熵值都为零了，那这就能说明这棵决策树效果很好吗？？？——肯定不对，因为这样会发生过拟合(大家可以去csdn上搜索了解一下)，这样在训练集的训练效果会表现的很好，但是你把这个数据集“切”的太碎了，“切”的太碎肯定就会学到一些噪音点，错误点，这样的话，那在测试的过程中，效果就会不理想。所以有时候我们并不希望这棵树太高，那怎么解决这个问题呢？——高，就意味着分支多，所以我们要剪枝。

六、预剪枝和后剪枝

预剪枝：

在构建决策树的过程时，提前停止。

比如说，我现在定义一个参数表示树的高度，h=3，那么这棵树的高度到3它就停止了。或者我也可以设一个参数表示样本的个数，number<100，那么当一个节点的样本个数小于100的时候，它就停止了，不再生长了。

后剪枝：

决策树构建好后，再开始剪枝。

这种方法又得介绍一个函数：

$C_{\alpha }\left ( T \right )=C\left ( T \right )+\alpha \cdot \left | T_{leaf} \right |$ 这个公式用于当前节点，这里的C(T)就是我们前面所说的评价函数，T(leaf)是叶子节点的个数，阿拉法值是可以指定的，可大可小，当它大的时候，那么叶子节点就应该少一点，当它小的时候，就说加法明后面的式子对公式的影响比较小，那么叶子节点就可以多一点。根据他们的关系，创造了这个新的评价函数。叶子节点越多，损失越大，所以我们要取一个小的值（就是对比当前节点有叶子节点情况下的值和没有叶子节点情况的值，即本身就是一个叶子节点的时候）。