二分查找算法

二分查找算法

知识点

• 二分查找原理讲解
• 在单调递增序列 a 中查找 x 或 x 的后继
• 在单调递增序列 a 中查找 x 或 x 的前驱

二分查找算法讲解

枚举查找即顺序查找，实现原理是逐个比较数组 a[0:n-1] 中的元素，直到找到元素 x 或搜索整个数组后确定 x 不在其中。最坏情况下需要比较 N 次，时间复杂度是 O(n)，属于线性阶算法。

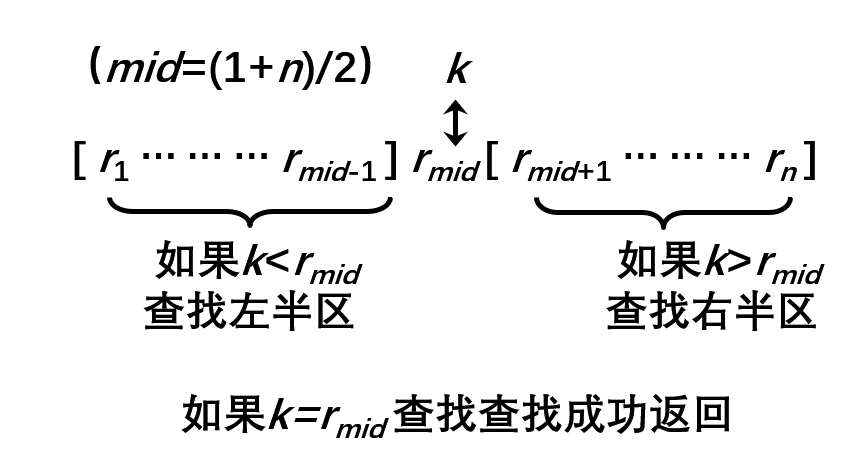
二分查找是一种折半查找方法。该方法将 N 个元素分成大致相等的两部分，选取中间元素与查找的元素进行比较。
如果相等，则查找成功；
如果查找元素小于中间元素，则在左半区继续查找；
如果查找元素大于中间元素，则在右半区继续查找。
半区指每次都将范围缩小至原来的一半，因此时间复杂度是 O(log2n)。
需要注意的是，二分查找的前提是数组有序，一般是从小到大排列。

折半查找的基本思想：

在有序表中（low, high, low<=high），取中间记录即 a[(high+low)/2] 作为比较对象。

• 若给定值与中间记录的关键码相等，则查找成功。
• 若给定值小于中间记录的关键码，则在中间记录的左半区继续查找。
• 若给定值大于中间记录的关键码，则在中间记录的右半区继续查找。

不断重复上述过程，直到查找成功或所查找的区域无记录，查找失败。

二分查找的特征：

1. 答案具有单调性。
2. 二分答案的问题往往有固定的问法，例如：令最大值最小（最小值最大），求满足条件的最大（小）值等。

折半查找一般过程：

下面是对文本的润色：

Step 1:
假设存在一个有序数组：
下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑                                                   ↑
    low=0                                              high=12

                    mid=(low+high)/2
                    mid=(0+12)/2
                    mid=6
                    [mid]=31 > 14，所以选择左半部分

操作：此时令low不变，high=mid-1=5

Step 2:
下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑                   ↑
   low=0                 high=5

                    mid=(low+high)/2
                    mid=(0+6)/2
                    mid=3
                    [mid]=21 > 14，所以选择左半部分

操作：此时令low不变，high=mid-1=2

Step 3:
下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]
      ↑       ↑
   low=0    high=2

                    mid=(low+high)/2
                    mid=(0+2)/2
                    mid=1
                    [mid]=14 = 14  找到答案

操作：返回下标

整数二分法常用算法模板

C++ 语言描述

// 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
while (low < high){
    int mid = (low + high) / 2;
    if (a[mid] >= x)high = mid;
    else low = mid + 1;
}

// 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）
while (low < high){
    int mid = (low + high + 1) / 2;
    if (a[mid] <= x)low = mid;
    else high = mid - 1;
}

为什么采用这一套代码的而不是采用查找等于的 X？

是因为这样的适用范围更广，当有 X 时这套代码就返回 X 的位置。
而重点是如果没有 X，就返回 <=x 的数中最大的一个或者 >=x 的数中最小的一个(最大值最小化，最小值最大化)。

分巧克力

2017 年省赛真题链接。

**题目描述:**小明一共有 N 块巧克力，其中第 i 块是Hi×Wi的方格组成的长方形。

小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足：

1. 形状是正方形，边长是整数;
2. 大小相同;

例如一块 6x5 的巧克力可以切出 6 块 2x2 的巧克力或者 2 块 3x3 的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入描述:

第一行包含两个整数 N*,K (1≤N*,K≤100000)。

以下 N 行每行包含两个整数Hi,Wi (1≤Hi,Wi≤100000)。

输入保证每位小朋友至少能获得一块 1x1 的巧克力。

输出描述:

输出切出的正方形巧克力最大可能的边长。

输入输出样例:

示例:

输入

2 10 6 5 5 6

输出

2

运行限制:

• 最大运行时间：2s
• 最大运行内存: 256M

题目分析

简单思路，边长的最大规模为 100000；我们可以枚举出所有的情况。按从大到小的顺序进行切割，直到找到满足要求的巧克力边长。

在判断边长是否满足条件时：求一块长方形（h∗w）最多被分成的正方形（len∗len）巧克力个数为：cnt=(h/len)∗(w/len)

但是使用朴素算法枚举时间复杂度O*(n)∗O(n)=O(n2) 会超时，所以改用 2 分查找法，这找到符合要求的最大的一个。

即用在单调递增序列 a 中查找 <=x 的数中最大的一个（即 x 或 x 的前驱）即可。

代码解答

C++ 实现：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=100010;
int n,k;
int h[MAXN],w[MAXN];
bool check(int l){
    int sum=0;
    for(int i=0; i<n; i++){
        sum+=(h[i]/l)*(w[i]/l);
        if(sum>=k)return true;
    }
    return false;
}

int main(){
    cin>>n>>k;
    for(int i=0; i<n; i++)cin>>h[i]>>w[i];

    //找到二分查找的上界
    int high=0;
    for(int i=0; i<n; i++){//查找上界其实可以直接输入的时候查询
        high=max(high,h[i]);
        high=max(high,w[i]);
    }
    
    // 二分下届由题意可得至少为1
    int low=1;
    
    // 由于本题目就是求符合要求的Mid 值所以要将mid定义在二分查找外边
    int mid=0;
    while(low<high){
        mid = (low + high+1) / 2;
        if(check(mid))low=mid;
        else high = mid - 1;
    }

    //因为low=high所以输出哪一个都一样
    cout<<low;
    return 0;
}

M 次方根

题目描述:

小 A 最近在学高等数学，他发现了一道题，求273327。现在已知，小 A 开始计算，11 的三次方得11，22 的三次方得88，33 的三次方得2727，然后他很高兴的填上了33。

接着他要求16455164。然后他开始11 的三次方得11，22 的三次方得88，33 的三次方得2727…

直到他算到了秃头，也没有找到答案。

这时一旁的小 B 看不下去了，说这题答案又不是个整数。小 A 震惊，原来如此。作为程序高手的小 A，打算设计一个程序用于求解 M 次根下N的值。

但是由于要考虑精度范围，答案必须要保留 77 位小数，连三次根号下2727都要掰手指的小 A 又怎么会设计呢。请你帮小 A 设计一个程序用于求解 M 次根号N。

数据范围：

1≤N≤1e5 1≤M≤100 且 M<N

要求输入:

输入描述:

第一行输入整数 N 和 M，数据间用空格隔开。

要求输出：

输出描述:
输出一个整数，并保留 7 位小数。

样例:

输入样例：
27 3
输出样例：
3.000000

运行限制:

最大运行时间：1s
最大运行内存: 256M

题目分析

根据前面的知识，我们要找到一个具有单调性的数列，去二分。
这个题的关键是我们要去二分什么，这里可以二分的是 a的M次方 中的 a，所以我们要先想办法设计出用于处理实数二分的代码。

这里两个模板，选择一个使用即可：

while (l + 精度+2< r)

for (int i = 0; i < 小于精度的log2循环次数; i++)

C++ 模版：

/*模版一：实数域二分，设置eps法
令 eps 为小于题目精度一个数即可。题目保留n位小数，则eps设置为n+1或n+2位小数的1-9即:	0.000...01到0.000...09
比如题目说保留4位小数，0.0001 这种的。那么 eps 就可以设置为五位或六位小数的任意一个数 0.00001- 0.00009 等等都可以。
一般为了保证精度我们选取精度/100即n+2位的那个小数，即设置 eps= 0.0001/100 =1e-6*/

double eps=1e-6;
while (l + eps < r){
    double mid = (l + r) / 2;
    if (check(mid))r = mid;
    else l = mid;
}

/*模版二：实数域二分，规定循环次数法
通过循环一定次数达到精度要求，这个一般 log2N < 精度即可。N 为循环次数，在不超过时间复杂度的情况下，可以选择给 N 乘一个系数使得精度更高。*/

for (int i = 0; i < 100; i++){
    double mid = (l + r) / 2;
    if (check(mid))r = mid;
    else l = mid;
}

模板讲完了，然后我们就要考虑判定条件了，怎样判定是否存在满足大于平均值的区间。

关于判定条件，我们应该设计一个代码用于比较 a**m* 和 N 的大小关系。

在我们代码中：

if (check(mid))r = mid;
else l = mid;

check成功的情况，一定是 check 的 mid 符合条件，且小于 mid 的一定符合条件。因此我们要在大于 mid 中继续查找，找到更大的 mid。

所以我们可以设计出如下判定条件:

double check(double a,int m){
    double c=1;
    while(m>0){
        c=c*a;
        m--;
    }
    if(c>=n)return true;
    else return false;
}

代码解答

C++ 实现：

#include <cstdio>
#include <iostream>
#include<iomanip> //用于浮点数输出
using namespace std;

double n,l,r,mid;
double eps=1e-8;

bool check(double a,int m){
    double c=1;
    while(m>0){
        c=c*a;
        m--;
    }
    if(c>=n)return true;
    else return false;
}

int main(){
    int m;cin>>n>>m;
//设置二分边界
    l=0,r=n;
//实数二分
    while (l + eps < r){
        double mid = (l + r) / 2;
        if (pd(mid,m))
            r = mid;
        else
            l = mid;
    }
    cout<<fixed<<setprecision(7)<<l;
    //一般使用print
    //printf("%x.yf",n)
    //其中X是固定整数长度，小数点前的整数位数不够，会在前面补0
    //y是保留小数位数，不够补零
    //printf("%.7f",l);
    return 0;
}

总结

二分的题目主要是必须要求是单调的，一般会有条件等字眼。
做这种题目主要还是找到递增或者递减的序列，然后关于序列的判定条件。
或者通过观察时间复杂度来看是否可以使用二分。