KMP算法

  近期在看KMP算法，感觉好难懂，所以在这里简单整理一下，供大家参考。

什么是KMP算法？

  KMP算法是由Knuth，Morris和Pratt三位大佬发明的，所以由三位大佬的名字首字母命名。
  KMP算法主要是为了解决查找子字符串的一类问题。比如说有两个字符串S和T，S = "aabaac"，T = "aabaabaac"，我们想要查找字符串T中字符串S出现的位置，即可用KMP算法。当然，在Java中我们可以直接调用indexOf()方法。
  在这里字符串S称为模式串，字符串T称为文本串。

KMP的优势

  假设字符串S的长度为m，字符串T的长度为n。对于普通的暴力解法来说，时间复杂度为$O(m\ast n)$，然而KMP的时间复杂度为$O(m+n)$。KMP比暴力匹配快的关键在于，KMP能够利用之前匹配的的信息，来跳过一些不可能的情况。

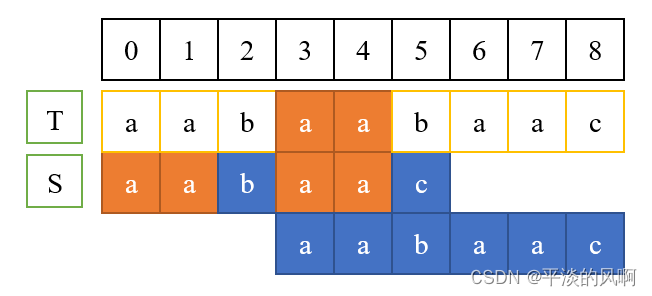
  我们从第一个字符开始，逐字符进行比较，我们发现S[0]~S[4]与T[0]~T[4]是匹配的，S[5]和T[5]不匹配，在匹配成功的部分中，存在相等的前缀和后缀，即图中橙色的部分，T[3~4]和S[3~4]相等，而S[3~4]和S[0~1]相等，T[3~4]和S[0~1]也是相等的。那么所以说我们不必从头开始重新进行匹配，只需要从S[2]和T[5]这里开始继续匹配就ok了。
  这样一来，省去了很多无效的匹配，从而提高了效率。

前缀表及其计算

  在刚刚的例子中，我们提到了当遇到不匹配的字符时，利用相等的前后缀去查找下一次匹配的位置。
  首先看一下什么是前缀和后缀：
  前缀：指以字符串的第一个字符开始，但不包括最后一个字符的子字符串。例如，aabaac的前缀有a、aa、aab、aaba、aabaa。
  后缀：指以字符串的最后一个字符为结尾，但不包括第一个字符的子字符串。例如，aabaac的后缀有c、ac、aac、baac、abaac。
  最长公共前后缀：指一个字符串中最长的相等的前缀和后缀。比如aabaa的最长公共前后缀为aa，长度为2。
  那么什么是前缀表？前缀表记录字符串的下标i之前（包括i）的子字符串中，最长公共前后缀的长度是多少。我们用next[]数组来表示前缀表。

  仍以S = "aabaac"为例，我们想要计算next[4]，我们发现在索引为4之前的子字符串中（即S[0~4]），最长的公共前后缀为aa，长度为2，所以说next[4]=2。
  再来解释一下为什么需要前缀表？首先前缀表记录了字符串S中每个索引i（包括i）之前的子字符串的最长公共前后缀的长度；然后以上面的例子来说明，在S的索引i=5处，匹配失败，而S和T的索引0~4位置的字符是匹配成功的，匹配失败的位置在S、T的后缀的后面，T的后缀和S的前缀又是相等的，所以只需要从S的前缀的后面一个字符和T的后缀的后一个字符继续匹配就OK了，即S[2]和T[5]。

前缀表next的计算

  首先，next[suffix]定义为字符串S的子字符串S[0~suffix]的最长公共前后缀的长度。可以用递推的方式来求next数组，我们假设已知next[0]~next[suffix-1]，要计算next[suffix]。
  记prefix = next[suffix-1]，即prefix为S[0~suffix-1]的最长公共前后缀的长度，那么prefix指向S[0~suffix-1]的最长公共前后缀的前缀的下一个索引位置。看图：

  下面可以分为两种情况：
  第一种情况：S[suffix] == S[prefix]，那最长相等前后缀的长度就可以扩展一位，于是next[suffix] = prefix + 1，就像上图所示，next[4] = 1+1 = 2；
  第二种情况：S[suffix] != S[prefix]，如下图：

  这个时候S[suffix] != S[prefix]，我们应该尝试着去缩小prefix，使得S[0~suffix-1]中prefix长度的前缀和后缀仍然相等，这个时候再去比较S[suffix]和S[prefix]是否相等。即下图：

  如果S[suffix] == S[prefix]，那么就可以计算next[suffix] = prefix + 1；如果不等，那么可以继续重复前面的步骤，直到S[suffix] == S[prefix]，或者prefix等于0。
  现在的问题是，该如何计算prefix？我们把S[0~suffix-1]的最长公共前后缀的前缀记为字符串A，后缀记为字符串B，那么首先A是等于B的，我们要找的是一个最长的的prefix使得S的前缀和后缀相等，并且要求S[suffix] == S[prefix]，这个前缀一定在A内部，后缀一定在B内部。而由于A等于B，所以A的后缀等于B的后缀，所以只需要找到A的最长公共前后缀就可以了！即prefix = next[prefix - 1]，一直按此向前查找，直到S[suffix] == S[prefix]或者prefix == 0。
  至此，我们找到了前缀表，接下来只要按照前缀表去查找就可以了。

KMP的代码实现：

  下面附上完整代码：

class Solution {
    public int strStr(String haystack, String needle) {
        if(needle.isEmpty()){
            return 0;
        }
        int j = 0;
        int[] next = new int[needle.length()];
        getNext(next, needle);
        for(int i = 0; i < haystack.length(); i++){
            while(j > 0 && haystack.charAt(i) != needle.charAt(j)){
                    j = next[j - 1];
            }
            if(haystack.charAt(i) == needle.charAt(j)){
                j++;
            }
            if(j == needle.length()){
                return i - j + 1;
            }
        }
        return -1;
    }
    public void getNext(int[] next, String s){
        int prefix = 0;
        next[0] = 0;
        for(int suffix = 1; suffix < s.length(); suffix++){
            if(s.charAt(suffix) == s.charAt(prefix)){
                prefix++;
                next[suffix] = prefix;
            }else{
                while(prefix > 0 && s.charAt(suffix) != s.charAt(prefix)){
                    prefix = next[prefix - 1];
                }
                if(s.charAt(suffix) == s.charAt(prefix)){
                    prefix++;
                }
                next[suffix] = prefix;
            }
        }
    }
}