《剑指offer》07.重建二叉树

重建二叉树

LeetCode：剑指offer 07.重建二叉树

输入某二叉树前序遍历和中序遍历的结果，请重建该二叉树，假设输入的前序遍历和中序遍历的结果都不含重复的数字

示例：

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下二叉树：

    3
   / \
  9  20
    /  \
   15   7

二叉树的节点定义如下：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

题目考点

• 考察应聘者对二叉树的前序遍历和中序遍历的理解程序。只有对二叉树的不同遍历算法有了深刻的理解，应聘者才有可能在遍历序列汇总划分出左、右子数对应的子序列。
• 考察应聘者分析复杂问题的能力。我们把构建二叉树的大问题分解成构建左、右子树的两个小问题。我们发现小问题和大问题在本质上是一致的，因此可以用递归的方式解决

解题思路：

前序遍历的第一个值为根节点的值，使用这个值将中序遍历结果分成两部分，左部分为树的左子树中序遍历结果，右部分为树的右子树中序遍历的结果。接下来的事情我们就可以用 递归 的方法完成了。

前序遍历性质： 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。
中序遍历性质： 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。

根据以上性质，可得出以下推论：

• 前序遍历的首元素 为 树的根节点 node 的值。
• 在中序遍历中搜索根节点 node 的索引 ，可将 中序遍历 划分为[ 左子树 | 根节点 | 右子树 ]
• 根据中序遍历中的左 / 右子树的节点数量，可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ]

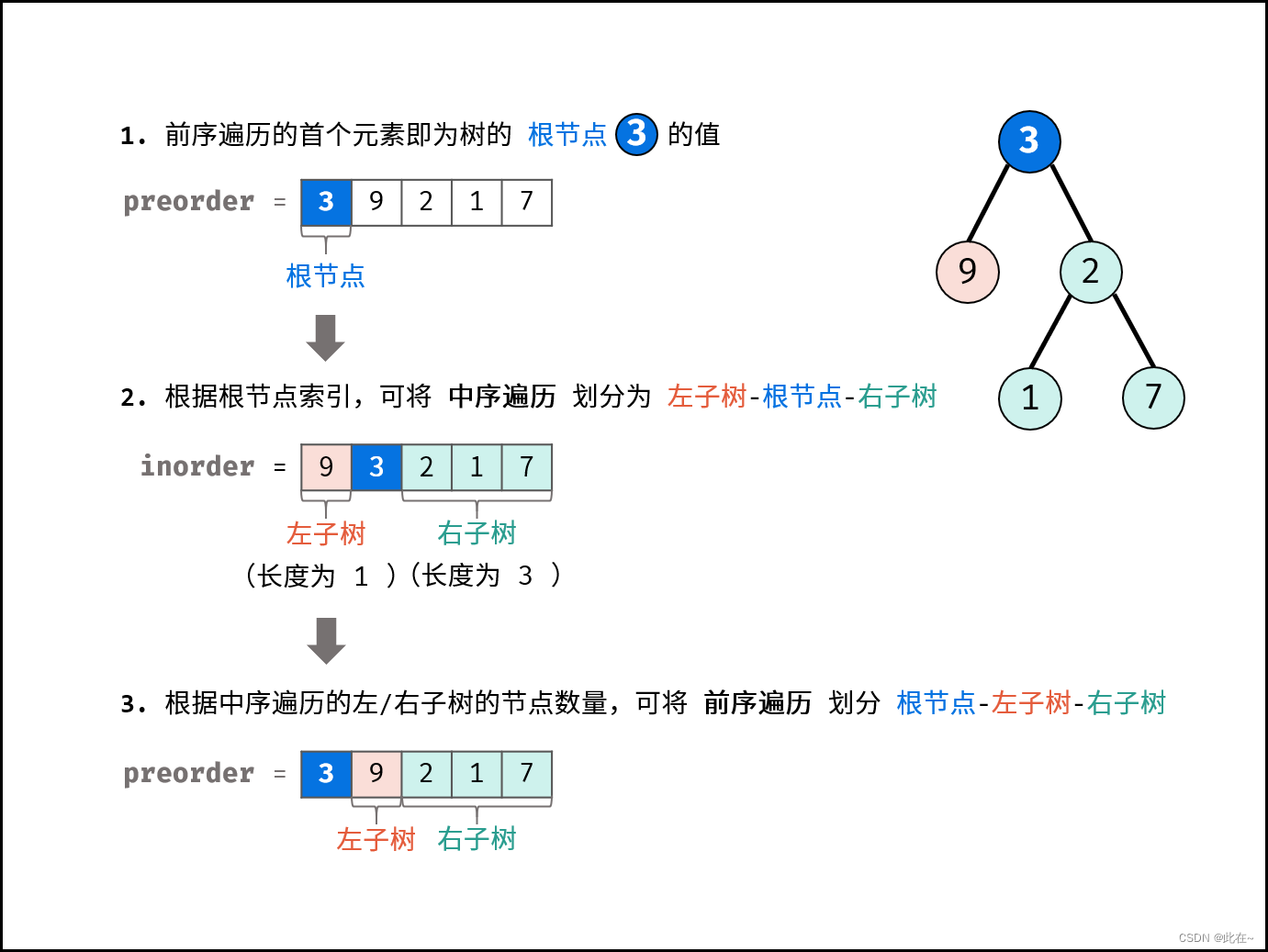
通过以上三步，可确定 三个节点 ：1.树的根节点、2.左子树根节点、3.右子树根节点。
对于树的左、右子树，仍可使用以上步骤划分子树的左右子树。

以上子树的递推性质是通过分治算法来实现的，通过递归对所有子树进行
划分

代码示例：

    public int preIndex = 0;//保证每次递归时不会被重新赋值为0
    public TreeNode buildTreeChild(int[] preorder ,int[] inorder,int inbegin,int inend) {
        if(inbegin > inend) {//递归的终止条件
            return null; //此时节点 没有 左树 或者 没有右树
        }
        TreeNode root = new TreeNode(preorder[preIndex]);
        //通过前序遍历找到在中序遍历中根节点的位置
        //并以此为界限进行分治递归
        int rootIndex = findInorderIndex(inorder,inbegin,inend,preorder[preIndex]);
        preIndex++;//前序遍历 根左右，根的值往后移一位
        //建左右子树，注意左子树与右子树遍历时参数不同
        root.left = buildTreeChild(preorder ,inorder,inbegin,rootIndex-1);
        root.right = buildTreeChild(preorder ,inorder,rootIndex+1,inend);
        //建树完毕，返回
        return root;
    }

    public int findInorderIndex(int[] inorder,int inbegin,int inend,int key) {
        for(int i = inbegin;i <= inend;i++) {//找到在中序遍历中的位置
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || inorder == null) return null;
        return buildTreeChild(preorder, inorder,0,inorder.length-1);
    }

参考内容1

参考内容2