剑指offer- 07 重建二叉树

根据前序遍历和后序遍历创建二叉树

题目链接：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/

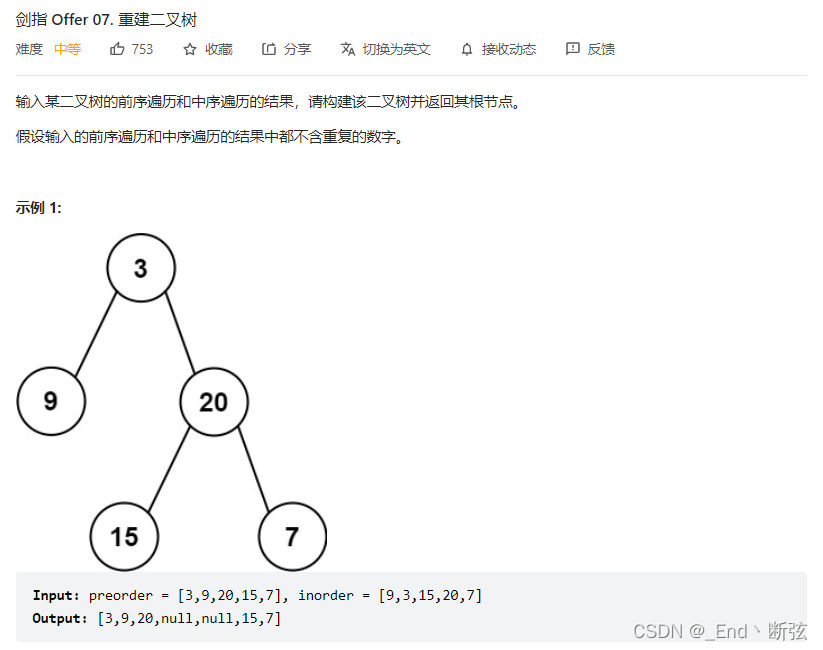
二叉树的前序遍历是：根 、左子树、右子树
中序遍历是： 左子树 、根、右子树
例：二叉树的前序遍历：1, 2，4, 7，3, 5，6, 8
二叉树的中序遍历： 4, 7，2, 1，5, 3，8, 6
思想是递归分制，前序确定根，中序确定左右子树，再在确定好的左右子树区间内，前序确定根，中序确定左右子树的区间

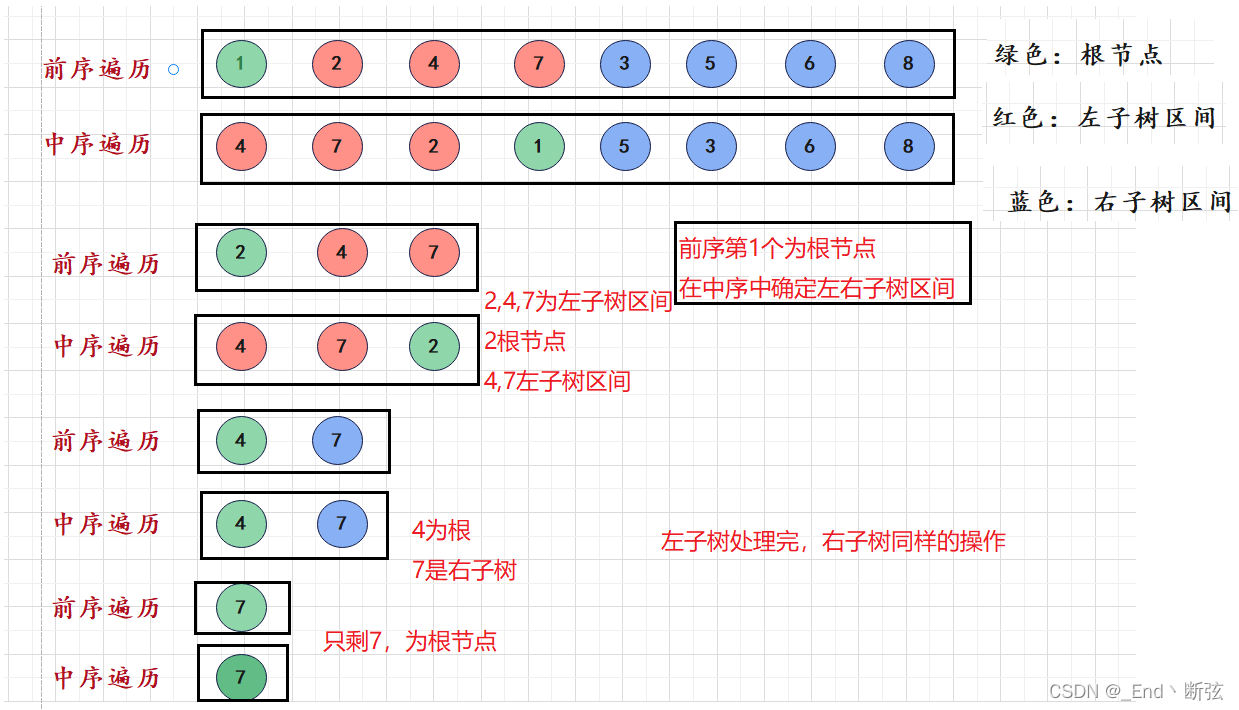
递归步骤：

• 递推参数：前序遍历，中序遍历，左子树在前序遍历中的左边界，左子树在前序遍历中的右边界，左子树在中序遍历中的左边界，左子树在中序序遍历中的右边界
• 终止条件：左边界大于右边界
• 递推工作：
  1.建立根节点
  2.划分左右子树
  3.构建左右子树
  为了不用遍历中序来找根节点，可以用哈希表来存中序遍历的值和索引的映射，哈希表的查找时间为O(1)

画图确定左右子树的区间：

代码如下：

class Solution {
    private:
         unordered_map<int, int> hash;  
   
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
         
    for(int i = 0; i < inorder.size();++i)
    {
        hash[inorder[i]] = i;//用哈希表保存中序遍历
    }
    return dfs(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
}
TreeNode* dfs(const vector<int>&preorder,const vector<int> inorder,int pl,int pr,int il,int ir)
{
   if(pl > pr)   //递归结束出口
   return nullptr;
    TreeNode* root = new TreeNode(preorder[pl]);//先构建根节点
     
    int index = hash[preorder[pl]];     //根节点的位置
    int leftSize = index - il;        //左子树的个数
    root->left = dfs(preorder,inorder,pl+1,pl+leftSize,il,index -1);//先重建左子树,区间根据图
    root->right = dfs(preorder,inorder,pl+leftSize+1,pr,index+1,ir);//再重建右子树
    return root; 
}

};

复杂度：
时间复杂度：O(n)其中 n是树中的节点个数。

空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，还需要使用 O(n) 的哈希，以及 O(h)（其中 h是树的高度）的空间表示递归时栈空间。这里 h < n，所以总空间复杂度为 O(n)。

根据中序遍历和后序遍历创建二叉树

题目链接：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

后序遍历:左子树、右子树、根节点
中序遍历：左子树、根节点、右子树

上面的是根据前序和中序创建二叉树，下面的是根据中序和后序遍历创建二叉树。
还是一样的处理方法。
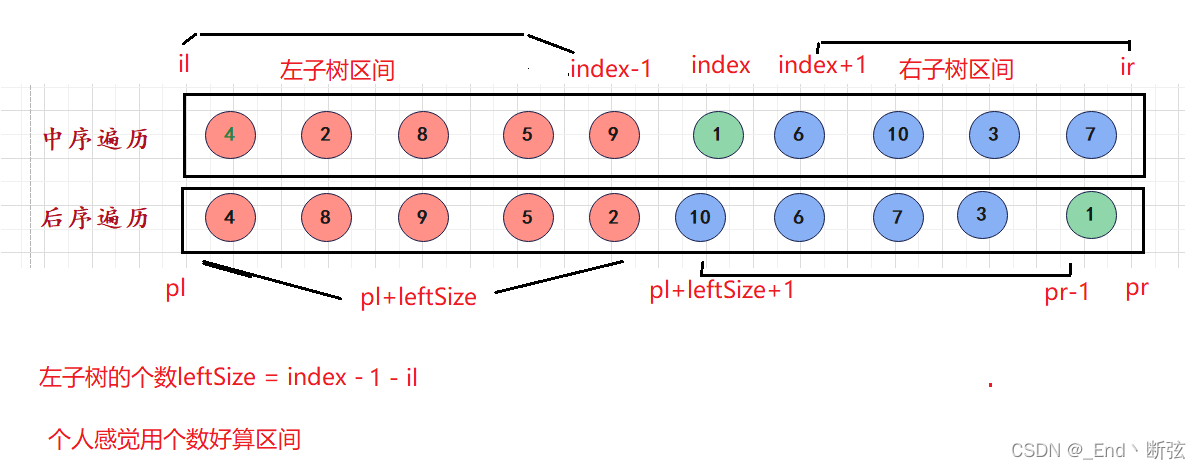
画图：

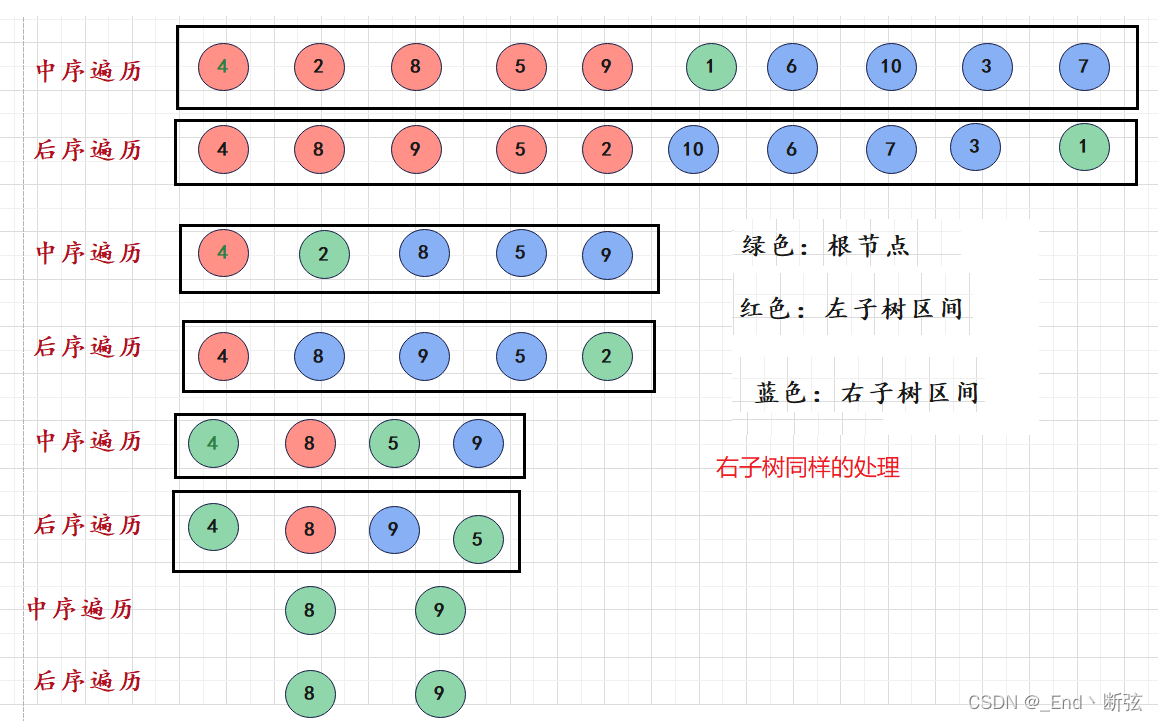
中序遍历好事用哈希表存一下，查找根节点很快
区间计算：

代码如下：

class Solution {
    private:
    unordered_map<int, int> hash;  
public:

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        for(int i = 0;i < inorder.size();++i){
            hash[inorder[i]] = i;  //用哈希表记录中序遍历
        }
        return dfs(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);
    }
    TreeNode* dfs(vector<int>& inorder, vector<int>& postorder,int il,int ir,int pl,int pr){
        if(il > ir)
        return nullptr; //递归结束
        
        TreeNode* root = new TreeNode(postorder[pr]);//根节点是后序的最后一个
        
         int index = hash[postorder[pr]];//根节点位置
         int leftSize = index - il - 1;  //计算出左子树的个数
        root->left = dfs(inorder,postorder, il,index-1,pl,pl+leftSize);//先递归左子树
        root->right = dfs(inorder,postorder,index+1,ir,pl+leftSize+1,pr-1);//再递归右子树
        return root;

    }
};

复杂度：
时间复杂度：O(N)
空间复杂度：O(N),额外的使用了哈希表

这2个题的细节就是处理左右子树的区间问题。博主没有研究迭代的方法处理这2个题。