牛客小白月赛39 (题解报告）

最新推荐文章于 2024-09-21 10:59:26 发布

原创最新推荐文章于 2024-09-21 10:59:26 发布 · 681 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

牛客题解报告专栏收录该内容

5 篇文章

订阅专栏

本文介绍了ACM/NOI/CSP等算法编程比赛的若干题目，包括暴力枚举、字符串处理、模拟算法和贪心策略等。针对每个题目，提供了简洁的解题思路和代码实现，涉及数据结构与算法的应用。

题目地址：

牛客小白月赛39_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

A-憧憬

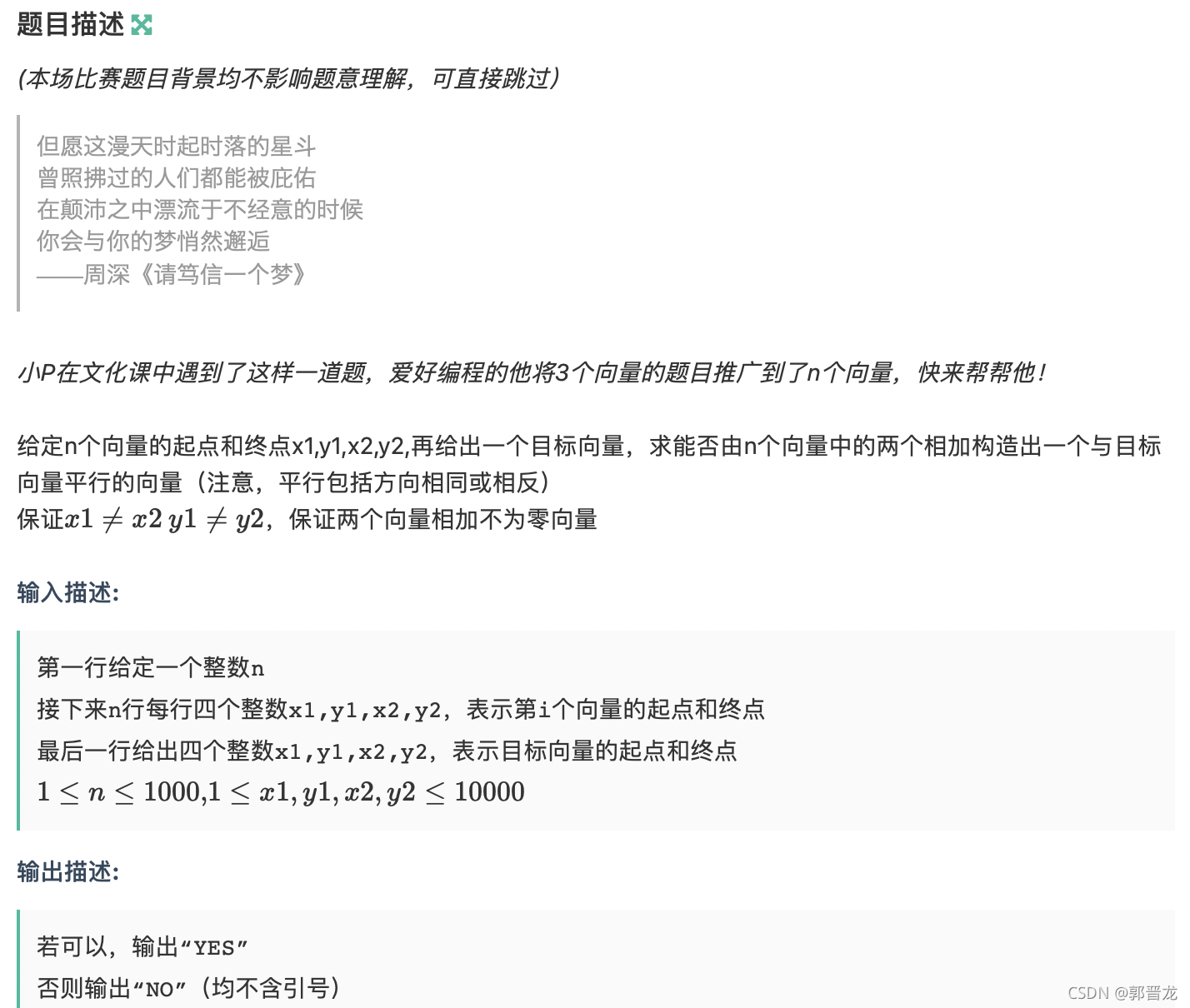
简单的暴力枚举O(n^2)就行

判断向量平行就行x1y2==x2y1

const int MAX=100010;
int yy[MAX];
int xx[MAX];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        xx[i]=x2-x1;
        yy[i]=y2-y1;
    }
    int x1,y1,x2,y2;
    cin>>x1>>y1>>x2>>y2;
    int xb=x2-x1;
    int yb=y2-y1;
//    cout<<"xb="<<xb<<endl;
//    cout<<"yb="<<yb<<endl;
    for(int i=0;i<n;i++){
        for(int j=i+1;j<n;j++){
            int x=xx[i]+xx[j];
            int y=yy[i]+yy[j];
//            cout<<"x="<<x<<endl;
//            cout<<"y="<<y<<endl;
            if(x*yb==y*xb){
                cout<<"YES"<<endl;
                return 0;
            }
        }
    }
    cout<<"NO"<<endl;
}

B-欢欣

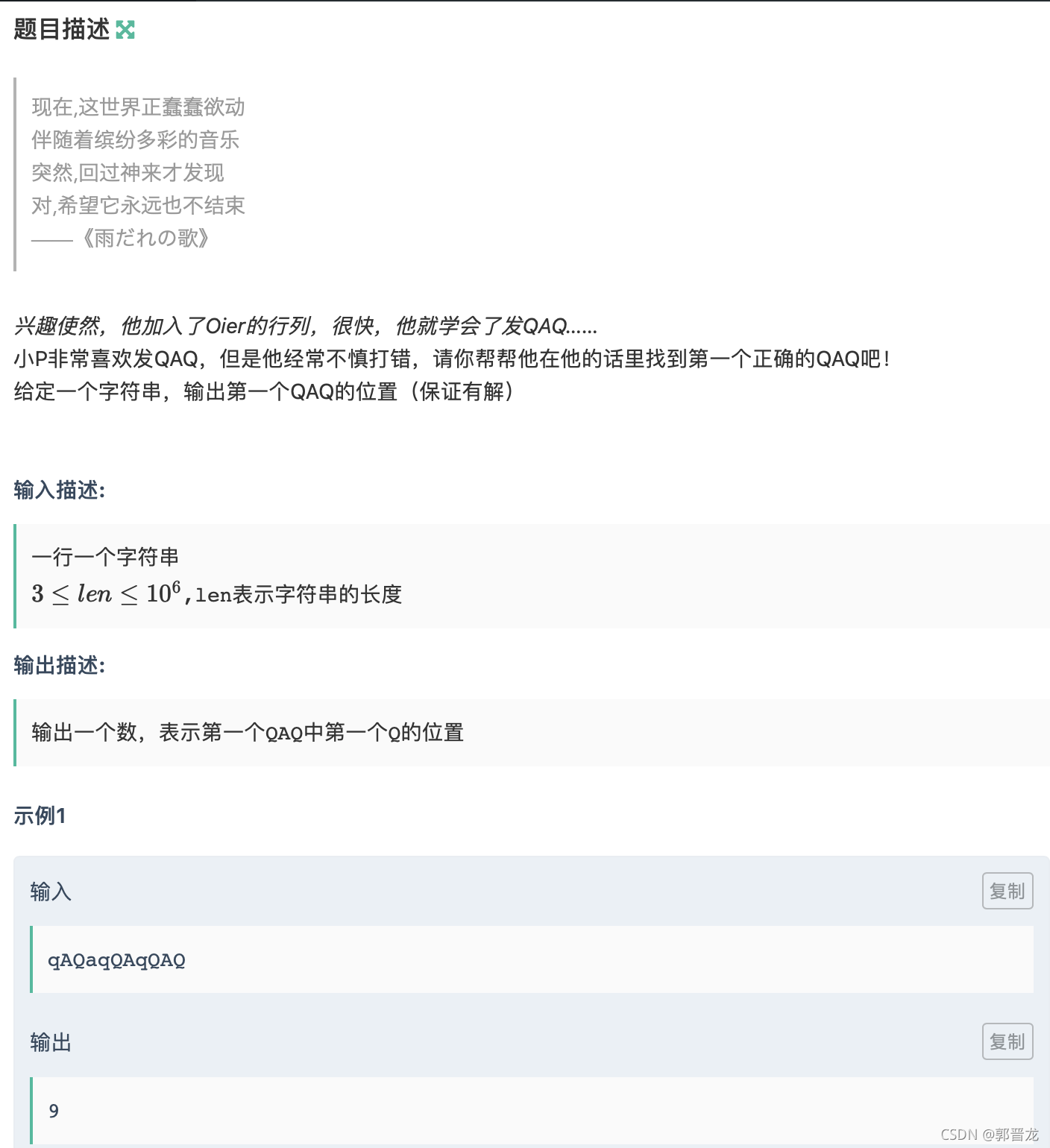
简单的字符串处理可以直接模拟也可以借助STL的string方式进行处理

const int MAX=10000010;
string s;
int main(){
    cin>>s;
    for(int i=0;i<s.size();i++){
        if(s[i]=='Q'&&s[i+1]=='A'&&s[i+2]=='Q')
        {
            cout<<i+1;
            break;
        }
    }
}

C-奋发

D-绝望

E-迷惘

简单的模拟题：

1.先把数转化为二进制整数

2.然后去掉前导零

3.转化为十进制相加即可

int main(){
    int n;
    cin>>n;
    ll ans=0;
    for(int i=0;i<n;i++){
        ll a;
        cin>>a;
        string s;
        s=work(a,2);
        reverse(s.begin(),s.end());
        string ss;
        int id;
        for(int j=0;j<s.size();j++){
            if(s[j]!='0')
            {
                id=j;
                break;
            }
        }
        for(int j=id;j<s.size();j++){
            ss+=s[j];
        }
//        cout<<"this is string "<<ss<<endl;
        ll num=0;
        for(int j=0;j<ss.size();j++){
//            cout<<j<<" "<<ss[j]<<endl;
            num+=(ss[j]-'0')*pow(2,ss.size()-1-j);
        }
//        cout<<"this is num"<<num;
        ans+=num;
    }
    cout<<ans<<endl;
}

F-孤独

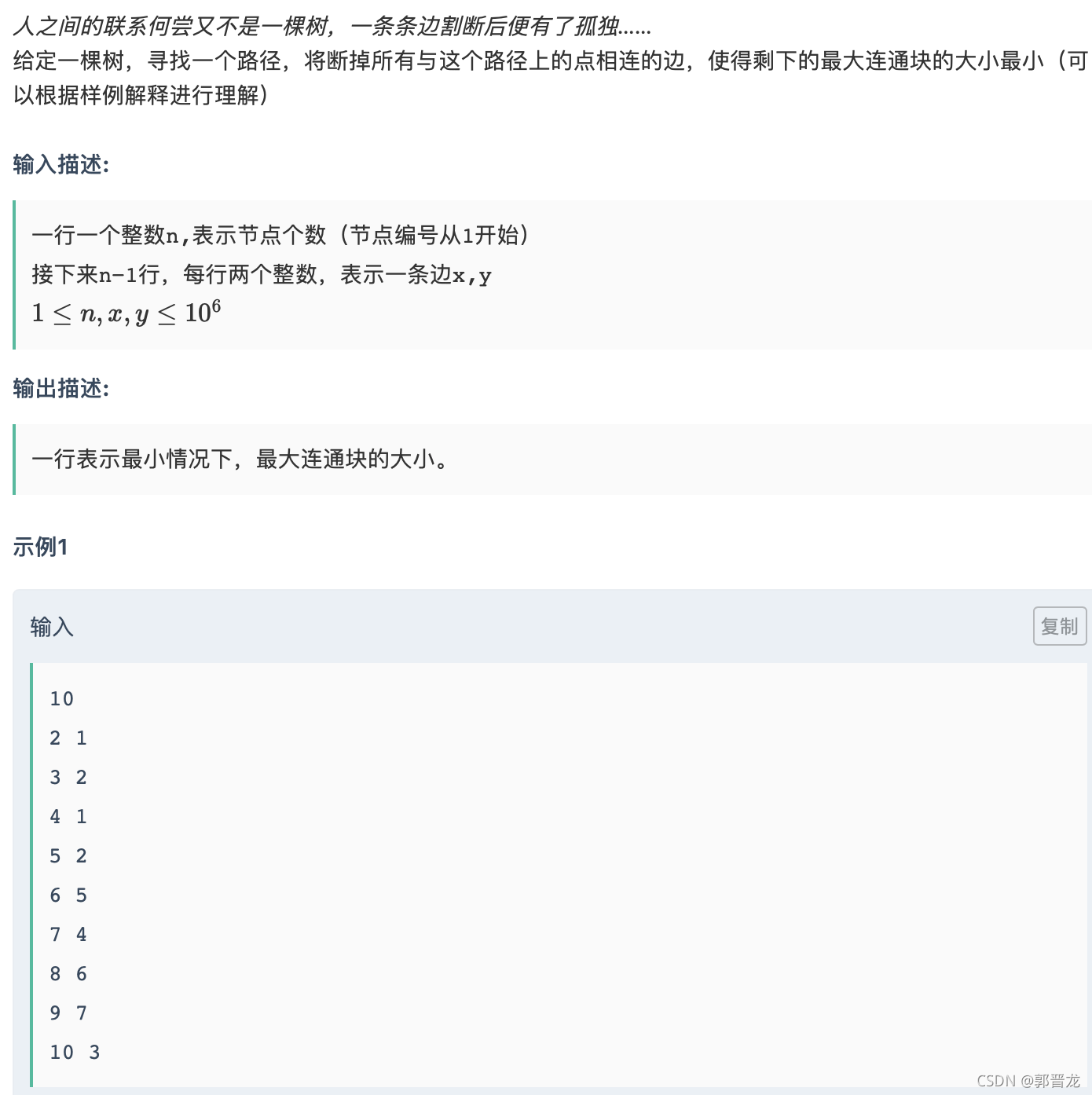
G-冷静

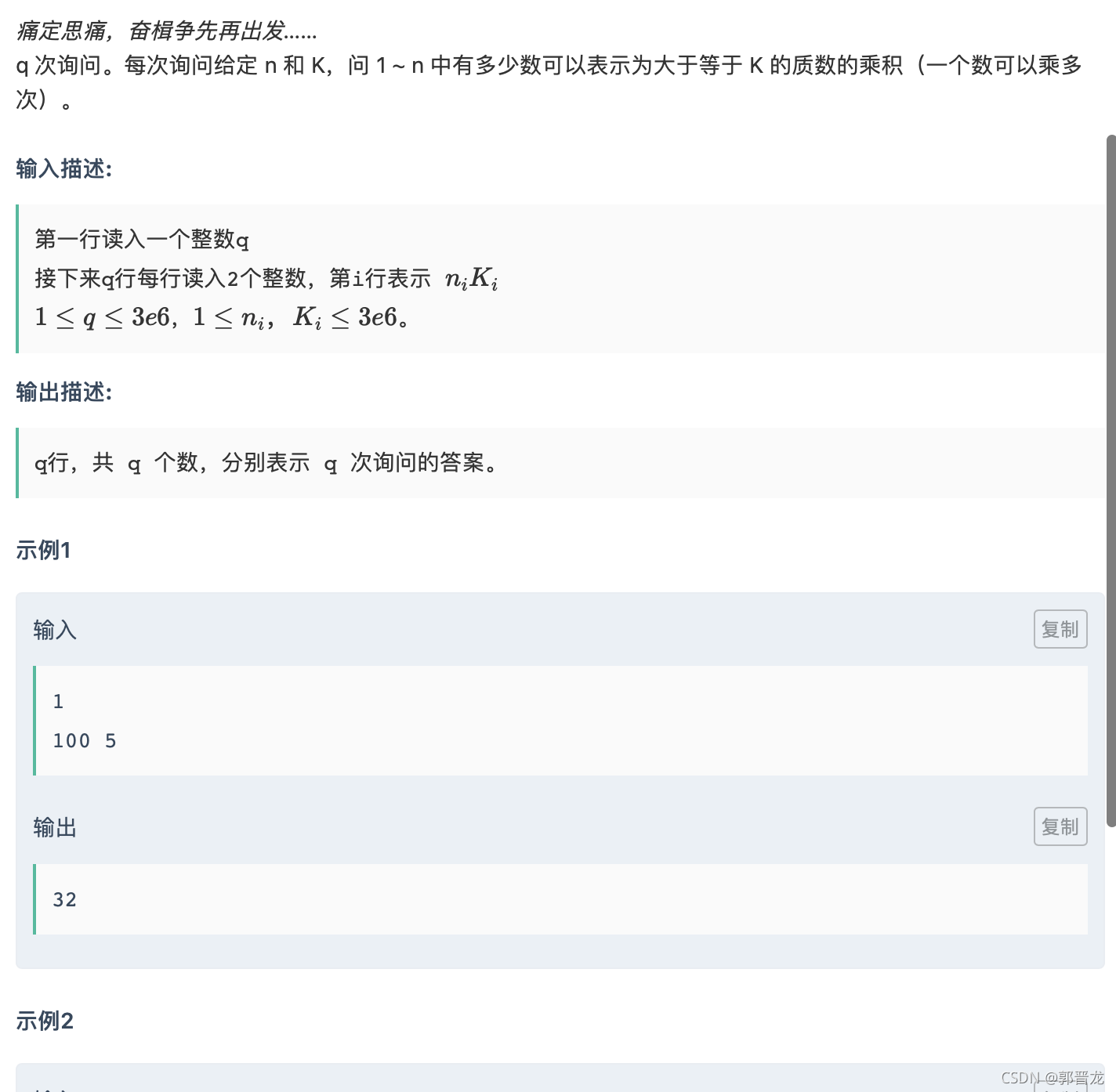
其实题意就是找出1-n最小质因数大于等于k的数的个数

我们可以开一个树状数组从小到大加入每个数的最小质因数

然后询问即可

我们先预处理每个数的最小质因数

然后

const int MAX=3e6+5;


// bitset<N> v;
ll v[MAX];
ll p[MAX];
ll cnt = 0;
void init(int n)
{
    for (int i = 2; i <= n; i++){
        if (v[i]==0) {
            p[++cnt] = i;
            v[i] = i;
        }
        for (int j = 1; j <= cnt; j++){
            if(p[j] > v[i] || p[j] > n / i)break;
            v[i * p[j]] = p[j];
        }
    }
}


struct node {
    ll r,k;
    ll pos;
    bool operator <(const node &p)const{
        return r<p.r;
    }
}a[MAX];
ll c[MAX];
ll lowbit(int x){
    return x&(-x);
}
void add(int x,int val){
    while (x<MAX) {
        c[x]+=val;
        x+=lowbit(x);
    }
}
ll query(int x){
    ll ans=0;
    while (x) {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
ll ans[MAX];
int q;
signed main(){
    cin>>q;
    for(int i=1;i<=q;i++){
        a[i].r=read();
        a[i].k=read();
        a[i].pos=i;
    }
    sort(a+1,a+1+q);
    init(MAX);
    int now=2;
    for(int i=1;i<=q;i++){
        while (now<=a[i].r) {
            add(v[now],1);
            now++;
        }
        ans[a[i].pos]=query(a[i].r)-query(a[i].k-1);
    }
    for(int i=1;i<=q;i++)
        printf("%lld\n",ans[i]);
}

H-终别

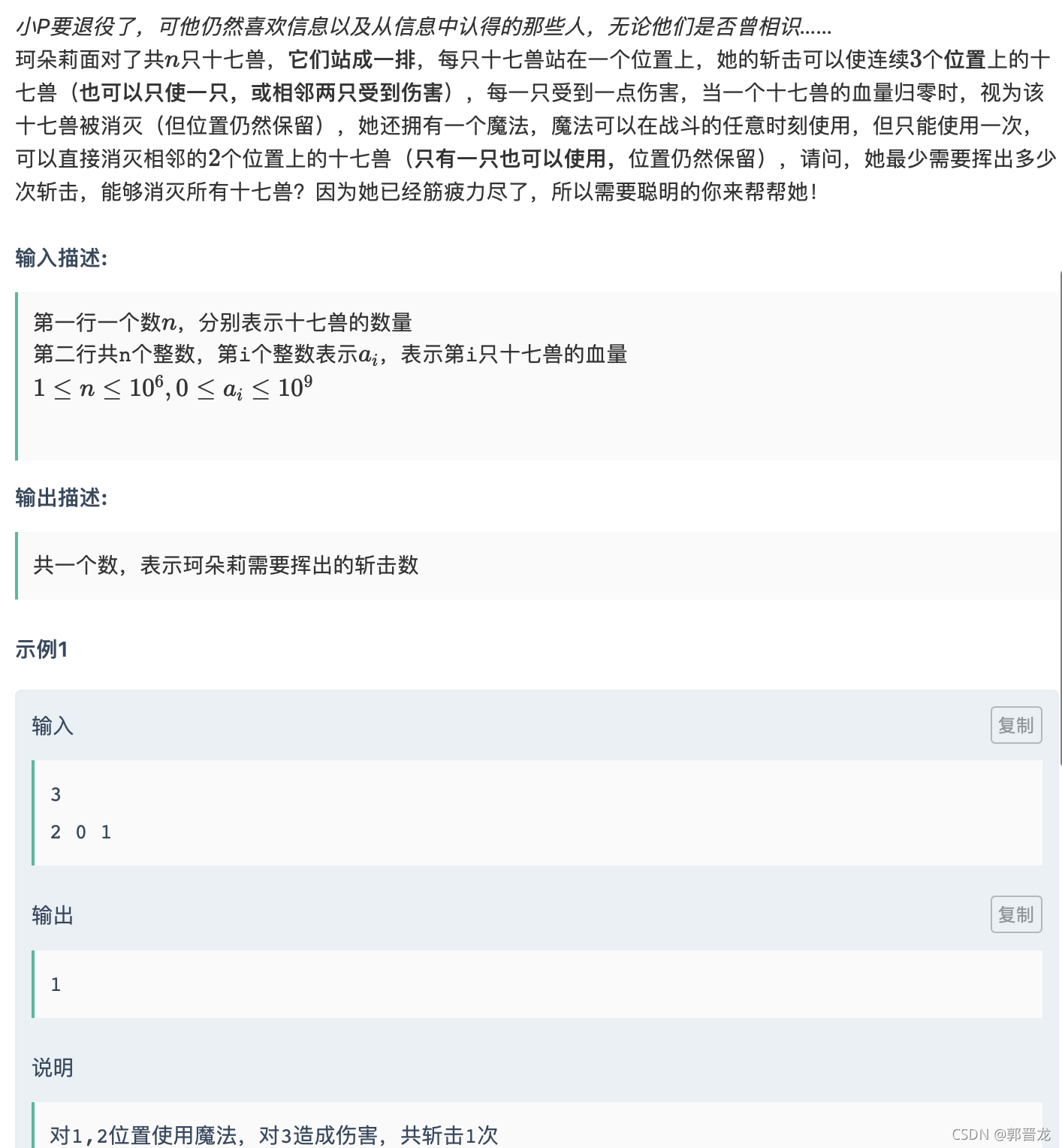
贪心：

如果不使用魔法的话直接从左到右依次处理即可

显然同时处理三个要比一个一个处理要好

如果第i个之前的都处理完了

那么我们就要同时处理第i,i+1,i+2个直到第i个被处理完

若是使用魔法的话我们可以枚举使用魔法的位置

我们可以预处理l r数组

l r数组是前l后r所有被消灭完所需要的处理的次数

使用最后的时间复杂度是O(n)

const int MAX=1e6+10;
ll l[MAX],r[MAX];
ll a[MAX];
ll b[MAX];
int n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=a[i];
    }
    for(int i=2;i<=n+1;i++){
        l[i]=l[i-1]+a[i-1];
        a[i]=max(0,a[i]-a[i-1]);
        a[i+1]=max(0,a[i+1]-a[i-1]);
    }
    for(int i=n-1;i>=0;i--){
        r[i]=r[i+1]+b[i+1];
        b[i]=max(0,b[i]-b[i+1]);
        b[max(i-1,0)]=max(0,b[max(0,i-1)]-b[i+1]);
    }
    ll ans=1e15;
    for(int i=1;i<n;i++){
        ans=min(ans,l[i]+r[i+1]);
    }
    cout<<ans;
}