红黑树知识总结

红黑树

红黑树是不严格的平衡二叉树
红黑树只是二叉查找树，不是平衡二叉树。“红黑树在最差情况下，最长的路径都不会比最短的路径长出两倍。其实红黑树并不是真正的平衡二叉树，它只能保证大致是平衡的，因为红黑树的高度不会无限增高，在实际应用用，红黑树的统计性能要高于平衡二叉树，但极端性能略差。”

一、红黑树的特点:

1.每个节点不是黑色就是红色

2.根节点永远是黑色

3.叶子节点是null节点,且颜色是黑的

4.当一个节点是红色的,那么它的子节点必须是黑色的

5.一个节点的所有子孙节点到该节点的所有路径上包含相同数目的黑色节点

注：可以通过下图把每个特点理解一下

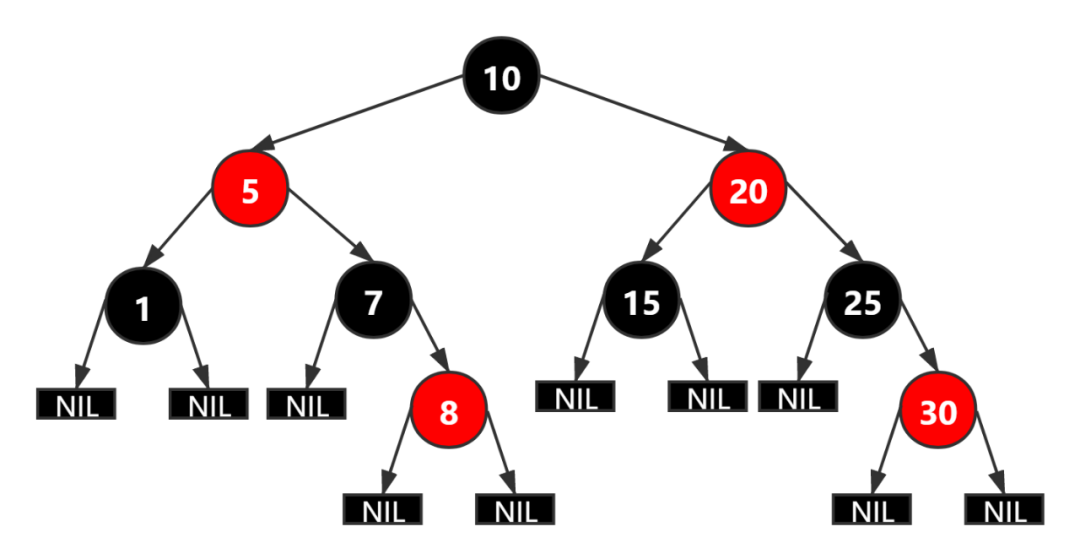
3、红黑树的自我修正

红黑树通过三种方式进行自我修正：改变节点颜色、左旋转和右旋转。

我们在插入结点时，要插入红色节点，因为相对黑色节点来说，插入红色节点需要变化的可能性比较小，修正的代价也比较小。

我们在下面这棵红黑树上插入6这个结点

改变节点颜色

• 如果当前结点的父节点是红色，且祖父节点的另外一个子节点(即叔叔结点)也为红色

• 把父节点和叔叔结点置为黑色

• 把祖父结点置为红色

• 最后把指针指向祖父节点，分析祖父节点将要变换的原则(指向 8 )

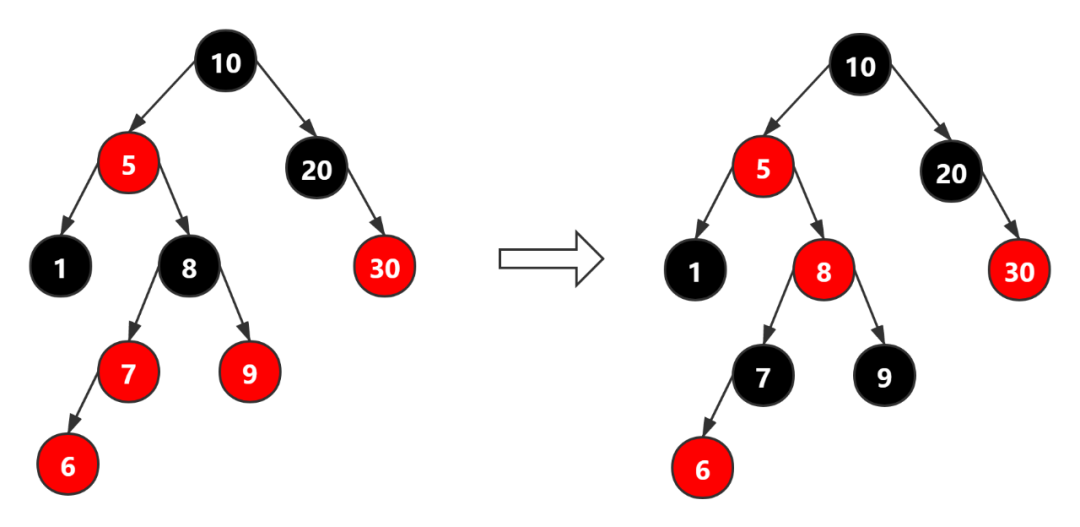
我们发现经过变化后，依旧不满足红黑树的原则，我们继续进行下一步操作

左旋转

当前父节点为红色，叔叔结点为黑色的时候，且当前的节点位于右子树，则以当前结点的父节点(5)进行左旋转

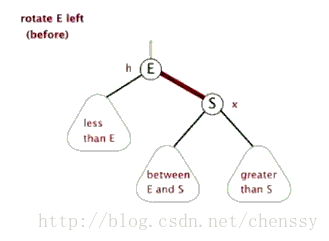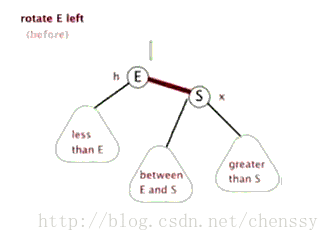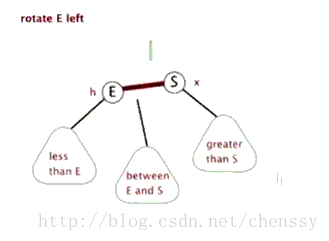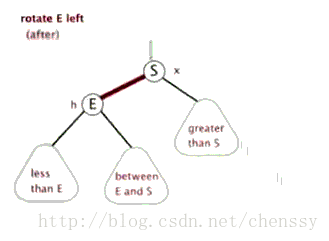
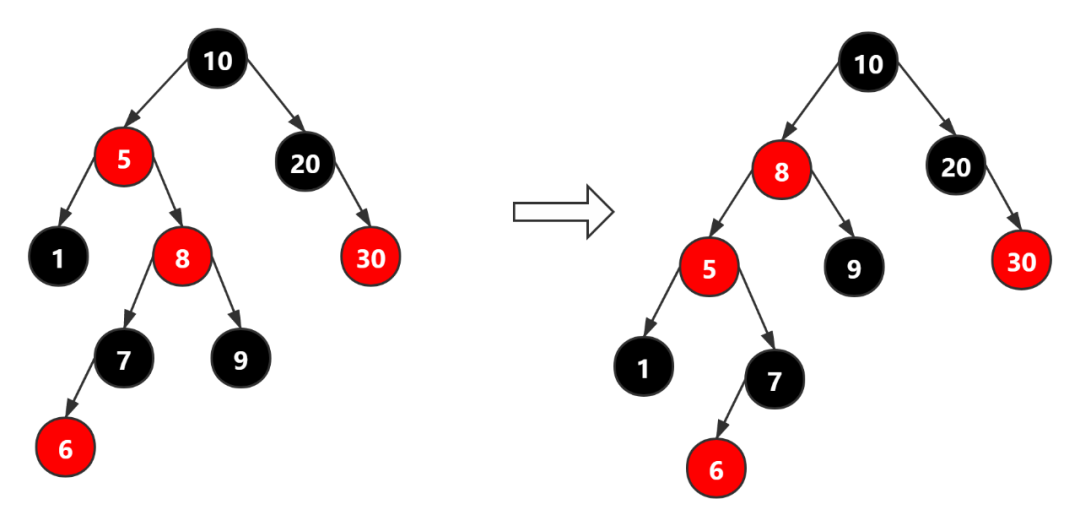
我们发现 经过变化 后， 依旧不满足红黑树的 原则 ，我们继续进行下一步操作

右旋转

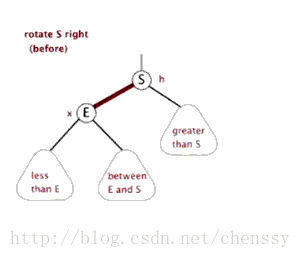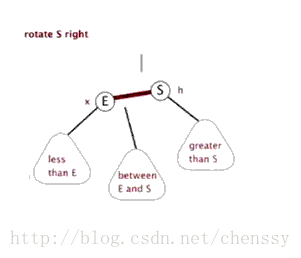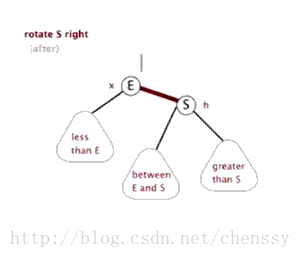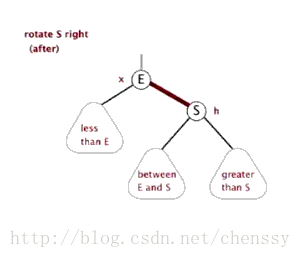
当前父节点是红色，叔叔结点是黑色的时候，且当前结点为左子树的时候

• 将父节点变为黑色

• 将祖父节点置为红色

• 以祖父节点进行右旋转

---

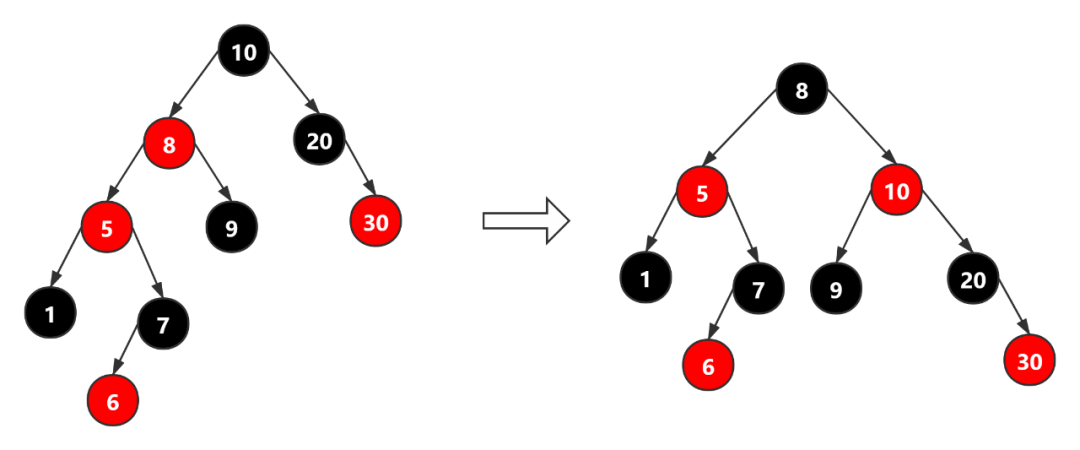
左左节点旋转（插入节点的父节点是左节点，插入节点也是左节点）

如下图所示的红黑树，我们插入节点是65。

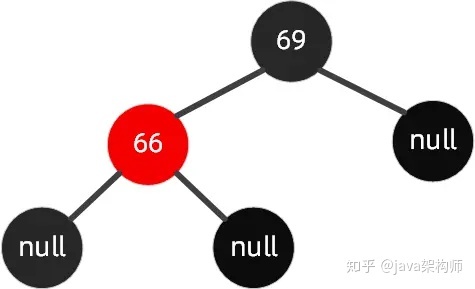
操作步骤如下可以围绕祖父节点 69 右旋，再结合变色，步骤如下所示：

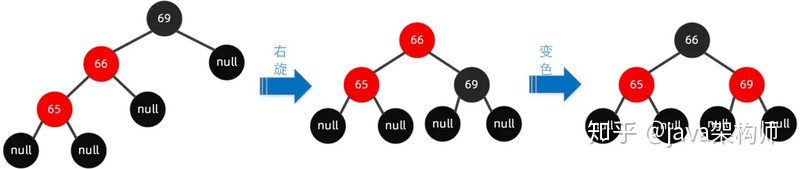
左右节点旋转（插入节点的父节点是左节点，插入节点是右节点）

还是上面这颗红黑树，我们再插入节点 67。

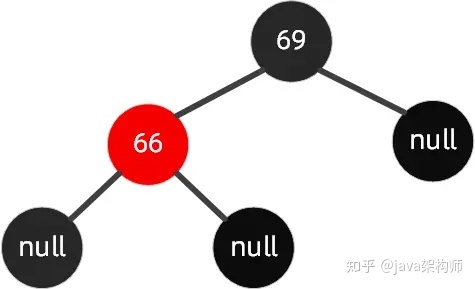
这种情况我们可以这样操作，先围绕父节点 66 左旋，然后再围绕祖父节点 69 右旋，最后再将 67 设置为黑色，把 69 设置为红色，如下图所示。

右左节点旋转（插入节点的父节点是右节点，插入节点左节点）

如下图这种情况，我们要插入节点68。

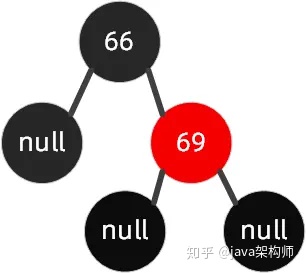
这种情况，我们可以先围绕父节点 69 右旋，接着再围绕祖父节点 66 左旋，最后把 68 节点设置为黑色，把 66 设置为红色，我们的具体操作步骤如下所示。

右右节点旋转（插入节点的父节点是右节点，插入节点也是右节点）

还是来上面的图来举例，我们在这颗红黑树上插入节点 70 。

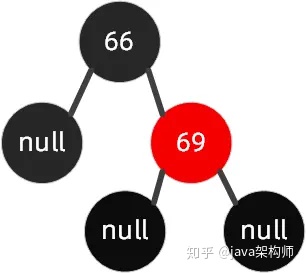
我们可以这样操作围绕祖父节点 66 左旋，再把旋转后的根节点 69 设置为黑色，把 66 这个节点设置为红色。具体可以参看下图：

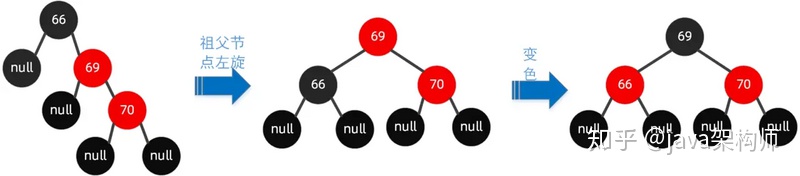
那么为什么当满足以上性质时，就能保证最长路径不超过最短路径的二倍了呢？

我们分析一下：

最短路径为全黑，最长路径就是红黑节点交替（因为红色节点不能连续），每条路径的黑色节点相同，则最长路径、刚好是最短路径的两倍。

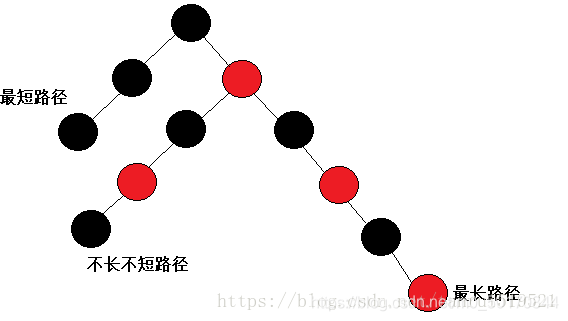
红黑树为什么删除效率高：

红黑树不追求"完全平衡"，即不像AVL那样要求节点的高度差 <= 1，它只要求部分达到平衡，但是提出了为节点增加颜色，红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，而AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。

就插入节点导致树失衡的情况，AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance，旋转的量级是O(1)

删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡，只需O(1)，所以说RB-Tree删除节点的rebalance的效率更高，开销更小！

AVL的结构相较于RB-Tree更为平衡，插入和删除引起失衡，如2所述，RB-Tree复衡效率更高；当然，由于AVL高度平衡，因此AVL的Search效率更高啦。

针对插入和删除节点导致失衡后的rebalance操作，红黑树能够提供一个比较"便宜"的解决方案，降低开销，是对search，insert ，以及delete效率的折衷，总体来说，RB-Tree的统计性能高于AVL.

故引入RB-Tree是功能、性能、空间开销的折中结果。

5.1 AVL更平衡，结构上更加直观，时间效能针对读取而言更高；维护稍慢，空间开销较大。

5.2 红黑树，读取略逊于AVL，维护强于AVL，空间开销与AVL类似，内容极多时略优于AVL，维护优于AVL。

总结：

实际应用中，若搜索的次数远远大于插入和删除，那么选择AVL，如果搜索，插入删除次数几乎差不多，应该选择RB。