【2022 408】红黑树知识点总结

• 红黑树

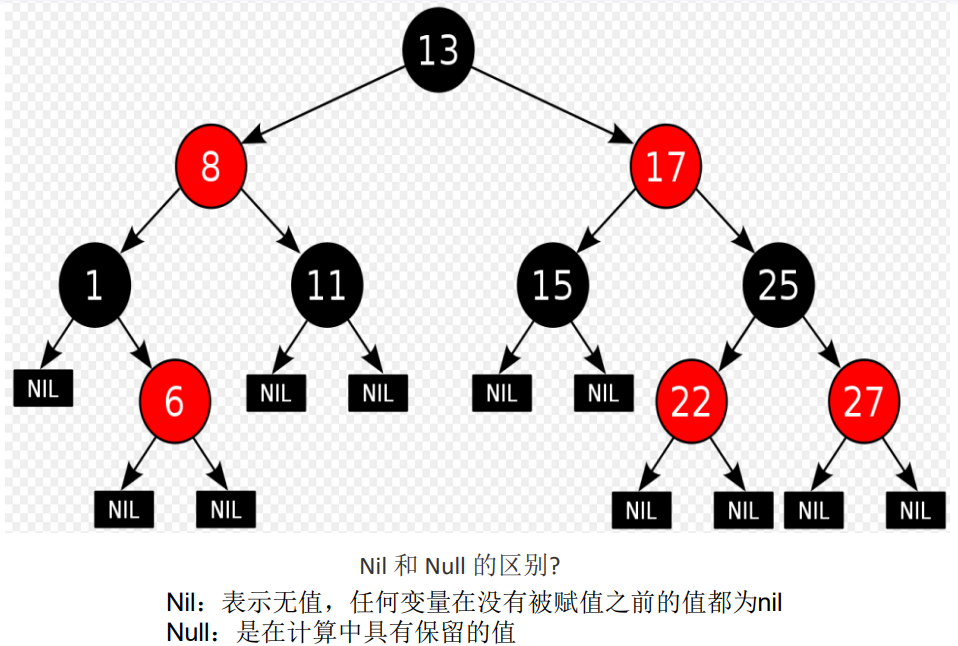
  • 概述

    

    

  • 性质

    • 每个节点的颜色只能是红色/黑色
    • 根节点是黑色
    • 每个叶子节点都带有两个空的黑色节点(哨兵)，若一个节点n只有一个左孩子，那么n的右孩子是一个黑哨兵；如果结点n只有一个右孩子，那么n的左孩子是一个黑哨兵。
    • 如果一个结点是红的，则它的两个儿子都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
    • 对于每个结点来说，从该结点到其子孙叶结点的所有路径上包含相同数目的黑结点。

  • 操作特性

    • 每一个红黑树也是一个二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。
    • 在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。
    • 恢复红黑树的性质需要少量(O(log n))的颜色变更和不超过三次树旋转(对于插入操作是两次)。
    • 虽然插入和删除很复杂，但操作时间仍可以保持为 O(log n) 次。

  • 自平衡

    • 左旋

      

      
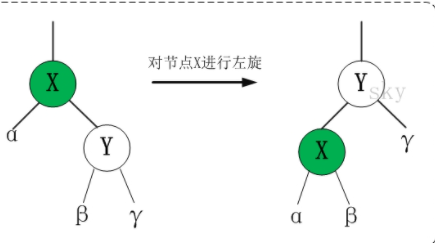
      以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。
      • 算法实现

        

    • 右旋

      

      
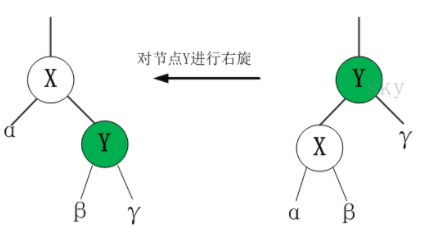
      以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。
      • 算法实现

        

    • 变色
      变色：结点的颜色由红变黑或由黑变红。

  • 查找算法

    

  • 插入算法

    

    

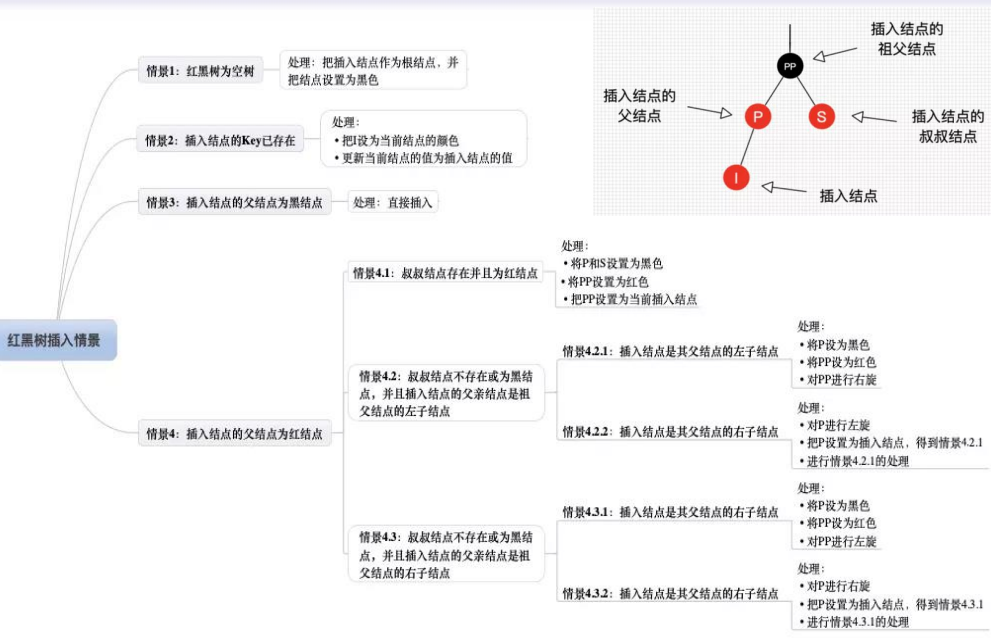
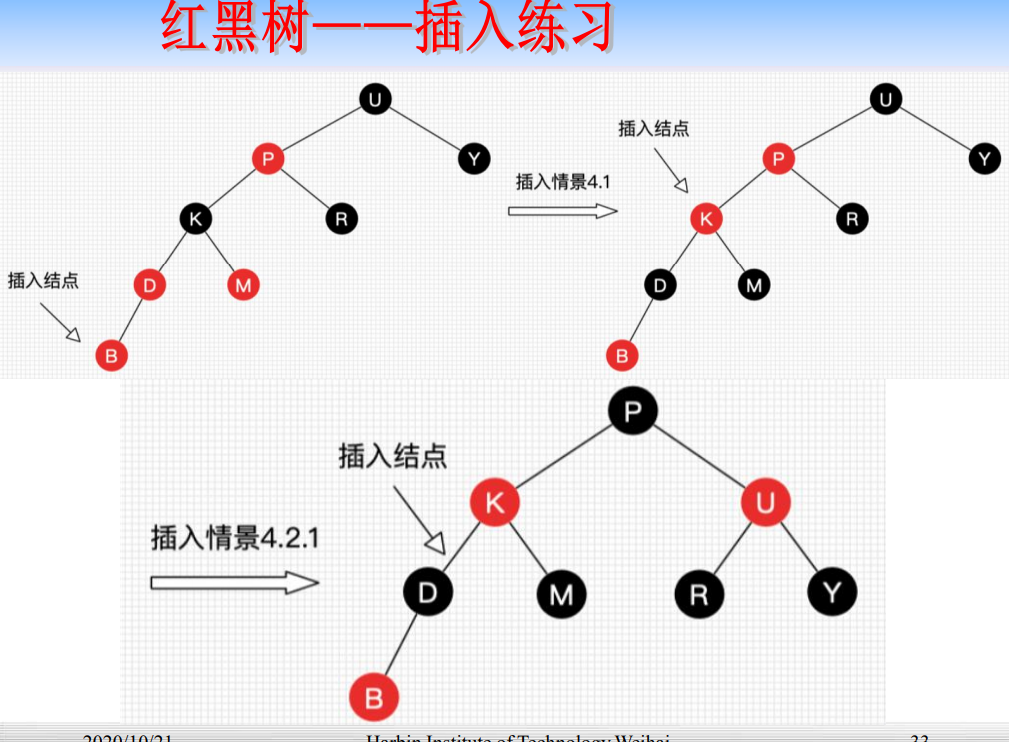
    • 首先以二叉查找树的方法增加节点并标记为红色
    • 进行二叉查找树中插入节点的算法

      

      

    • 新插入节点设置为红色后，可能会导致出现两个连续红色节点的冲突，那么可以通过颜色调换和树旋转调整（修正操作）

      

      • 情形1：没有父节点，新节点N位于树的根上——将新节点重绘为黑色
        红黑树为空树 满足性质2
      • 情形2：新节点的父节点P是黑色，所以性质4没有失效（新节点是红色的）。
        树有效，满足性质4 5
      • 新节点的父节点为红色

        

        • 情形3：N是新节点，如果父节点P和叔父节点U二者都是红色。

          

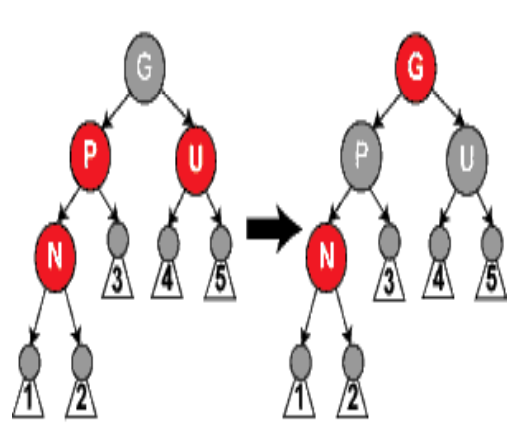
          • 将父节点和叔父节点重绘为黑色，祖父节点重绘为红色
            新节点N有了一个黑色的父节点P。在这些路径上的黑节点数目没有改变。
          • 但是，红色的祖父节点G的父节点也有可能是红色的，这就违反了性质4。为此在祖父节点G上递归地进行情形1的整个过程。把祖父节点G当做新节点进行检查
        • 情形4：N是新节点，父节点P为红色而叔父节点U是黑色或者缺少，N为P的左孩子，P又是G的左孩子

          

          
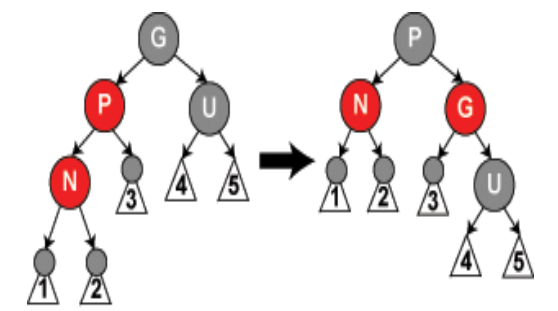
          若P和U位置对调，则在下面的第二步进行左旋转
          • P设为黑色，G设为红色
          • 进行针对祖父节点G的右旋转
            之前的父节点P现在是新节点N和以前的祖父节点G的父节点，满足性质4 5
        • 情形5：N是新节点，父节点P是红色而叔父节点U是黑色或缺少，N为P的右孩子，P又是G的左孩子

          

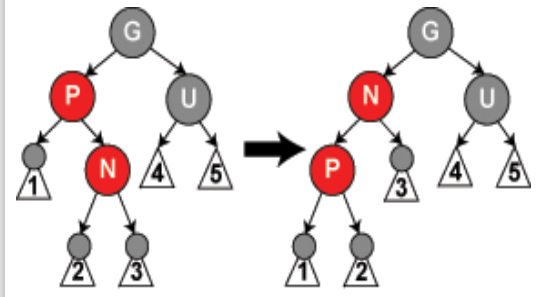
          • 进行针对P的左旋调换N和P的角色
          • 把P设置为插入节点，进行情形4的处理

  • 删除算法

    

    

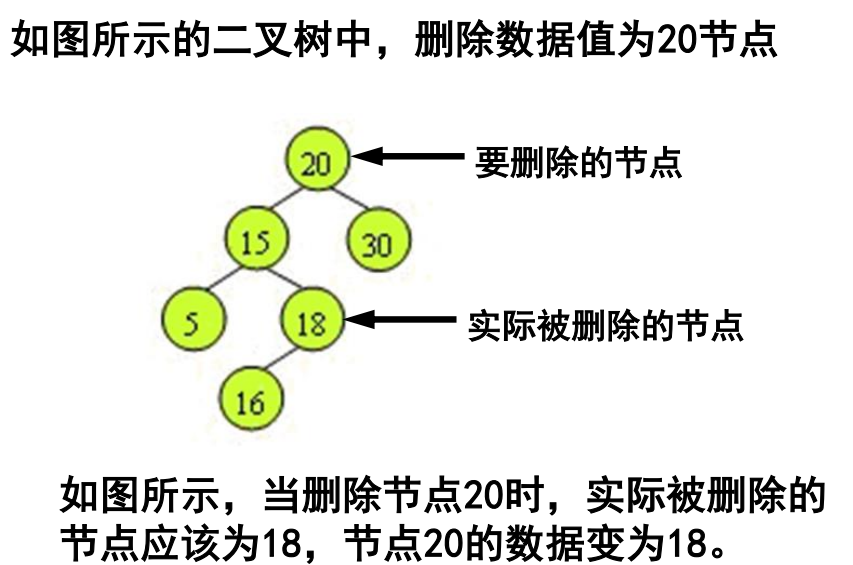
    • 首先，将红黑树当做一棵二叉查找树，将该节点从二叉查找树中删除

      

    • 然后，通过“旋转和重新着色”等一系列来修正该树，使之重新成为一棵红黑树。

      

      
      分三种情况
      • 普通二叉树操作
        • 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了。
        • 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
        • 被删除节点有两个儿子。那么，把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。
      • 红黑树操作

        

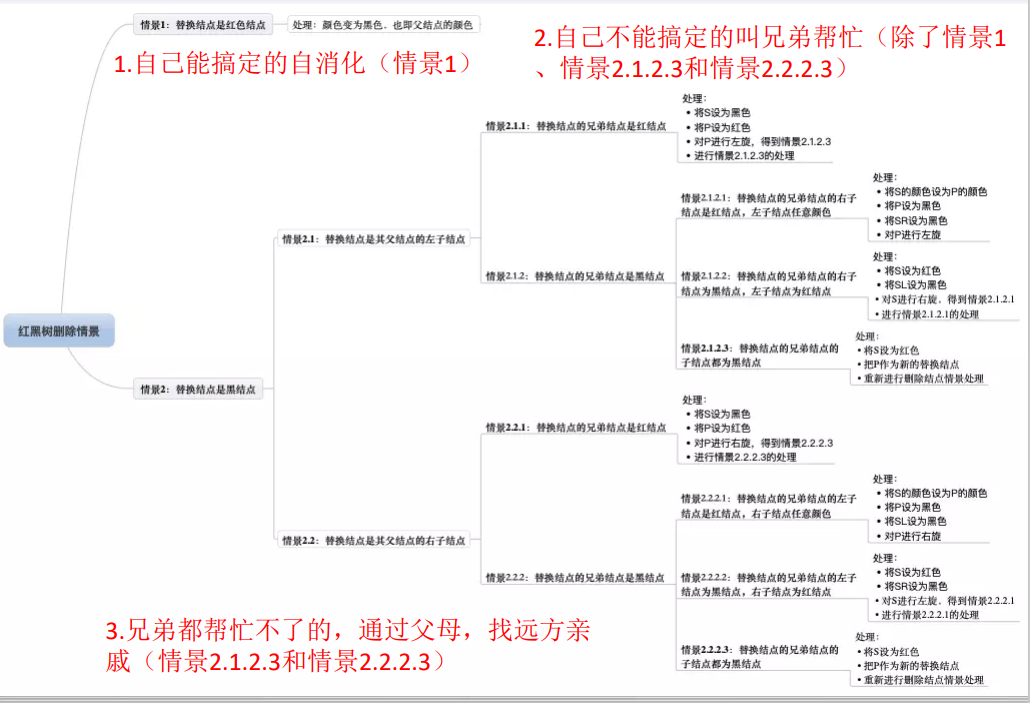
        • 情形1：删除节点无子节点，则删除节点可能为红色/黑色
          • 红色直接删除

            

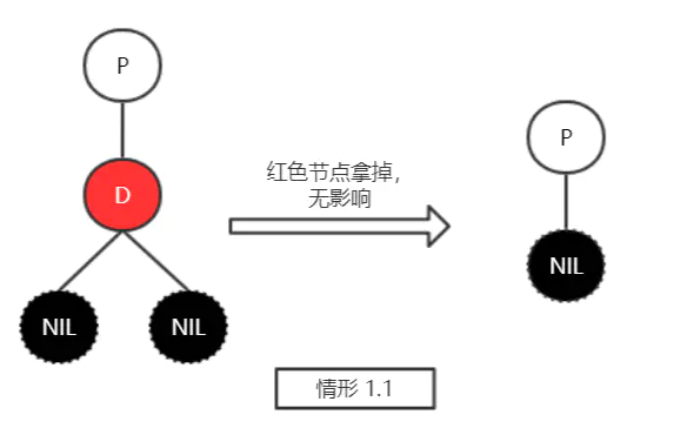
          • 黑色，删除平衡操作

            

            
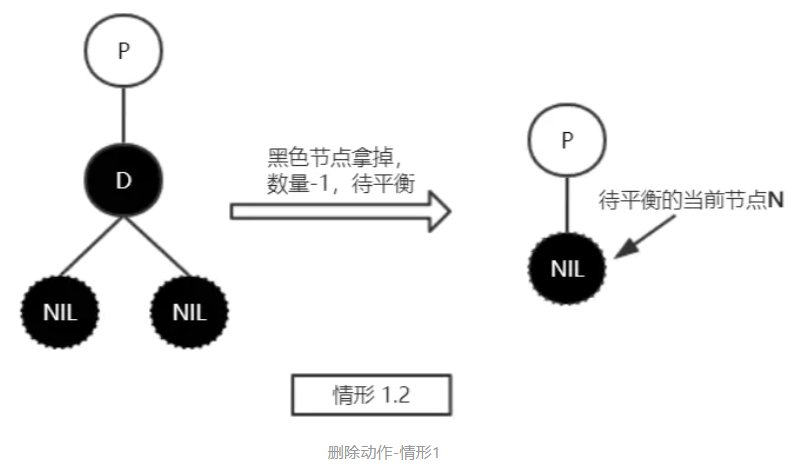
            对于红黑树来说可能失衡，因为nil是黑色，删除该节点相当于该分支上少了一个黑色节点
        • ➢ 我们只需要讨论删除只有一个儿子的节点
          • 情形2：只有一个子节点时，删除节点只能是黑色，其子节点为红色，否则无法满足红黑树的性质了。 此时用删除节点的子节点接到父节点，且将子节点颜色涂黑，保证黑色数量

            

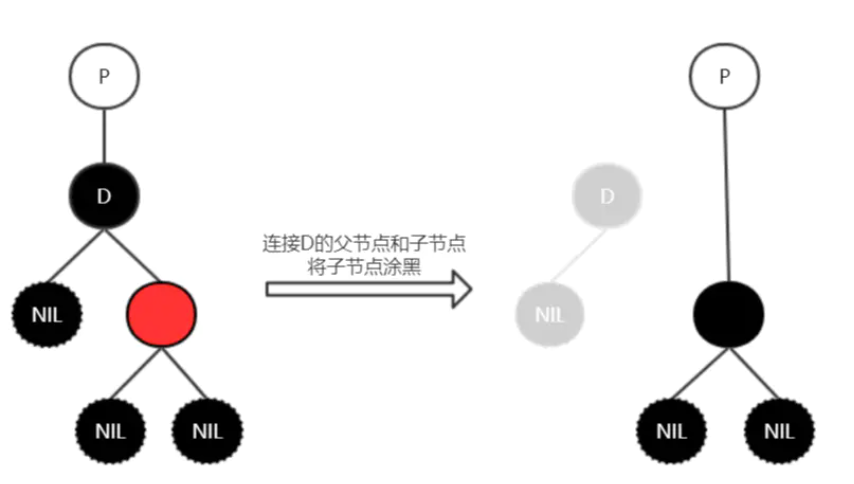
          • ➢ 如果它两个儿子都为空，我们任意将其中一个看作它的儿子。
          • ➢ 如果需要删除的节点有两个儿子，那么问题可以被转化成另一个删除只有一个儿子的节点的问题
        • ➢ 难点在于要删除的节点和它的儿子二者都是黑色的时候——平衡操作

          

          
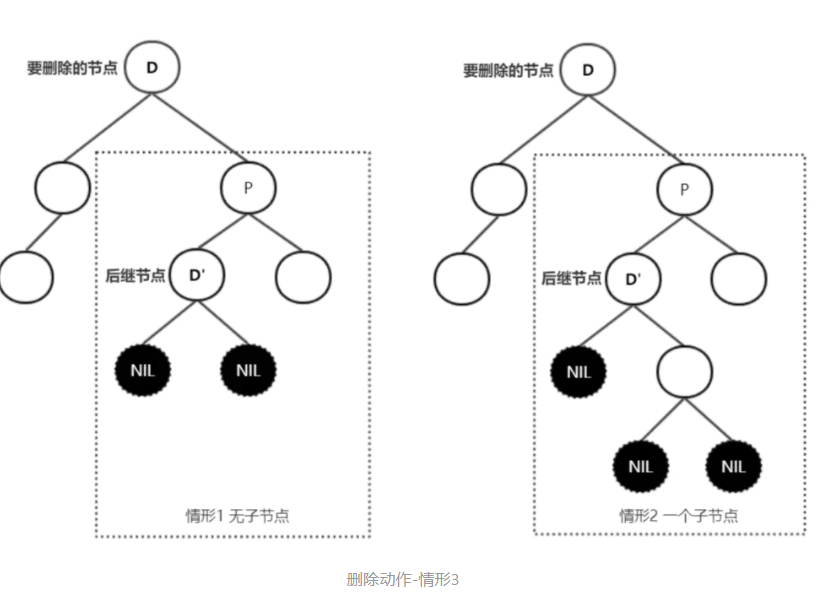
          如果儿子N和它原始的父亲是黑色，则删除父亲导致通过N的路径都比不通过它的路径少了一个黑色节点。 这违反了性质5，需要重新平衡。
          • 替代节点

            

            

            
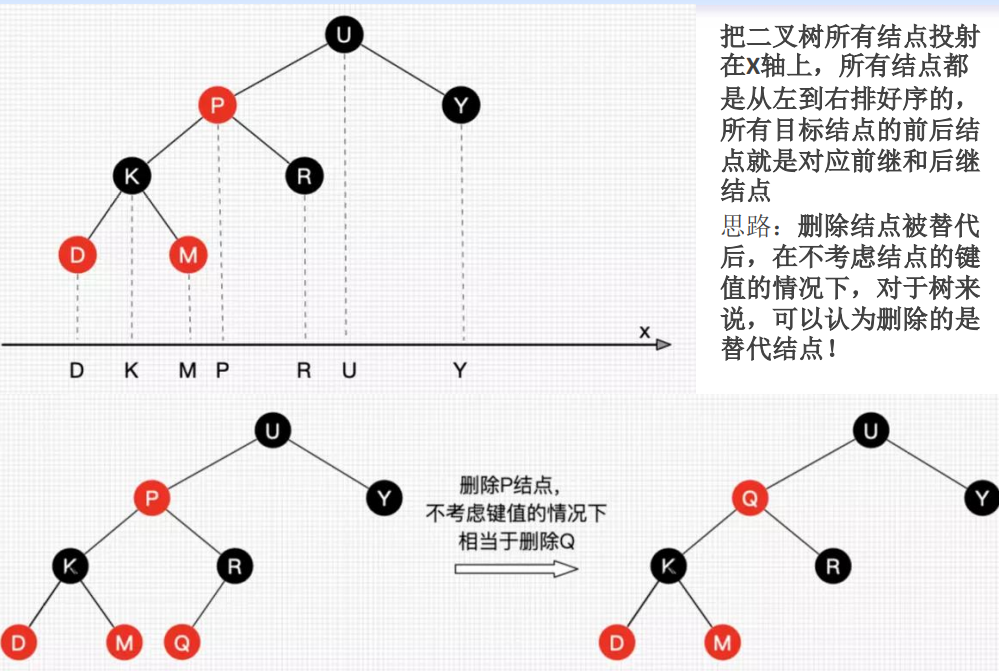
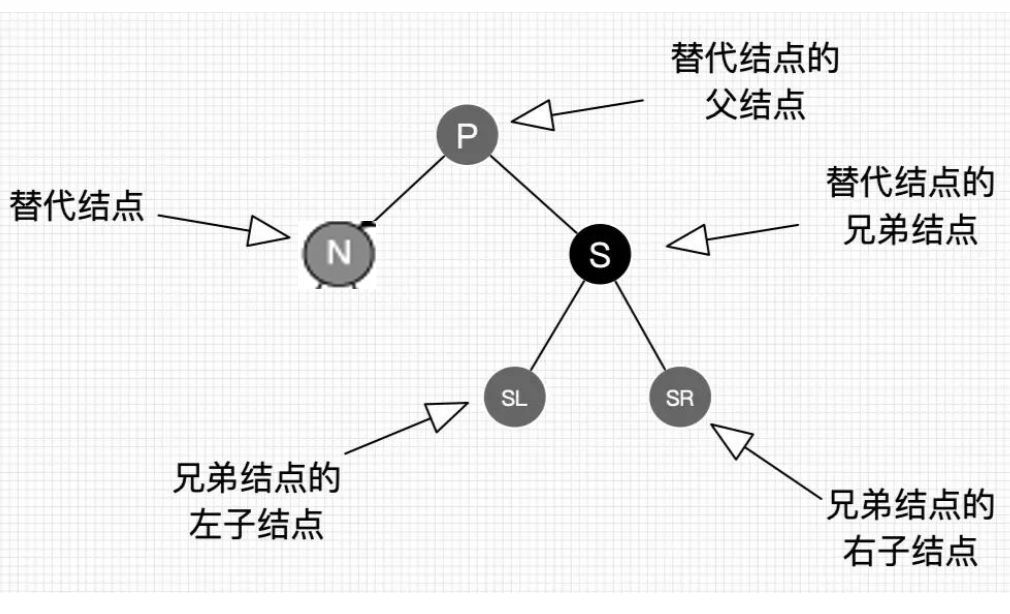
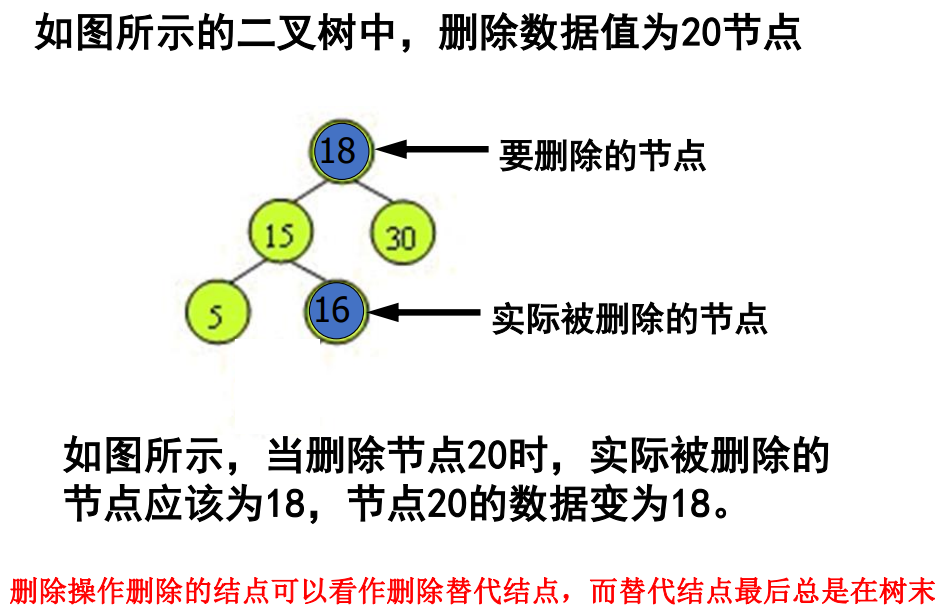
            投射后，找被删除节点最近节点做替代，一般找大于删除节点的最小节点，删除操作删除的结点可以看作删除替代结点，而替代结点最后总是在树末
          • 情形1：替换节点为黑色，删除后儿子N为新的根
            N即为替代节点，删除了一个黑色，新根是黑色，性质都保持
          • 情形2：替换节点为黑色，S为红色

            

            
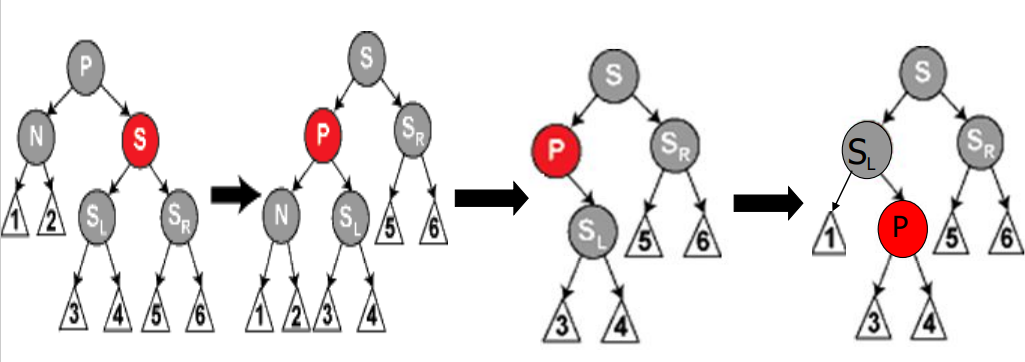
            先变换后删除
          • 情形3：删除后新节点N的父亲P，兄弟S和S的儿子都是黑色

            

            
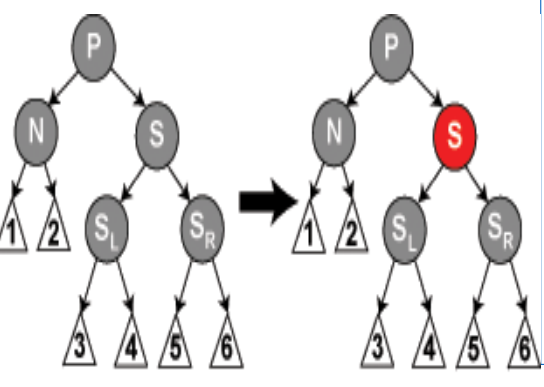
            重绘S为红色
            简单的重绘S为红色。结果是通过S的所有路径，都少了一个黑色节点。因为删除N的初始的父亲使通过N的所有路径少了一个黑色节点，这使事情都平衡了起来。但是，通过P的所有路径现在比不通过P的路径少了一个黑色节点，所以仍然违反性质5。要修正这个问题，我们要从情形1开始，在P上做重新平衡处理
          • 情形4：替代节点N、S和S的儿子都是黑色，但是N的父亲是红色

            

            
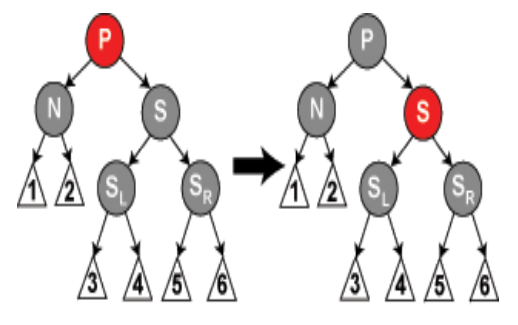
            在这种情形下，交换N的兄弟和父亲的颜色。这不影响不通过N的路径的黑色节点的数目，但是它在通过N的路径上对黑色节点数目增加了一，添补了在这些路径上删除的黑色节点。
          • 情形5：删除后新节点N的S是黑色，S的左儿子是红色，S的右儿子是黑色

            

            
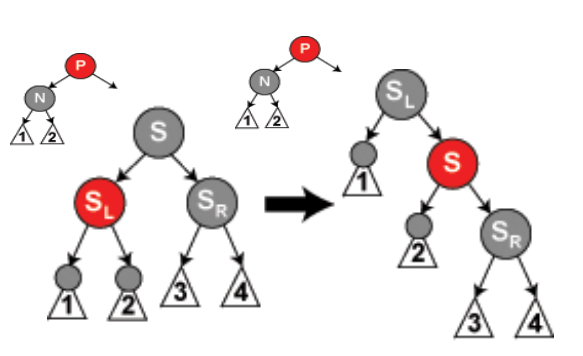
            在S上做右旋转，这样S的左儿子成为S的父亲和N的新兄弟。接着交换S和它的新父亲的颜色。所有路径仍有同样数目的黑色节点，但是现在N有了一个右儿子是红色的黑色兄弟，所以我们进入了情形6。N和它的父亲都不受这个变换的影响。
          • 情形6：调整后N节点的S是黑色，S的右儿子是红色，而N是它父亲的左儿子。

            

            
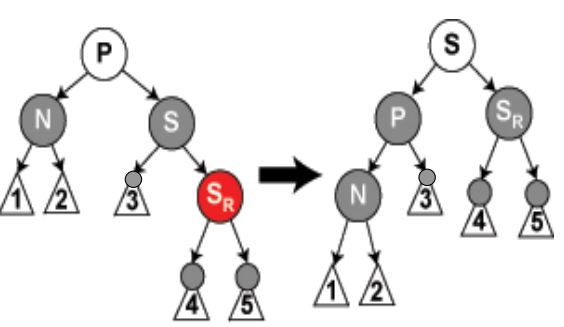
            在这种情形下我们在N的父亲上做左旋转，这样S成为N的父亲（P）和S的右儿子的父亲。接着交换N的父亲和S的颜色，并使S的右儿子为黑色。子树在它的根上的仍是同样的颜色，所以性质3没有被违反。

  • 红黑树应用

    • 并行数据库
    • 内存数据库
    • 设计可近似匹配的索引数据结构