树 相关知识

二叉树 树的任意节点最多两棵子树。

完美二叉树 perfect 除了叶子结点，每个节点都有两个孩子，每层也是完全填充的。

完整二叉树 complete 除了最后一层之外的其他层都被完全填充，并且所有节点都保持向左对齐。

完满二叉树 full 除了叶子结点外每个节点都有两个孩子。

完全二叉树中，若一个结点没有左孩子，则它必是树叶

答案：T

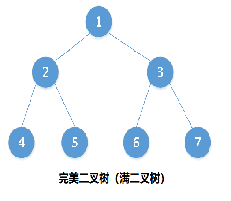
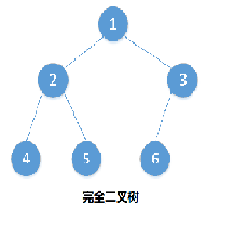
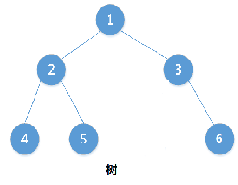
分析：

首先明确完全二叉树的定义：如果编号i（1≤i≤n）的结点与满二叉树（完美二叉树）中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

图1为完美二叉树（满叉树），图2为完全二叉树，两树相同序号的结点在树的位置上相同，而图三6号位置与图一位置不同，则它不是完全二叉树。

所以完全二叉树如果没有左结点，则一定没有右结点，即没有左孩子，它就一定是树叶。

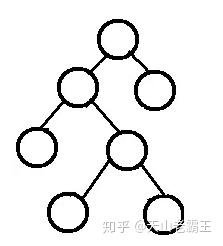
完满二叉树

二、二叉查找树（二叉搜索树、二叉排序树、BST）[这几个都是别名]

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

二叉搜索树的性能分析

1、插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。

2、但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：O(log n)

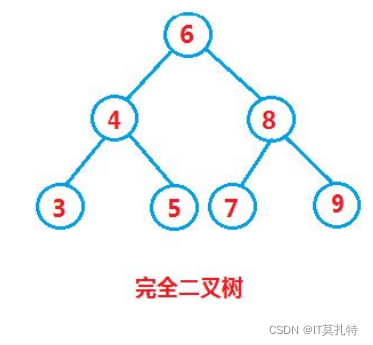
最坏情况下，二叉搜索树为右单支，其平均比较次数为：O(n / 2)（1~n）

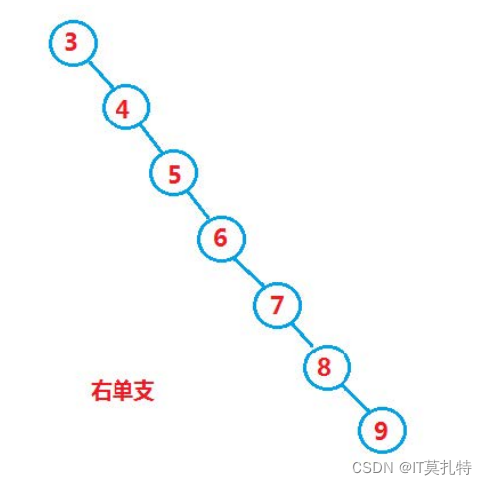
三、平衡二叉树

它具有以下两个性质：

• 可以是空树。

• 假如不是空树，任何⼀个结点的左子树与右子树都是平衡⼆叉树，并且高度之差的绝对值不超过 1。

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），它的性质很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

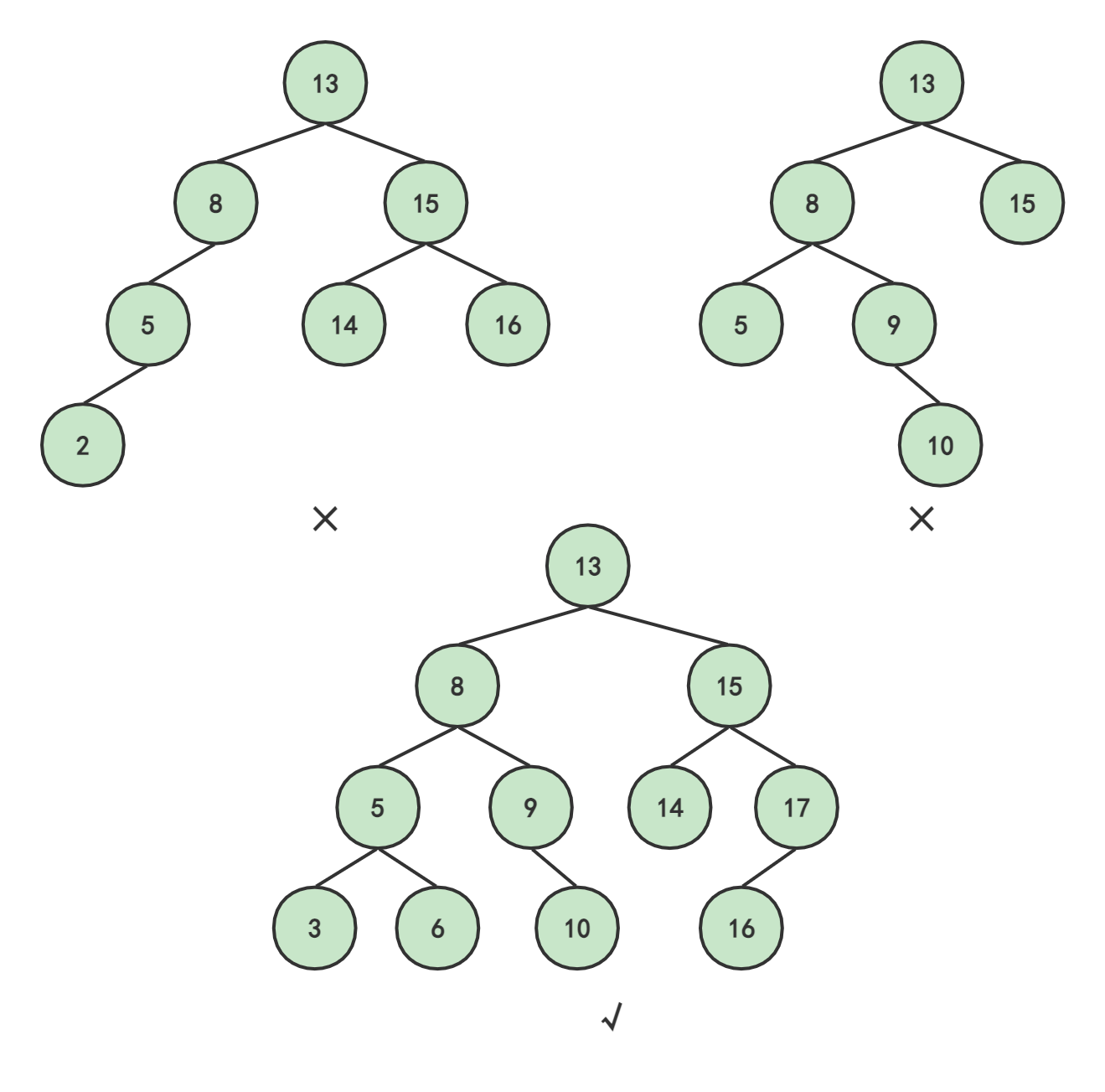
第一张图：8的左子树高度为2，右子树高度为0，失衡
第二张图：13的左子树高度为3，右子树高度为1，失衡
第三张图：每一个结点的左右子树高度差绝对值不超过1，平衡
于是，图1、图2不是平衡二叉树，图3是平衡二叉树。
另外，对于图1和图2：分别只有结点13、8失衡，其他结点都平衡。

3.插入

平衡因子

某结点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor）。平衡⼆叉树中不存在平衡因子大于于 1 的节点。

在⼀棵平衡⼆叉树中，节点的平衡因子只能取0、1、-1
0 ：左右子树等高
1：左子树比较高
-1 ：右子树比较高

3.2旋转

我们给出的方法是旋转这个树。怎么旋转呢？先别急，我们先介绍一个概念，以帮助我们更好的解释旋转。

最小失衡子树：在新插入的结点向上找，以第一个平衡因子绝对值大于1的结点为根的子树称为最小失衡子树。例如：上树中以父节点13的根的树为最小失衡子树。

显然，这时候13也是整课树的根结点，但往往更多的时候，失衡结点也不一定是全树的根结点，很可能只是某一部分子树失衡了，所以我们也只需要调整失衡的子树，其他部分不用调整。那么是怎么调整的呢？

平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的，旋转分为左旋和右旋，其目的，就是减少树的高度（哪边高，就把那边向上旋转）。

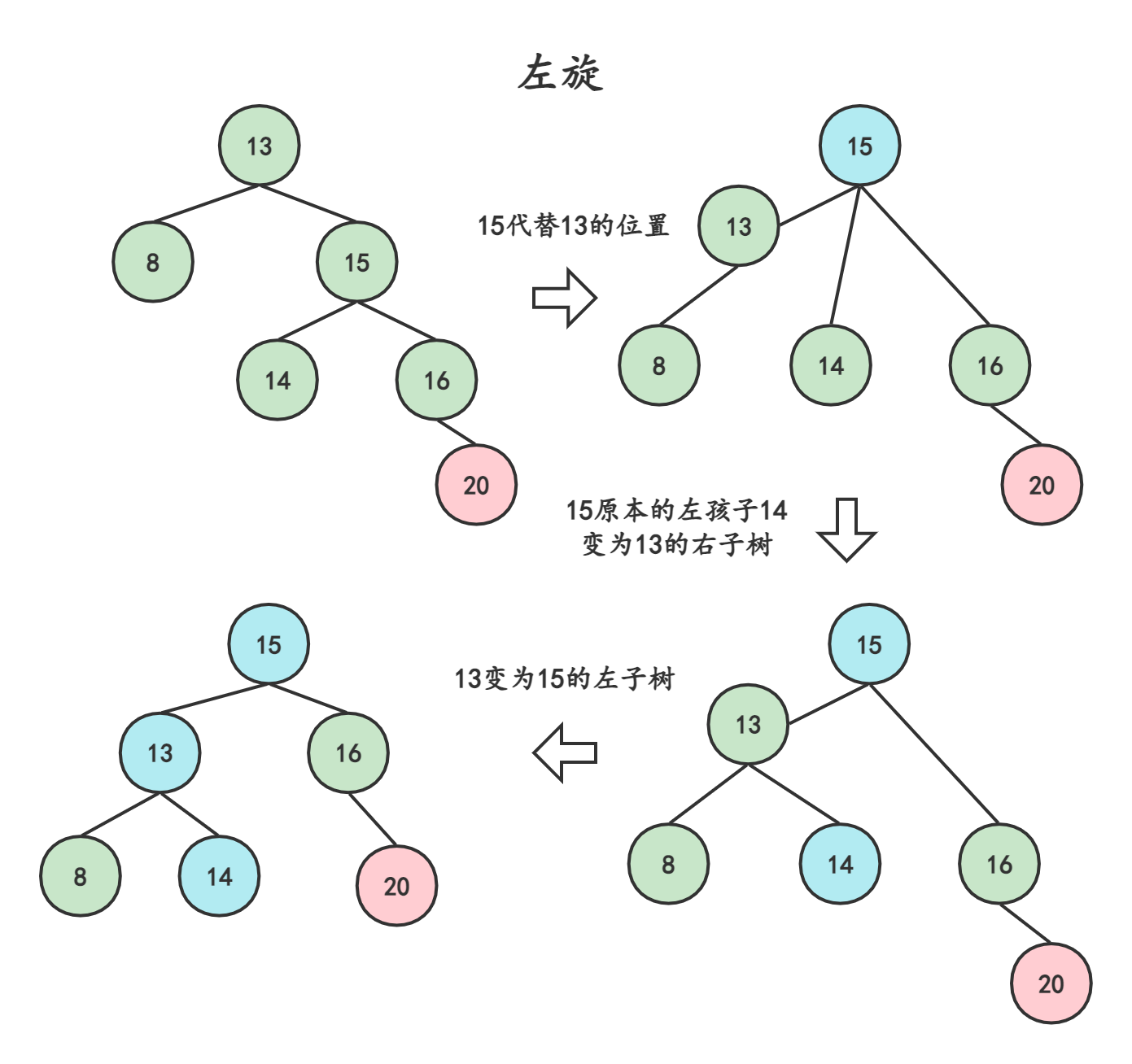
3.2.1左旋—右孩子右子树

结点的右孩子替代此结点的位置
右孩子的左子树变成结点的右孩子
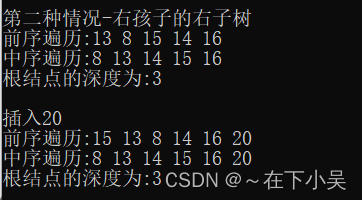
结点本身变成右孩子的左子树

以下图为例，在插入结点20后。结点13发生了失衡，需要对13为父节点的子树进行旋转，由于插入的位置是在13右孩子的右子树上，所以我们通过左旋的方式来实现。

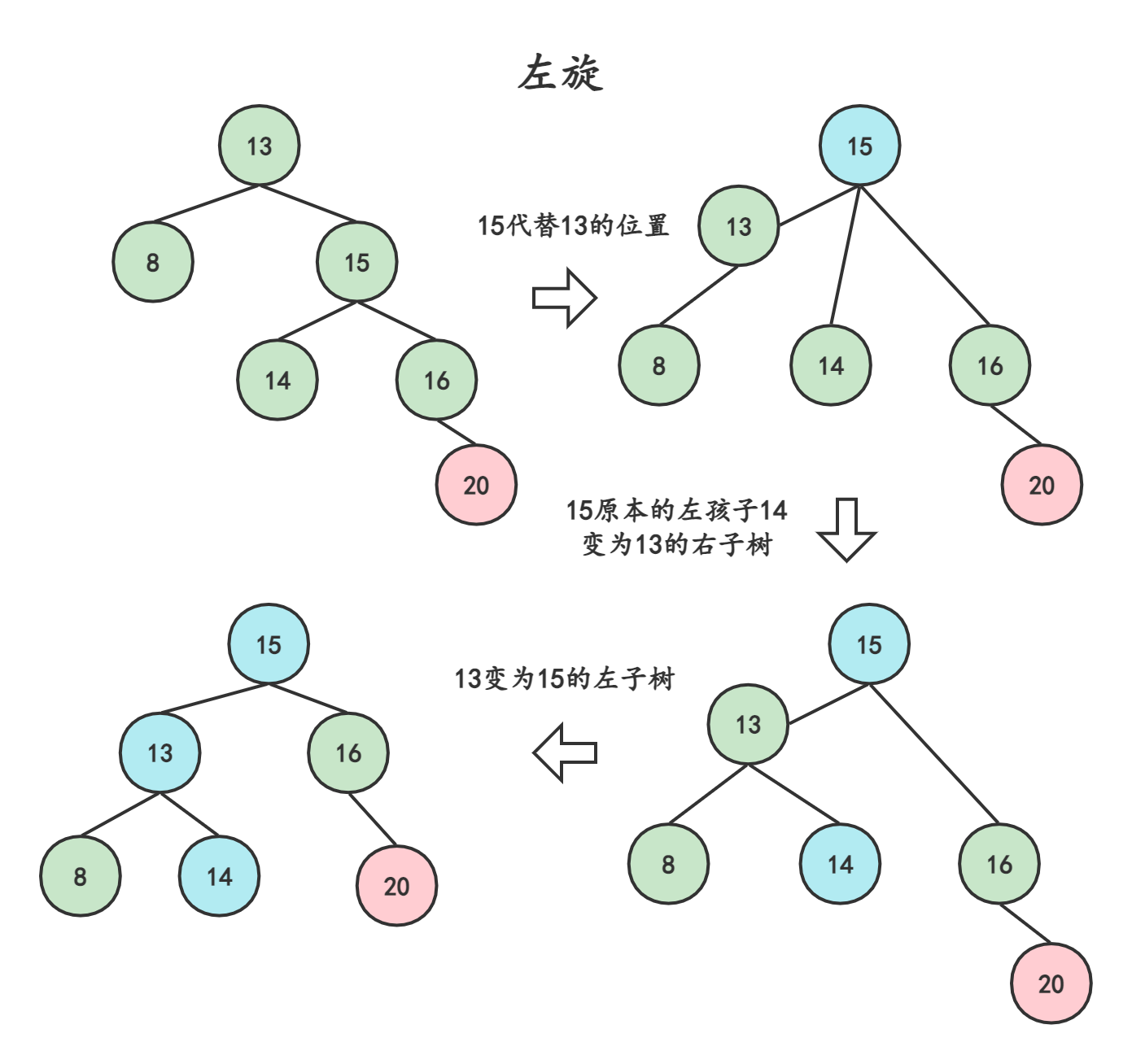
通过上述操作，我们把15向上旋转了，让原本的父节点13作为了15的左孩子，此时就变成了三叉树，需要将15原本的左子树接到13的右孩子处（这样，15也是二叉树，14的位置也是对的）

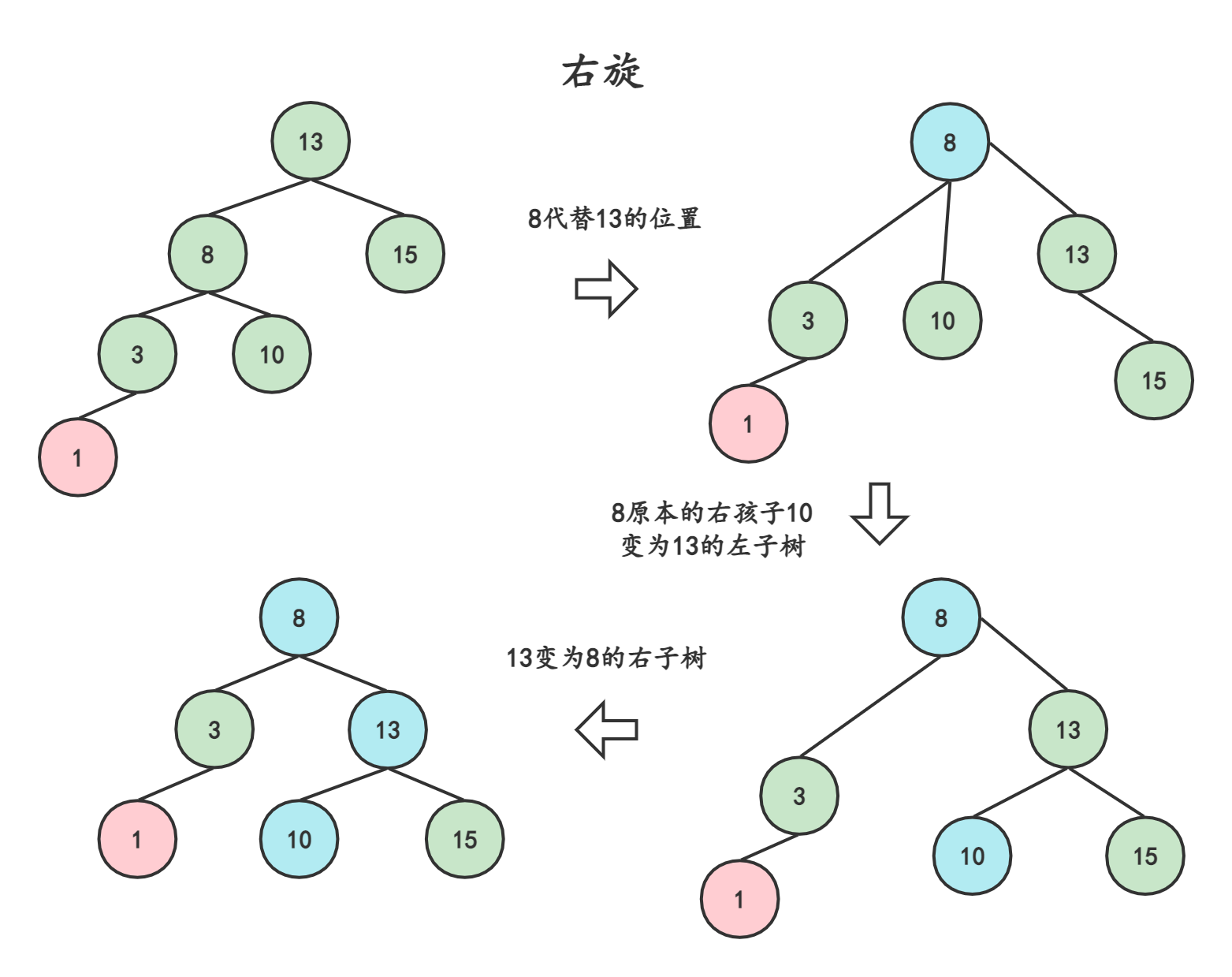
3.2.2右旋-左孩子左子树

那如果是在左孩子的左子树插入结点导致失衡的呢？就采用与右旋相对应的左旋（右与左互换）。

结点的左孩子替代此结点的位置
左孩子的右子树变成结点的左孩子
结点本身变成左孩子的右子树

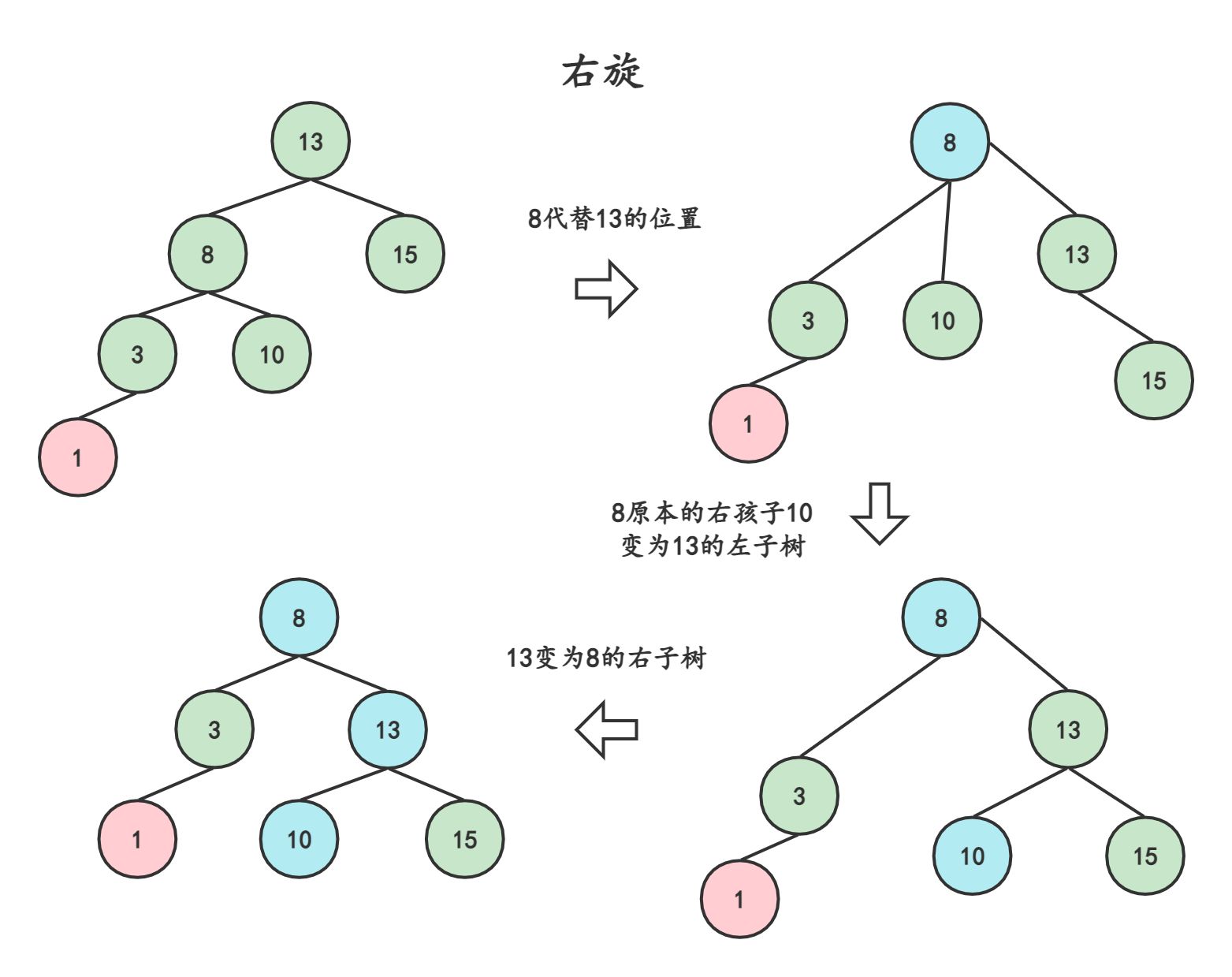
通过上述操作，我们把8向上旋转了，让原本的父节点13作为了8的右孩子，此时就变成了三叉树，需要将8原本的右子树接到13的右孩子处（这样，8也是二叉树，10的位置也是对的）

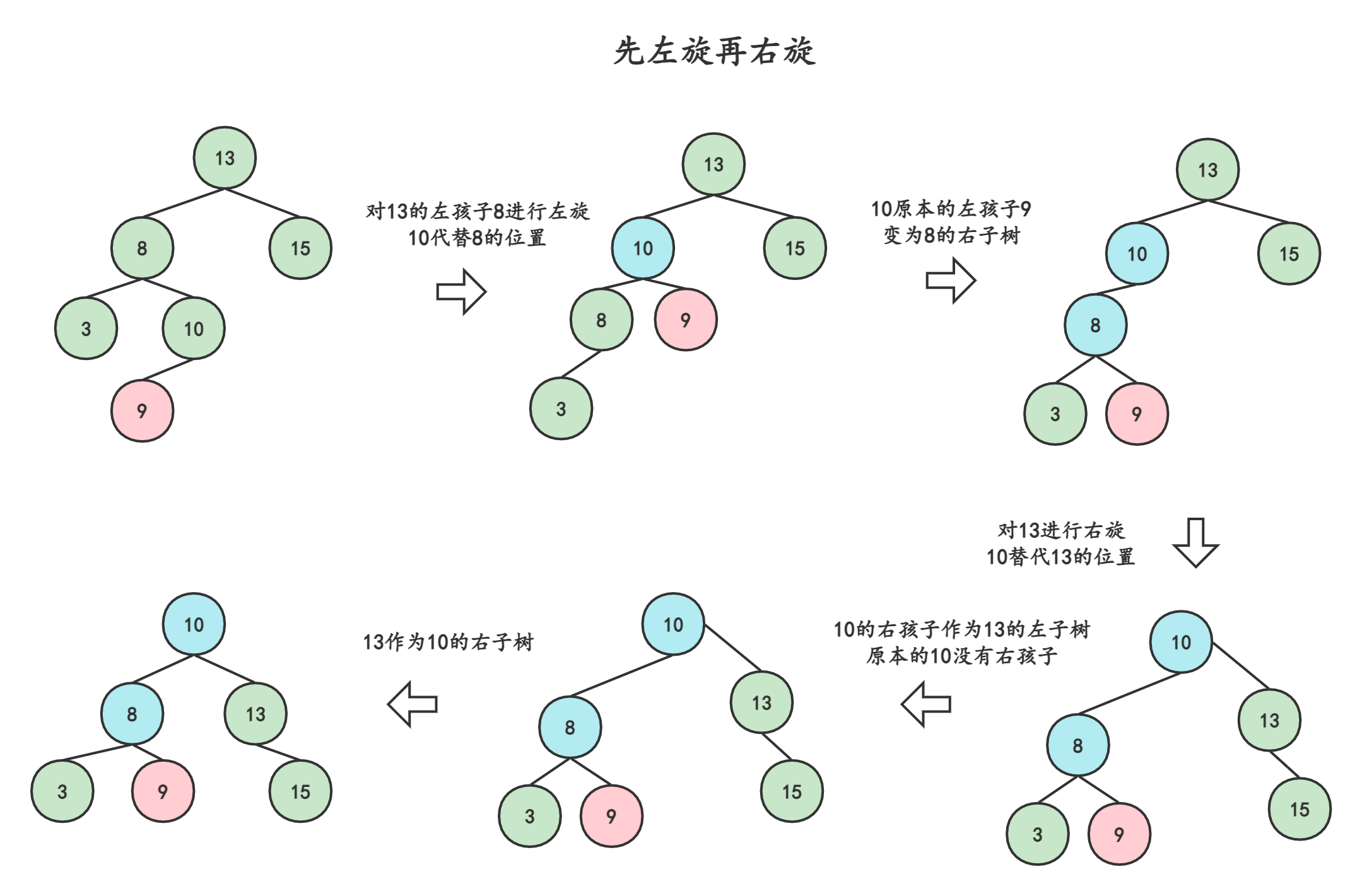
3.2.3先左旋再右旋-左孩子右子树

这里我们解决了两种插入方式了，但还有两种，如果是在左孩子的右子树或者右孩子的左子树插入导致失衡呢？我们接着看。

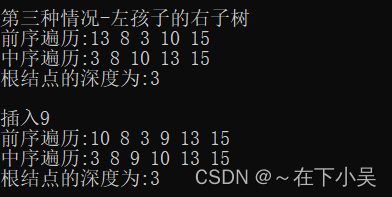
左孩子的右子树，即在10的位置插入了元素9，导致13失衡，而插入结点9在13的左孩子8的右子树上。此时，我们先对13的左孩子8左旋，再对13右旋。其中，左右旋操作即3.2.1与3.2.2介绍的操作。

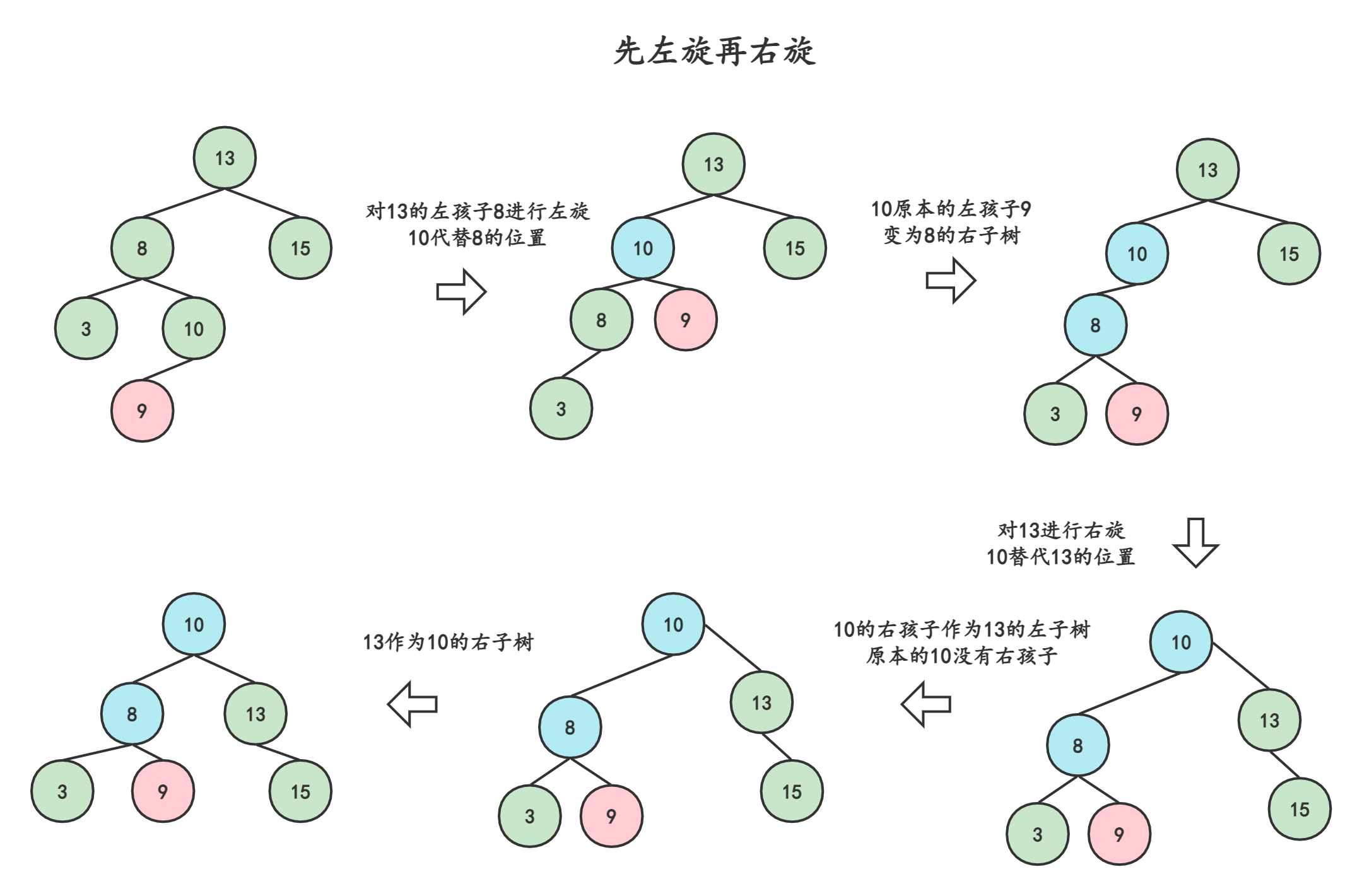
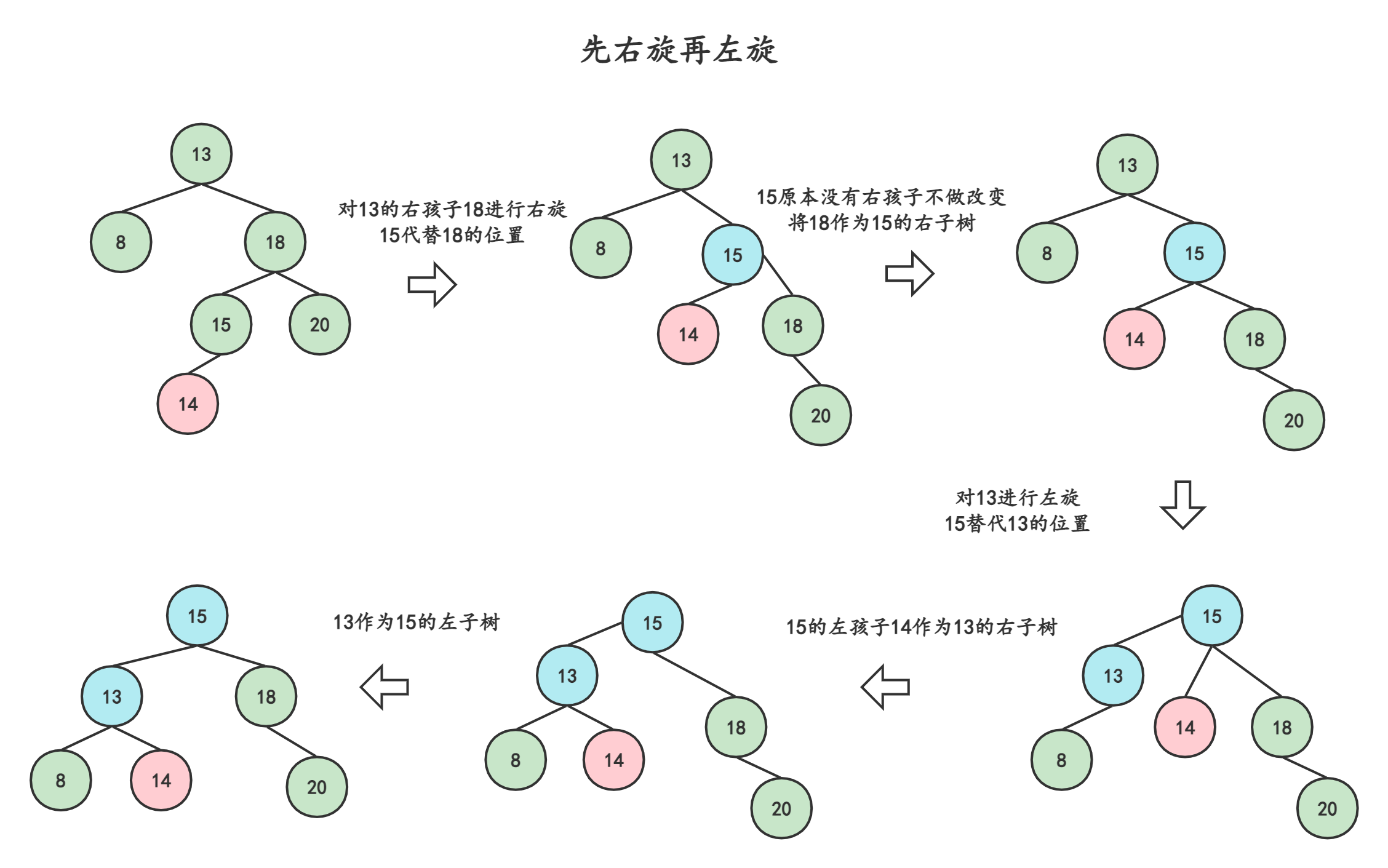
3.2.4先右旋再左旋-右孩子左子树

那如果是右孩子的左子树插入呢？我们依然采用相对应3.2.3的方式（左右互换）。

插入元素14,14按理应放在15后面，于是导致了13失衡。先对失衡结点13右孩子18右旋，再对13左旋。

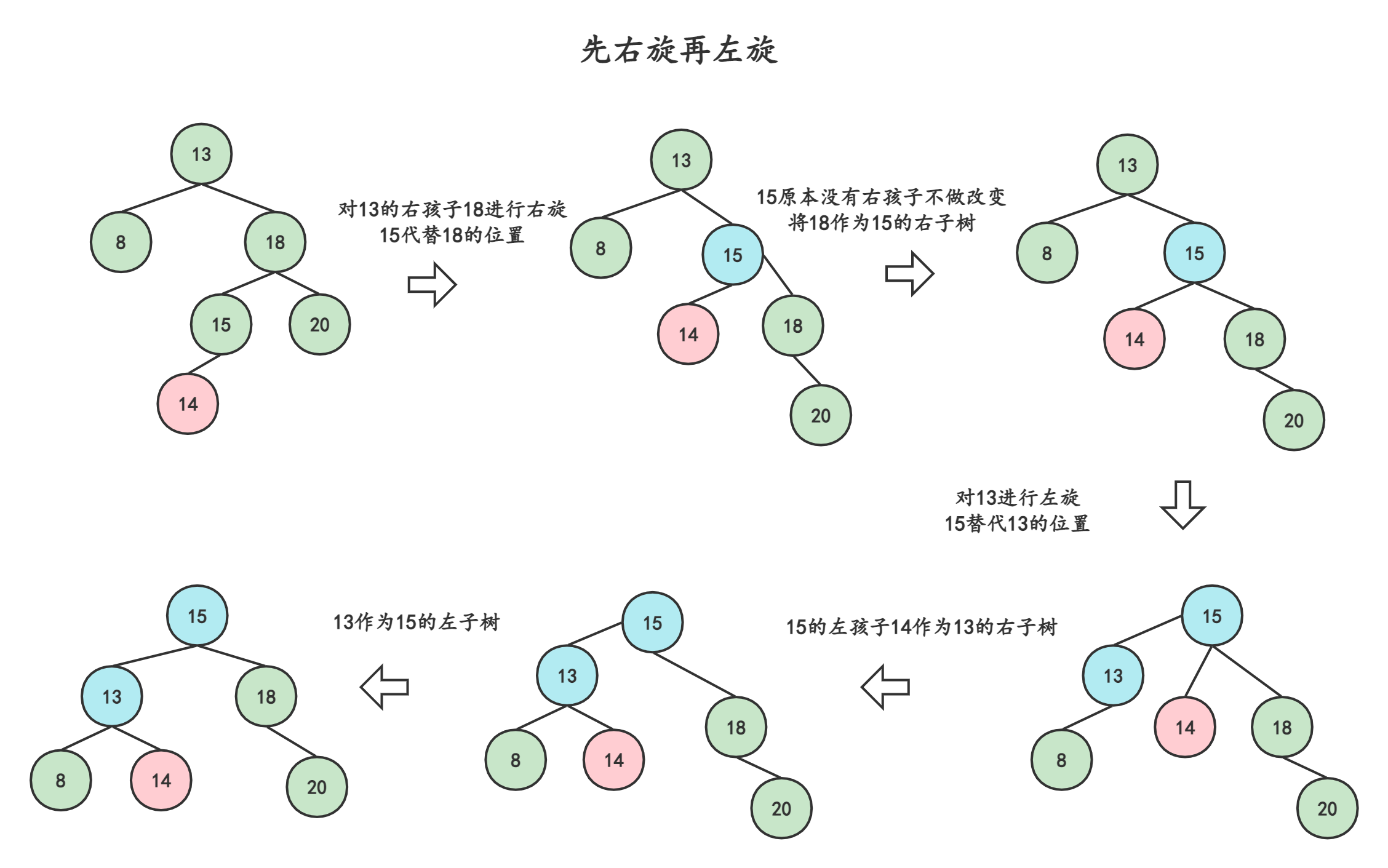
3.3总结

根据以上四种插入方式，旋转方式总结如下：

插入方式	描述	旋转方式
LL	在结点A的左孩子的左子树插入导致A失衡	右旋
RR	在结点A的右孩子的右子树插入导致A失衡	左旋
LR	在结点A的左孩子的右子树插入导致A失衡	先左旋再右旋
RL	在结点A的右孩子的左子树插入导致A失衡	先右旋再左旋

注意：“先左旋”旋转的是失衡结点的左子树，“再右旋”旋转的是失衡结点。

4.删除

在介绍完插入操作后，我们自然地应该来看看删除操作。删除的思想也同二叉排序树，但需要注意的是删除结点可能会导致树失衡，而且删除此结点，可能导致其他很多结点都失衡。也就是说：插入只需要修正第一个非平衡结点（1个），即可平衡；而删除需要修正所有的非平衡结点。

所以，它比插入操作更复杂，但没关系，我们继续分类讨论：

删除结点的类型：
删除叶子结点
删除结点只有左子树
删除结点只有右子树
删除结点有左、右子树

4.1删除叶子结点

将该节点直接从树中删除
其父结点的子树高度的变化将导致父节点平衡因子的变化，通过向上检索并推算其父节点是否失衡；
如果其父节点未失衡，则继续向上检索推算其父节点的父节点是否失衡…如此反复步骤2的判断，直到根结点；如果向上推算过程中发现了失衡的现象，则进行步骤 4；
如果其父结点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根结点的树的高度发生变化，则继续进行步骤2的检索推算； 如果与原来以父结点为根结点的高度⼀致时，则可说明父结点的父结点及祖先结点的平衡因子将不会有变化，因此可以退出处理

4.2删除结点有左子树或右子树

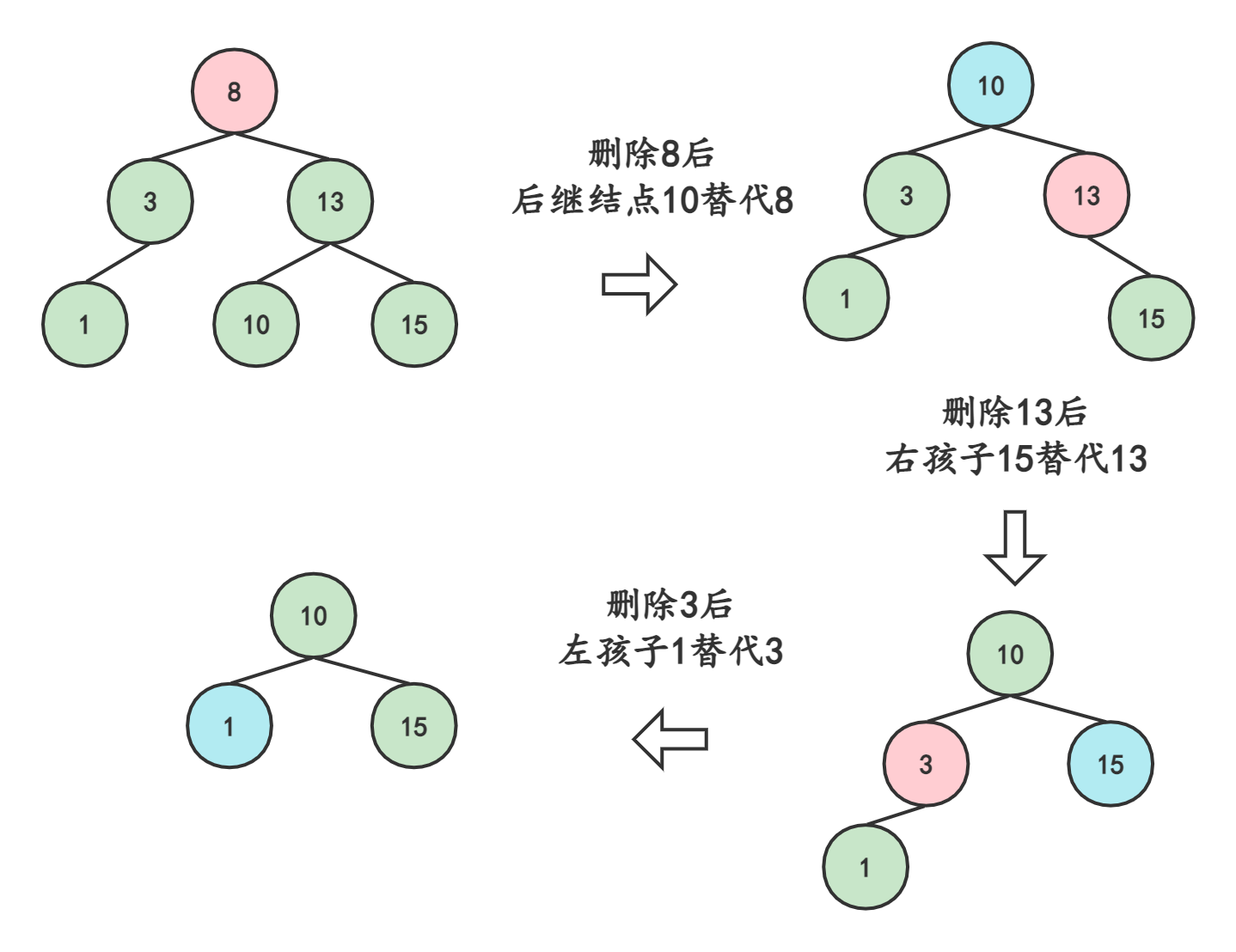
将左子树（右子树）替代原有结点8的位置
结点8被删除后，则以8的父结点13为起始推算点，依此向上检索推算各节点（父、祖先）是否失衡
如果其父结点未失衡，则继续向上检索推算其父节点的父结点是否失衡…如此反复步骤2的判断，直到根结点 ；如果向上推算过程中发现了失衡的现象，则进行步骤4的处理
如果其父结点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父结点为根结点的树的高度发生变化，则继续进行步骤2的检索推算； 如果与原来以父结点为根结点的高度⼀致时，则可说明父结点的父结点及祖先结点的平衡因子将不会有变化，因此可以退出处理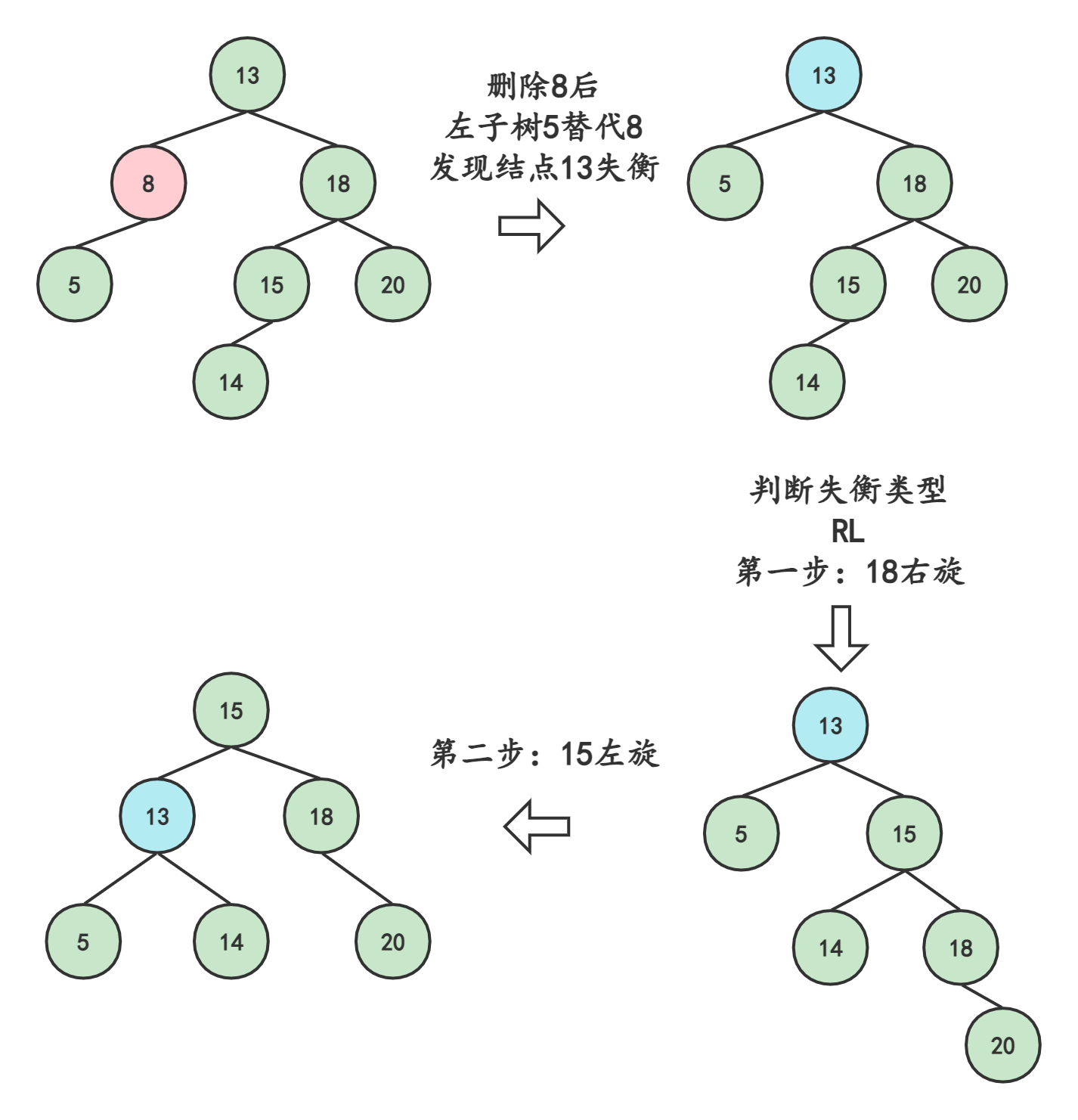

4.3删除结点有左右子树

找到被删结点10和替代结点 9 (结点10 的前继结点或后继结点 ——此处选择前继)
将替代结点9 的值赋给结点 10 ，再把替代结点9的左孩子7替换替代结点9的位置
以9的父结点 6为起始推算点，依此向上检索推算父结点或祖先结点是否失衡
如果其父结点未失衡，则继续向上检索推算其父节点的父节点是否失衡…如此反复③的判断，直到根结点；如果向上推算过程中发现了失衡的现象，则进行⑤的处理
如果其父节点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。 如果平衡化处理结束后，发现与原来以父节点为根节点的树的高度发⽣变化，则继续进行 ② 的检索推算；如果与原来以父结点为根结点的高度⼀致时，则可说明父节点的结节点及祖先结点的平衡因子将不会有变化，因此可以退出处理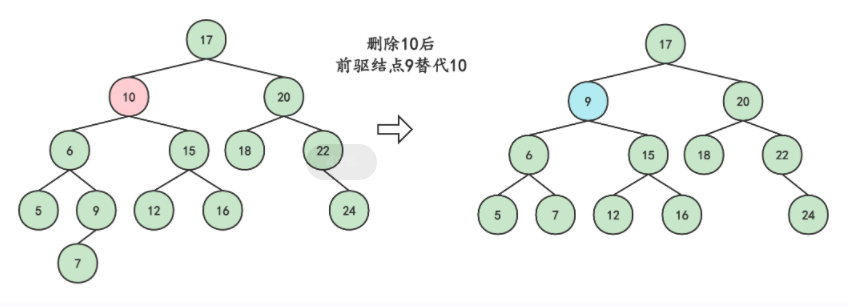

6.1LL

6.2RR

6.3LR

6.4RL