2024年12月25日一稿
2025年 1月 8日二稿
2025年 1月10日三稿
2025年 1月11日四稿
人生赢家
🐰6.1 图的基本概念🎓
🍒6.1.1 图的定义和表示🌼
图是由一些 顶点 和连接这些顶点的一些 边 所组成的离散结构。
图的 V 不能是空集，E 可以是空集（一个图可以只有一点）
相邻和邻接 性质 无向图 有向图 相邻 点 + 边 边 邻接 点
握手定理一（无向图）
D = 2 * | E | (无向图 / 有向图)
握手定理二（有向图）
D = 2 * | E | (无向图 / 有向图)
并且对于有向图，入度之和 = 出度之和 = E
出就是“ + ”，入（...）就是“ - ”
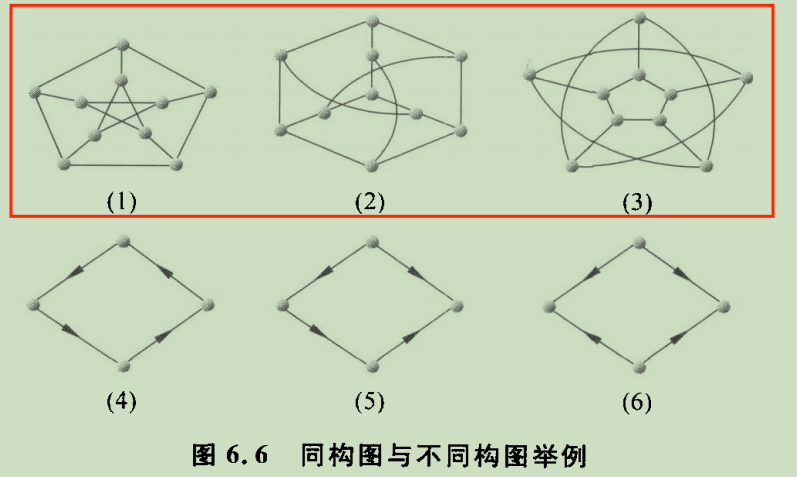
🍒6.1.2 图的同构🌼
顶点之间的关系
🍒6.1.3 完全图与正则图🌼
🍒6.1.4 子图与补图🌼
🍒6.1.5 通路与回路🌼
🐰6.2 图的连通性 𝐺𝑟𝑜𝑤 𝑓𝑙𝑜𝑤𝑒𝑟𝑠
🥩6.2.1 无向图的连通性 💣 ˎˊ˗
🥩6.2.2 有向图的连通性 💣 ˎˊ˗
🐰6.3 图的矩阵表示🍭🥑
🍍6.3.1 关联矩阵📚
🍍6.3.2 有向图的邻接矩阵📚
🍍6.3.3 有向图的可达矩阵📚
🐰6.4 欧拉图🌹🥑
🐰6.5 哈密顿图🌹🥑
🐰6.6 二部图🌹🥑
🎄6.6.1 二部图及判别定理🤞🏻
🎄6.6.2 完备匹配🤞🏻
🐰6.7 平面图🌹🥑
🏃🏻 6.7.1 平面图及其判定定理🍻
🏃🏻6.7.2 平面图的对偶图🍻
🐰6.8 带权图🌹🥑
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
