数据结构要点总结——07 模式匹配算法（包含KMP）！！重点

1.朴素模式匹配算法

       子串的定位操作通常称做串的模式匹配（其中称为模式串），是各种串处理系统中最重要的操作之一。顺便提一嘴，本小节中的串均采用 定长顺序存储结构，这一点将用于代码编写。

朴素模式匹配算法 的 基本思想 是： 将主串（长度为n）中所有长度为m的子串依次与模式串依次对比，直到找到一个完全匹配的子串或所有的子串都不匹配为止。

最多匹配n-m+1个字串。

最坏时间复杂度O(nm)

其算法如例(实际代码见本章末尾)：

int Index(SString S, SString T. int pos) { //返回子串 在主串 中第 pos 个字符之后的位置。若不存在，则函数值为0,其中，T非空，1<=pos<= StrLength(S)
      i=pos; 
      j=l; 
      while (i <= s[o] &.&. j <= T[O]) { 
           if (S[i] = = T[j]) {
                ++ i; 
                ++ j; 
              } //继续比较后继字符
           else { 
                i = i - j + 2 ; 
                j = 1 ; 
              } //指针后退重新开始匹配
      if (j > T[O]) 
           return i-T[O]; 
      else 
           return O ; 
} 

 2.改进算法（KMP）

此算法可以在 O(n+m) 的时间内完成匹配操作，改进在于：每当一趟匹配过程中出现字符比较不等时，不需回溯指针，而是利用已经得到的”部分匹配＂的结果将模式向 右＂滑动“尽可能远的一段距离后，继续 进行比较。

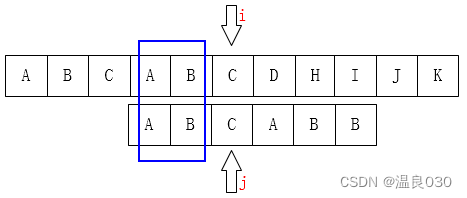
我们发现，模式串是向后滑行的一段距离在进行匹配了，掠过了字符串的ABC三个字节。这一点我们人眼可以直接看出，可是怎么告诉计算机要滑行多远呢？

我们可以使用一个数组来告诉计算机，当模式串的某个字符不匹配时，模式串指针j需要回溯到哪，这个数组就叫做 next数组： 当模式串的第n个字符不匹配时，令模式串跳到next[n]的位置再继续匹配。

串的前缀:包含第一个字符，且不包含最后一个字符的子串
串的后缀:包含最后一个字符，且不包含第一个字符的子串

当第j个字符匹配失败，由前 1~j-1 个字符组成的串记为S，

则: next[j]=s的最长相等前后缀长度+1 特别的，规定next[1]=0（这样j++之后为1）next[1]可以无脑填1

例：

模式串	A	B	A	B	A	A
next数组	0	1	1	2	3	4

当第1个字符A匹配失败时，S为 '  ' ,next[1]=0

当第2个字符B匹配失败时，S为 'A' ,next[2]=s的最长相等前后缀'  '长度0   + 1 = 1

当第3个字符A匹配失败时，S为 'AB' ,next[3]=s的最长相等前后缀'  '长度0   + 1 = 1

当第4个字符B匹配失败时，S为 'ABA' ,next[4]=s的最长相等前后缀'A'长度1   + 1 = 2

当第5个字符C匹配失败时，S为 'ABAB' ,next[5]=s的最长相等前后缀'AB'长度2   + 1 = 3

当第6个字符C匹配失败时，S为 'ABABA' ,next[6]=s的最长相等前后缀'ABA'长度3   + 1 = 4

3.KMP改进算法

       如上的'ABABAA'模式串对应的next数组，我们发现，当第三个字符不匹配时，模式串指针会回溯到模式串第一个字符的位置，但是第一个字符和第三个字符都是A，所以其实可以直接跳到和第一个字符串不匹配的情况。

对于这样的情况可以通过对next改进为 nextval数组：

模式串	A	B	A	B	A	A
next	0	1	1	2	3	4
nextval	0	1	0	1	0	4

像nextval中第六个字符的A， 回到4的位置，但是4的位置为B，所以不可以继续简化。

大家只要会求next数组，基本上就会求nextval数组，考试也只会考简单的nextval求算问题，接下里的代码展示也只展示朴素匹配和KMP算法，改进KMP就不展示了。

4.朴素模式匹配算法、KMP代码展示

#include <stdio.h>
#include <string.h>

// 朴素模式匹配  (注意，如果你没有定义字符串结构string ，这里是不可以使用的，c语言不自带string结构，所以用char)
int naiveMatch(char *S, char *T) {
    int n = strlen(S);//获取字符串长度   strlen需要常量字符串 因此使用char *S  char *T  
    int m = strlen(T);//获取模式串长度   带*代表指向字符串的指针，强调的是字符串 
    int num=0; 
    for (int i = 0; i <= n - m; i++) {
        int j;
        for (j = 0; j < m; j++) {
            if (S[i + j]!= T[j]) {
            	num++;
                break;//子串中有一个字符同模式串不同就跳出当前子串匹配 
            }
            num++;
        }
        if (j == m) {//如果满足此条件，说明j++到了m,也就是子串与模式串匹配字符的长度等于模式串长度，两串相等 
            printf("朴素模式匹配共%d次匹配  \n", num); 
            return i;
        }
    }
    printf("朴素模式匹配共%d次匹配  \n", num);
    return -1;
}


// 计算 next 数组  考研一般只要求你手动能算出就可以 
void getNext(char * T, int next[]) {
    int m = strlen(T);
    int i = 1, j = 0;
    next[1] = 0;
    printf("NEXT数组为： ");
    printf("%d ",next[1]);
    while (i < m ) {
        if (j == 0 || T[i-1] == T[j-1]) {//char字符串从0开始的，next从1开始的  所以-1 
            ++i;
            ++j;
            next[i] = j;
            printf("%d ",next[i]);
        } else {
            j = next[j];
        }
    }
     printf("\n");
}

// KMP 匹配算法
int kmpMatch(char *S, char *T) {
    int n = strlen(S);
    int m = strlen(T);
    int num=0; 
    int next[m+1];
    getNext(T, next);
    int i = 1, j = 1;
    while (i <=n && j <= m) {
        if (j == 0 || S[i-1] == T[j-1]) {
            ++i;
            ++j;
            
        } else {
            j = next[j]; 
        }
        num++; 
    }
    if (j > m) {
    	printf("KMP匹配共%d次匹配  \n", num); //这里应该是出错了  大家自己找一找 
		//次数不太对 我口算是18次匹配 
        return i-m-1;
    } else {
        return 0;
    }
}







int main() {
    char S[] = "ABABCCABCABABAABC";
    char T[] = "ABABAA";
    printf("字符串：%s\n",S); 
    printf("模式串：%s\n",T); 
    printf("\n");
    
    int index1 = naiveMatch(S, T);
    if (index1!= -1) {
        printf("朴素模式匹配  模式串在文本中的起始位置: %d\n", index1);
        printf("\n");
    } else {
        printf("朴素模式匹配未找到匹配模式\n");
    }
    
    int index2 = kmpMatch(S, T);
    if (index2!= -1) {
        printf("KMP匹配  模式串在文本中的起始位置: %d\n", index2);
        printf("\n");
    } else {
        printf("KMP未找到匹配模式\n");
    }

    return 0;
}

累死了  不写了。。。。。。。