文章目录
前言
DoRA 将预训练的权重分解为幅度和方向两个部分进行微调,具体来说,使用 LoRA 进行方向更新,以有效地最小化可训练参数的数量。通过采用 DoRA,我们增强了 LoRA 的学习能力和训练稳定性,同时避免了任何额外的推理开销。在对 LLaMA、LLaVA 和 VL-BART 进行微调方面,DoRA 在各种下游任务(例如常识推理、视觉指令调整以及图像/视频文本理解)上始终优于 LoRA
一、简介
使用广泛的通用领域数据集进行预训练的模型已展现出卓越的泛化能力,显著惠及从NLP任务到多模态任务等众多应用。为了使这些通用模型能够适应特定的下游任务,通常采用完全微调 (FT) 方法,即重新训练所有模型参数。然而,随着模型和数据集规模的扩大,对整个模型进行微调的成本变得非常高昂
1.1背景
-
参数高效微调(PEFT):大模型全参数微调(Full Fine-Tuning, FT)成本高昂。主流方法如 LoRA 通过低秩矩阵更新权重(ΔW=BAΔW=BA),避免推理延迟,但存在精度差距
-
关键问题:LoRA 与 FT 的性能差异通常归因于可训练参数量不足,但论文发现 更新模式差异 是更深层原因
1.2核心发现
通过 权重分解分析:
-
FT 更新模式:权重方向(Direction)与幅度(Magnitude)的变化呈 负相关(ΔD↑⇒ΔM↓)
-
LoRA 更新模式:方向与幅度变化呈 正相关(ΔD↑⇒ΔM↑)这限制了 LoRA 的细粒度调整能力,导致性能不如 FT

二、PRFT与LoRA variants
自适应网络性能测试 (PEFT) 方法旨在降低微调大规模模型的高昂成本。它们通过训练相对于参数总数相对较小的参数子集来适应下游任务,从而实现这一点
现有的 PEFT 方法可分为三类
①第一类称为基于适配器的方法,这类方法在原始冻结的主干网络中引入额外的可训练模块。例如,(Houlsby et al., 2019) 建议按顺序将线性模块添加到现有层,而 (He et al., 2021) 则主张将这些模块与原始层并行集成以增强性能
②第二类是基于提示的方法。这些方法在初始输入中添加额外的软标记(提示),并专注于微调这些可训练向量。然而,这些方法通常由于对初始化的敏感性而面临挑战,从而影响其整体有效性。前两类方法,无论是改变模型的输入还是架构,都会导致推理延迟与基线模型相比增加
③LoRA以及相关变体其变体属于第三类 PEFT,显著特点是不会增加任何额外的推理负担。这些方法在微调过程中应用低秩矩阵来近似权重变化,并可以在推理之前与预训练权重合并
如:(Zhang et al., 2023) 采用 SVD 分解,并修剪不太重要的奇异值以实现更高效的更新;(Hyeon-Woo et al., 2022) 专注于联邦学习的低秩 Hadamard 积;Qiu et al., 2023) 在微调扩散模型中利用正交因式分解。(Renduchintala et al., 2023) 使用权重绑定来进一步减少可训练参数。 (Yeh 等人,2023) 引入了一个统一的 LoRA 家族框架,用于稳定传播。(Ponti 等人,2022) 从具有路由功能的 LoRA 库中选择不同的 LoRA 组合,用于不同的任务。(Kopiczko 等人,2024) 实现了可学习的缩放向量,用于调整跨层的共享冻结随机矩阵对
三、LoRA和FT的模式分析
3.1 . Low-Rank Adaptation
基于微调过程中的更新会表现出较低的“固有秩”这一假设,提出使用两个低秩矩阵的乘积来逐步更新预训练权重。对于预训练权重矩阵 W0 ∈ Rd×k,LoRA 利用低秩分解对权重更新 ∆W ∈ Rd×k 进行建模,表示为 BA,其中 B ∈ Rd×r和 A ∈ Rr×k表示两个低秩矩阵,且 r ≪ min(d, k)
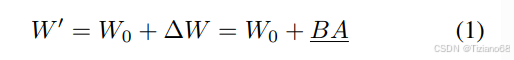
其中,W0 在微调过程中保持不变,下划线所示的参数正在进行训练。矩阵 A 初始化为均匀 Kaiming 分布,B 初始设置为零,因此∆W = BA 在训练开始时为零。值得注意的是,∆W 的这种分解可以用其他 LoRA 变体替代。此外,基于公式 (1),我们可以将学习到的 ∆W 与预训练权重 W0 合并,并在部署前获得 W′。鉴于 W′ 和 W0 均落在 Rd×k 的维度范围内,因此与原始模型相比,LoRA 及其相关变体在推理过程中不会引入任何额外的延迟
3.2 权重分解分析
LoRA 中的研究表明,LoRA 可以被视为完全微调的近似值。通过逐步提高 LoRA 的秩 r,使其与预训练权重的秩保持一致,LoRA 可以达到与FT类似的表达能力。因此,许多先前的研究将 LoRA 和 FT 之间的准确率差异主要归因于可训练参数数量有限,且通常无需进一步分析。受权重归一化的启发,该技术将权重矩阵重新参数化为幅值和方向,以加速优化,我们引入了一种创新的权重分解分析方法。将权重矩阵重构为两个独立的部分:幅度和方向,以揭示 LoRA 和 FT 学习模式的内在差异
3.2.1 分析方法
考察 LoRA 和 FT 权重相对于预训练权重的幅度和方向的更新,以揭示两者学习行为的根本差异。W ∈ Rd×k的权重分解可以表示为:
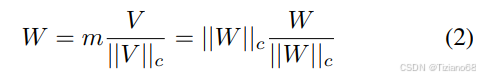
其中 为幅值向量,
为方向矩阵,
为矩阵每列的向量范数。这种分解确保
的每一列仍然是单位向量,并且 m 中对应的标量定义了每个向量的幅值
使用公式 (2) 分解查询/值权重矩阵的预训练权重 、完整微调权重
和合并后的 LoRA 权重
。W0 和 WFT 之间的幅度和方向变化可以定义如下:
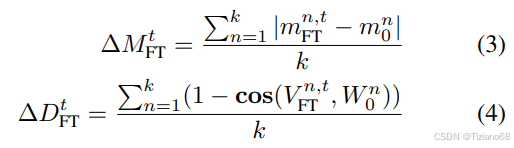
与
分别表示在第 t 个训练步骤中
和
之间的幅度差异和方向差异,
cos(·, ·) 为余弦相似度函数。 和
是其各自幅度向量中的第 n 个标量,而
和
是
和
中的第 n 列。
和
之间的幅度差异和方向差异的计算方法类似,分别按照公式 (3) 和公式 (4) 进行。从四个不同的训练步骤中选择检查点进行分析,包括 FT 和 LoRA 的三个中间步骤和一个最终检查点,并对每个检查点进行权重分解分析,以确定不同层中的∆M 和∆D
3.2.2 Analysis Results
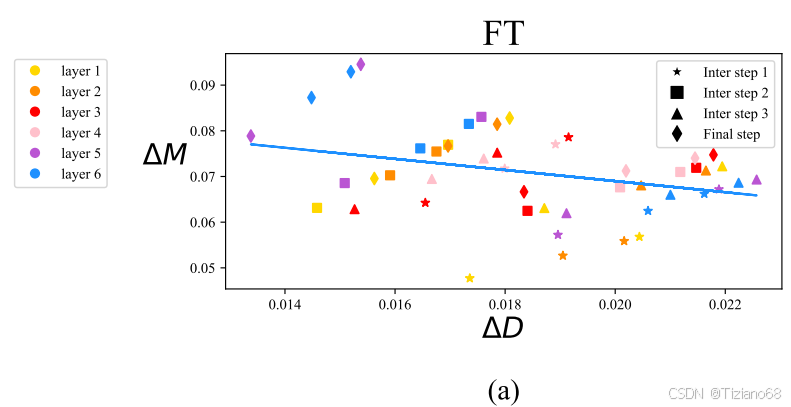
图 2 (a) 和 (b) 展示了 FT 和 LoRA 查询权重矩阵的变化,每个点代表来自不同层和训练步骤的查询权重矩阵的 (∆Dt, ∆Mt) 对。值得注意的是,LoRA 在所有中间步骤中都呈现出一致的正斜率趋势,表明方向和幅度的变化之间存在比例关系。相比之下,FT 则表现出更加多样化的学习模式,斜率相对较负。FT 和 LoRA 之间的这种区别可能反映了它们各自的学习能力。
虽然 LoRA 倾向于按比例增加或减少幅度和方向的更新,但它缺乏进行更细微调整的精准能力。具体而言,LoRA 无法熟练地执行轻微的方向变化以及更显著的幅度变化,反之亦然,而这正是 FT 方法的典型特征。我们怀疑 LoRA 的这种局限性可能源于同时学习幅度和方向适应性的挑战,这对于 LoRA 来说可能过于复杂。因此,在本研究中,我们旨在提出一种 LoRA 的变体,其学习模式与 FT 更为相似,并且可以提升 LoRA 的学习能力
四、Method
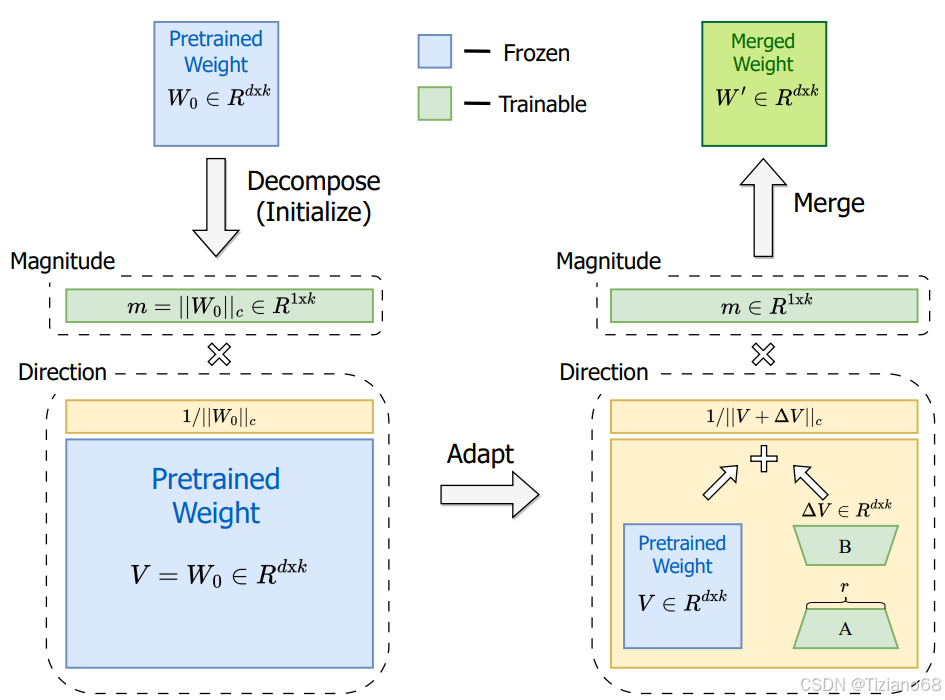
基于我们对权重分解的分析,引入DoRA。DoRA 首先将预训练的权重分解为幅度和方向分量,并对两者进行微调。由于方向分量的参数数量较大,我们进一步使用 LoRA 对其进行分解,以便进行高效的微调
4.1 权重分解低秩自适应
直觉有两个方面:
首先,我们认为,与原始方法相比,将 LoRA 限制为专注于方向自适应,同时允许幅度分量进行调整,可以简化任务,因为原始方法要求 LoRA 同时学习幅度和方向的调整。
其次,通过权重分解,优化方向更新的过程更加稳定。需要强调的是,DoRA 与权重正则化 (Salimans & Kingma, 2016) 的主要区别在于它们的训练方法。权重归一化会从头开始训练两个组件,这使得该方法对不同的初始化方法敏感。相反,DoRA 避免了此类初始化问题,因为两个组件都从预训练的权重开始。我们用预训练的权重 W0 初始化 DoRA,如公式 (2) 所示,其中 m = ||W0||c,初始化后 V = W0。然后,我们保持 V 不变,并将 m 设为可训练向量。然后,方向分量通过 LoRA 进行更新。DoRA 的公式与公式 (1) 类似,为:
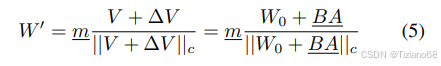
其中 ∆V 是通过乘以两个低秩矩阵 B 和 A 而学到的增量方向更新,下划线参数表示可训练参数。矩阵 B ∈ Rd×r和 A ∈ Rr×k的初始化符合 LoRA 的策略,以确保在微调之前 W′等于 W0。此外,DoRA 可以在推理之前与预训练权重合并,从而不会引入任何额外的延迟
4.2 DoRA梯度分析
在本节中,我们首先推导 DoRA 的梯度,并说明我们提出的分解方法如何有利于 ∆V 的优化。随后,我们从梯度的角度进行分析,以阐明 DoRA 的学习模式,即其倾向于呈现负斜率
从公式 (5) 中,我们可以得到 Loss 关于 m 和 V 的梯度V′ = V + ∆V=,其表达式为:
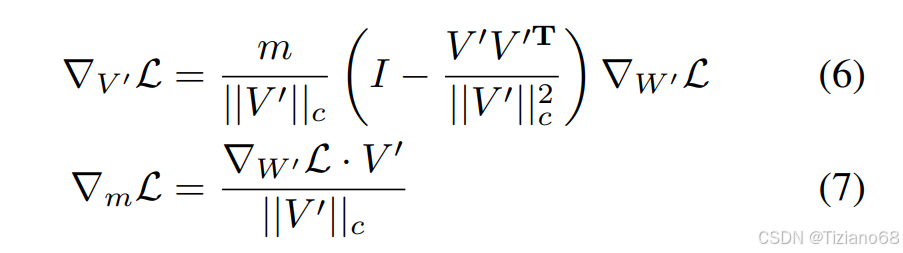
4.2.1 方向梯度:

4.2.2 梯度推导(式6)


等式 (6) 表明,权重梯度 ∇W′L 经过 m/||V||c 缩放,并向外投影,远离当前权重矩阵。这两个效应有助于使梯度的协方差矩阵与单位矩阵更加接近,这有利于优化
4.2.3 幅度梯度:
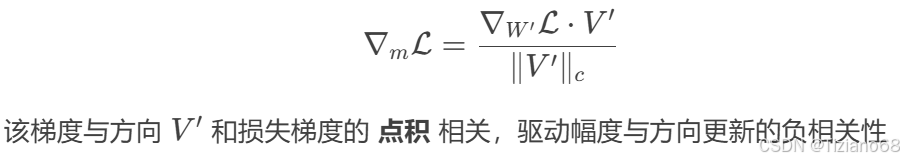
此外,假设 V′ = V + ∆V ,梯度 等价于
。这种分解带来的优化优势完全转移到 ∆V ,提高了 LoRA 的学习稳定性。
在接下来的讨论中,用小写字母表示向量,而不是以前的矩阵形式符号。考虑 作为权重向量的参数更新,其中
。
在两个假设的更新场景 S1 和 S2 中,S1 涉及较小的方向更新 (),而 S2 涉及较大的方向更新 (
)。假设
,在时刻 0,有∆v = 0 且 v′ = v。由
<
,可知
。
由于,因此
。根据 4.1 节,设 v 初始化为 v0,且 w′ = w0,在时刻0,有
。利用∆v = 0 时的余弦相似方程:
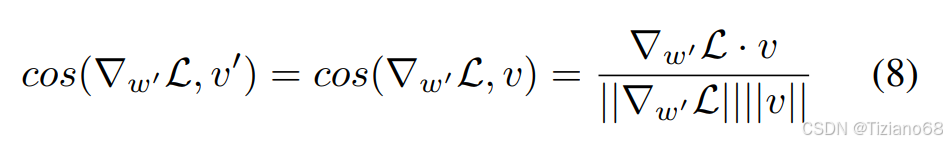
4.2.4 负相关机制(式9–10)
设 m∗ 为向量 w ′ 的幅值标量则公式 (7)关于 m∗ 可改写为:
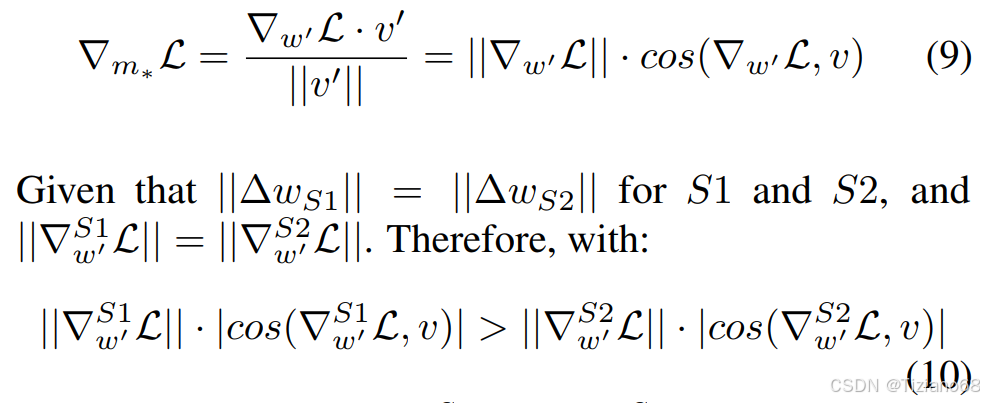
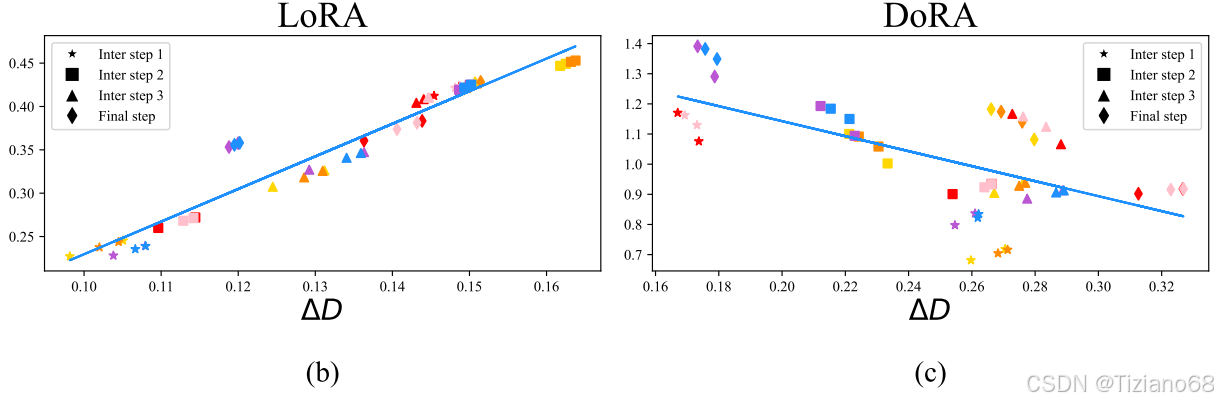
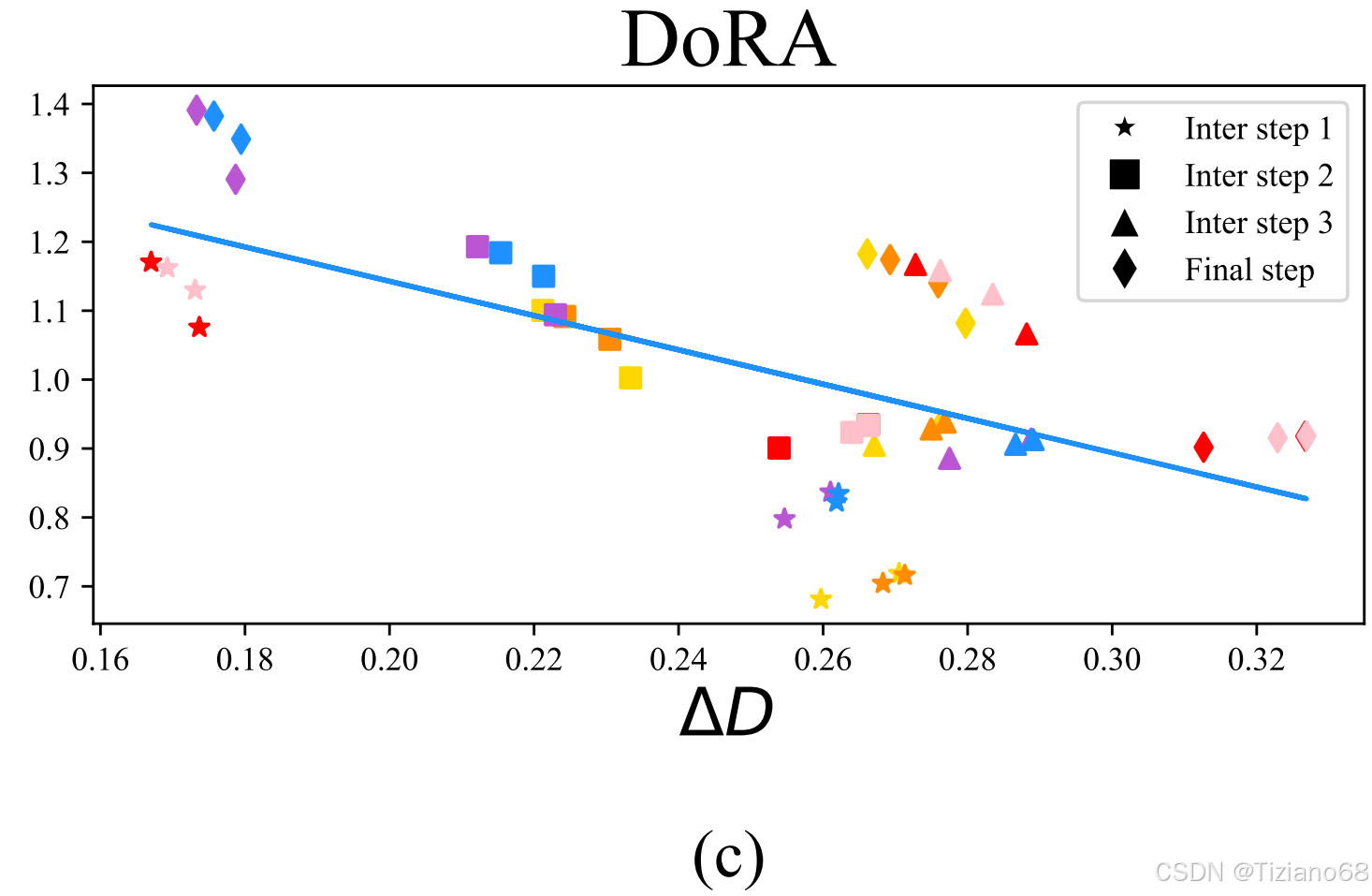
可以推断 ,这表明S1 的幅度更新大于 S2,而方向性改变小于 S2。我们的结论在实践中普遍成立,如图 (c) 所示。因此,我们有效地展示了如何利用 DoRA 来调整学习模式,使其与 LoRA 的学习模式有所不同,并更接近于 FT 的学习模式

4.3 减少训练开销
在等式 (1) 中,W′和 ∆W 的梯度相同。然而,对于 DoRA,它将低秩自适应重定向到方向分量,低秩更新的梯度与 W′ 的梯度不同,如等式 (6) 所示。这种发散需要在反向传播过程中占用额外的内存。为了解决这个问题,我们建议将等式 (5) 中的 ||V + ∆V ||c 视为常数,从而将其从梯度图中分离出来。这意味着虽然 ||V + ∆V ||c 动态地反映了 ∆V 的更新,但它在反向传播过程中不会接收任何梯度。经过此修改,相对于 m 的梯度保持不变,∇V ′L 被重新定义为:


这种方法显著降低了梯度图的内存消耗,且准确率没有显著差异
五、物理意义分析


总结
权重分解分析:揭示 FT 与 LoRA 的更新模式差异(方向-幅度负相关 vs 正相关)
DoRA 方法:
解耦幅度与方向优化,方向更新由 LoRA 高效实现
梯度投影机制提升训练稳定性
零推理开销:权重可合并,与 LoRA 兼容





















 1273
1273

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








