完全背包---java小知识

💬推荐一款模拟面试、刷题神器，从基础到大厂面试题👉点击跳转刷题网站进行注册学习

---

前言

`背包问题分为：01背包，完全背包以及多重背包，本文主要讲解完全背包。
01背包以及01背包的优化讲解：
01背包：https://blog.youkuaiyun.com/m0_55486529/article/details/123806820
01背包优化：https://blog.youkuaiyun.com/m0_55486529/article/details/123831655

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、完全背包是什么？

完全背包的物品数量是没有限制的，而01背包的物品个数为一，所以完全背包与01背包最大的区别就是物品数量不同。

二、解题技巧

题目：有5个物品，背包的容量为10。求放入背包的最大价值

01背包推导：

完全背包推导：

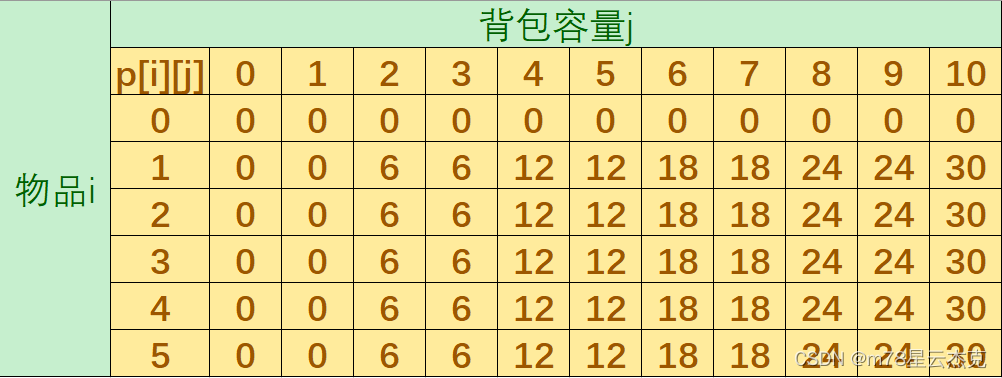
因为恰巧第一个重量小，且价值高，所以推导不明显，我们把第一个价值改为2.（仅仅为了展示推导过程更明显）

0-1背包状态转移方程：
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]）
完全背包状态转移方程：
f[i][j]=max(f[i-1][j],f[i][j-w[i]]+v[i])
为什么一个是i-1，一个是i呢？
因为01背包物品个数为一，假设此时推导第i个物品，我们以i-1行作为递推依据，那么我们可以保证第i个物品只放入一次，如果我们以第i行作为递推依据，那么我们是在前面放入过i物品的前提下放入物品（当i=1时，第一个物品，j=2时我们放入一个，此时价值为6，j=4时我们又放入一个是在前一个的基础之上，价值为12）。

1.二维数组dp[][]代码

代码如下（示例）：

public class test {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		System.out.println(bagkiller(w,v,10));
	}
	public static int bagkiller(int[] w,int[] v,int n) {
		int [][] dp=new int[w.length+1][n+1];
		for (int i=1;i<=w.length;i++) {   
			for (int j=1;j<=n;j++) {
				if(j<w[i-1]) //装不下 
					dp[i][j]=dp[i-1][j]; //就等于i-1件物品容量等于j时候的价值 
				else
					dp[i][j]=Math.max(dp[i-1][j],dp[i][j-w[i-1]]+v[i-1]);//装得下分为两种情况1.装 2.不装
			}
		}
		return dp[w.length][n];
	}
}

结果：

30

2.一维数组

完全背包一维数组的原理和01背包的一维原理差不多，只不过01背包是倒推，而完全背包是正推，（因为完全背包，下一次推导只与本次数组前面有关，而01背包是以上一次推导结果有关，倒推前一次的数据不会被后一次覆盖）
代码如下（示例）：

public class test {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		System.out.println(bagkiller(w,v,10));
	}
	public static int bagkiller(int[] w,int[] v,int n) {
		int [] dp=new int[n+1];
		for (int i=0;i<w.length;i++) {   
			for (int j=w[i];j<=n;j++) {  //j只有大于等于w[i]才能放入i物品
					dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]);
			}
		}
		return dp[n];
	}
}

---

总结

以上就是今天要讲的内容，如果不太理解建议自己画一遍表格。