X32专项练习部分26

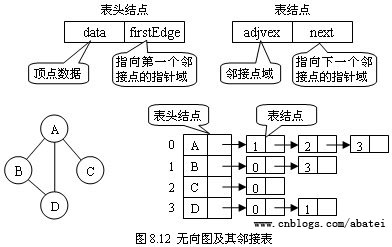
邻接表表头向量大小

/*
    对于一个具有n个顶点的无向图
    若采用邻接表表示，则表头向量的大小为()
        正确答案: A
        n
        n+1
        n-1
        n+边数

    实际上问的就是一共有几个表头
    表头向量的大小等于顶点的数量
    每个顶点建立1个单链表
     */

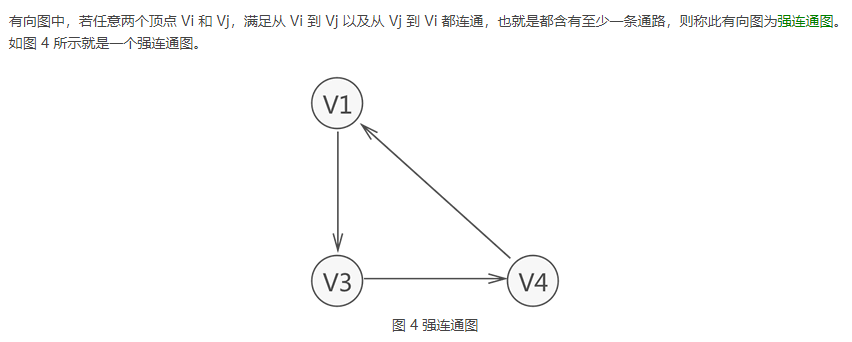
强连通图和连通图

/*
    设某强连通图中有 n 个顶点，则该强连通图中 至少有（）条边。

        正确答案: C
        n(n-1)
        n+1
        n
        n(n+1)

    强连通图中有n个顶点，当存在一个环时，需要的边的数目是最少的，所以有n个顶点的环最少需要n条边
    下面补充以下强连通图和连通图的定义
     */

• 强连通图
  
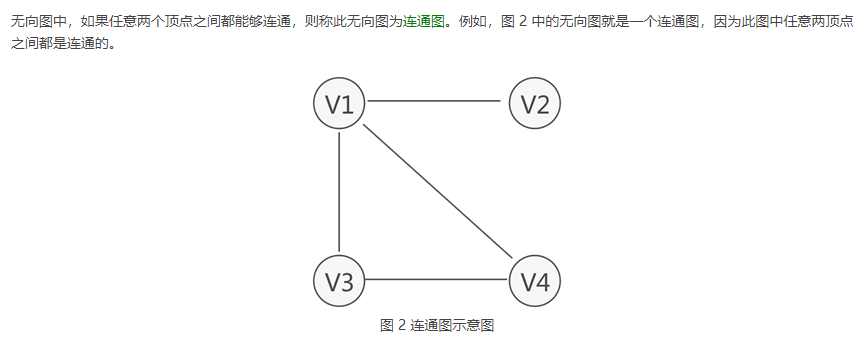
• 连通图
  
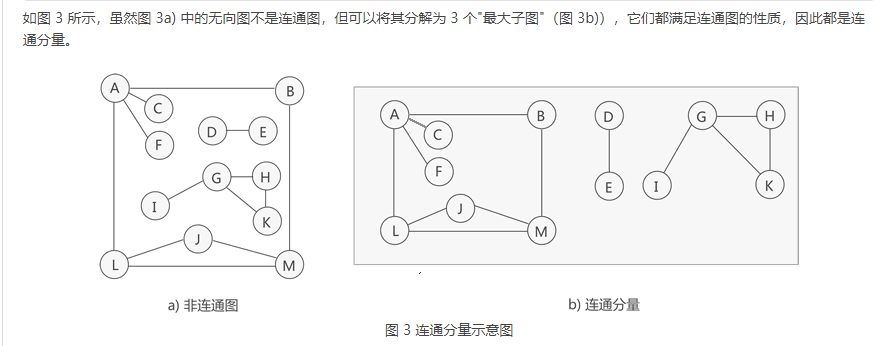
• 非连通图和连通分量
  

求平衡二叉树的节点总数

/*
    若平衡二叉树的高度为6，且所有非叶结点的平衡因子均为 1，则该平衡二叉树的结点总数为

        正确答案: B
        12
        20
        32
        33

    平衡因子是左子树高度 - 右子树高度
    斐波那契数列，平衡二叉树的最小结点数：f(n)=f(n-1)+f(n-2)+1
    公式验证就不写了

    其中f(1)=1,f(0)=0
    括号中的数代表深度
    从下往上数：
    深度为2时，f(2)=f(1)+f(0)+1=2
    f(3)=f(2)+f(1)+1=4
    依此类推  f(4)=7,f(5)=12,f(6)=20

    如果求叶子节点
    就用f(6) - (f(5) + f(4) + f(3) + f(2) + f(1))
     */

邻接矩阵判断有边的时间复杂度

/*
    用邻接矩阵存储有n个结点(0,1,...,n)和e条边的有向图(0≤e≤n(n-1))
    判断结点i，j（0≤i，j≤n-1）有边的时间复杂度是（）

        正确答案: A
        O(1)
        O(n)
        O(e)
        O(n+e)

    既然是邻接矩阵
    判断是否有边就是判断A[i][j]对应的值是否为1
    数组下表代表节点序号，直接将点i,j带入
    时间复杂度为O(1)
     */

有向图缩短工期

/*
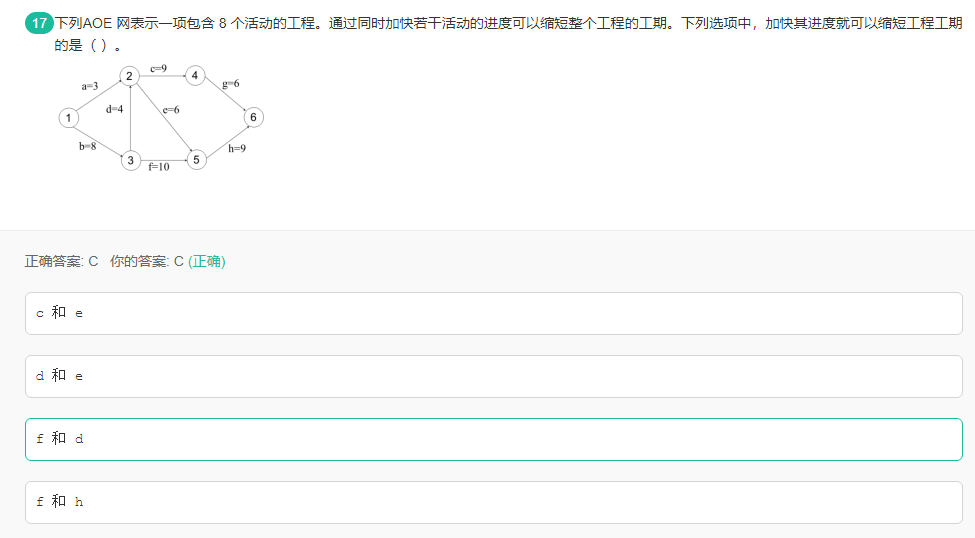
    首先查看关键路径
    关键路径是指所有1 -> 6
    的路径集合
    b,d,c,g
    b,d,e,h
    b,f,h

    再根据选项
    不管走哪一条路径
    降低f,d的路径必然缩短全部工期
    故选C
     */

斐波拉契数列的时间复杂度

/*
    以下计算斐波那契数列的函数时间复杂度为()
    int Fibonacci(int n) {
       if(n==0)
         return 0;
       else if(n==1)
         return 1;
       else
         return Fibonacci(n-1)+Fibonacci(n-2)
    }

                        f(10)
                 /                \
                f(9)              f(8)
            /         \        /       \
          f(8)       f(7)   f(7)      f(6)
        /    \      /     \
     f(7)  f(6)  f(6)     f(5)

     假设树的深度为n
     计算复杂度：
     2^0+2^1+2^2+.....2^n = O(2^n)

	所以在数据量非常庞大的时候，程序会计算很长一段时间
     */

两层循环时间复杂度

/*
    下列程序的时间复杂度是
    count = 0;
    for (int k = 1; k <= n; k *= 2)
        for (int j = 1; j <= n; j++)
            count++;

        O(log(n))
        O(n)
        O(nlog(n))
        O(n^2)

    内层循环条件j<=n与外层循环的变量无关
    每次循环j自增1，每次内层循环都执行n次
    外层循环条件为k<=n，增量定义为k*=2
    循环次数(t)1，k=2
    循环次数(t)2，k=4
    循环次数(t)3，k=8
    可知循环次数为2^t<=n，即t<=log2n

    所以内层循环的时间复杂度是O(n)，外层循环的时间复杂度是O(log2n)
    对于嵌套循环，根据乘法规则可知
    该段程序的时间复杂度T(n)=T1(n)*T2(n)=O(n)*O(log2n)=O(nlog2n)
    选C
    
    所以这种题就是的时间复杂度就是每层循环的乘积
     */

逆拓扑结构

/*
    用DFS遍历一个无环有向图，并在DFS算法退栈返回时打印相应的顶点
    则输出的顶点序列是( )

        正确答案: A
        逆拓扑有序
        拓扑有序
        无序的
        无法确定

    用DFS(深度优先遍历)遍历无环有向图
    沿着一条边一直向下搜索
    每搜索1个顶点压入栈中
    所以搜索路径是1条弧
    搜索到最后1个被访问的节点
    开始弹栈

    最后栈输出的元素是第1个被访问的元素
    所以是逆拓扑结构
     */

总目录