衍射受限非相干成像系统的传递函数

相干光照明时: 物面上各点的振幅和相位随时间作相同的变化, 彼此相关(相干). 它们发出的光波之间的相位差仅由相对位置决定, 相位差恒定. 在像面上的光场分布是复振幅的线性叠加.

非相干照明时: 在观测时间内, 物面上各点的振幅, 相位随时间变化的方式是彼此独立、统计无关的. 非相干成像系统是强度的线性系统. 在一定条件下是强度的线性空间不变系统.

一、非相干成像系统的光学传递函数（OTF）

非相干成像系统对强度是线性空不变的, 物像的强度分布关系满足 :

式中: Ig是几何光学理想像的强度分布, Ii 是实际像的强度分布,hI为强度脉冲响应(或称非相干脉冲响应、强度点扩散函数、非相干点扩散函数)

        该式表明: 像的强度分布是几何光学理想像的强度分布与强度点扩散函数的卷积, 系统的成像特性由强度点扩散函数决定.

强度点扩散函数是点物产生的像斑的强度分布, 等于相干点扩散函数的模方:

在频域中, 可表示为：

其中:

由于Ii , Ig, hI都是强度分布, 都是非负实函数, 它们的频谱一般都是复函数, 但必有一个幅值很大的零频分量(直流分量), 即:

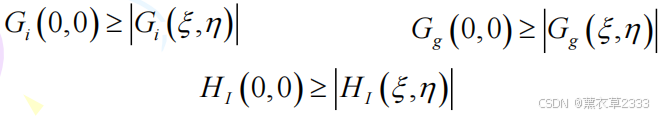
例

从图像的视觉效果考虑,更有意义的是 Gi 、Gg和HI相对于各自零频分量的比值, 即用零频分量归一化的频谱:

归一化频谱满足:

其中

是非相干成像系统的光学传递函数 (OTF), 它在频域中描述非相干成像系统的成像特性.

都可以用它的模和辐角表示:

M（，）称为调制传递函数(Modulation Transfer Function,MTF)，描述了系统对各频率分量对比度的传递特性。

（，）称为相位传递函数(Phase Transfer Function, PTF)，描述了系统对各频率分量施加的相移。

调制度的定义:

几何理想像的调制度:

实际像的调制度:

从而得到:

相位变化:

（，）: 理想像的相位分布

（，）: 相位传递函数(系统产生的相移)

若（，）= 2Π,表示错开了一个条纹;

若（，）= ,表示错开了 θ /π2 条纹.

二、OTF与CTF的关系

对同一系统来说, OTF是CTF的归一化自相关函数.

三、衍射受限系统的OTF

相干照明衍射受限系统的CTF为:

非相干照明衍射受限系统的OTF:

衍射受限系统的OTF是光瞳函数的归一化自相关函数.

3.1 OTF的几何解释

1) 分母总是光瞳的总面积

2) 分子代表中心位于(-,-)的经过平移的光瞳与原光瞳的重叠面积, 设S(,)

3) OTF是归一化的重叠面积 

重叠面积取决于两个错开光瞳的相对位置, 即和频率有关

3.2 衍射受限系统OTF的性质

(1) 由于是实的非负函数, 因此衍射受限的非相干成像系统只改变各频率余弦分量的对比度, 而不改变它们的相位.

(2) .当 =  = 0时, 两个光瞳完全重叠, 归一化重叠面积为1, 这表明理论上系统的零频分量无阻挡, 无衰减, 无相位变化, 且对比度无变化.

(3) 

这一结论很容易从两个光瞳错开后重叠的面积小于完全重叠时的面积得出. 即非零频分量的对比度一般都有所衰减.

(4) 存在截止频率. 当(,)足够大, 两光瞳完全分离时, 重叠面积为零, 此时

即在截止频率所规定范围之外的信息成分, 其OTF为零, 不能通过系统到达像面, 从而像面上不出现这些频率成分.