高精度运算

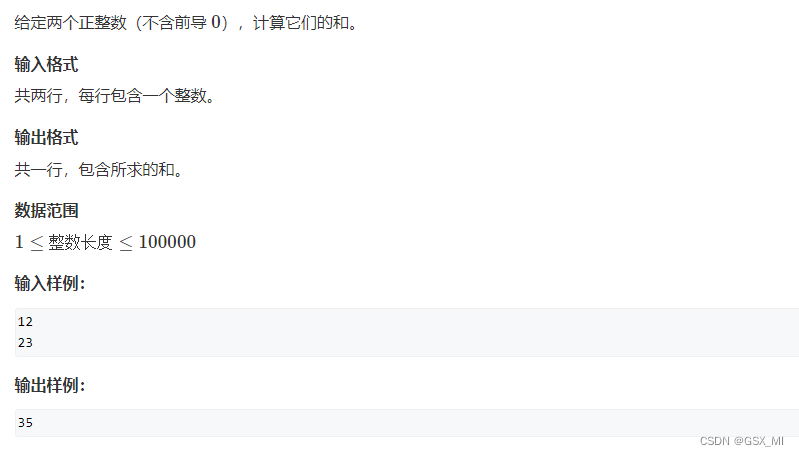
1.高精度加法

①把一个大整数存储到数组中       

②我们把大整数中的低位存到数组 arry[0] ,把最高位存储到数组的最后面

③为什么这样存储 ?

• 原因是两个数相加，相乘会产生进位，我们要在高位补上一个数 ，在一个数组中在后面添加一个数比在数组的前面添加一个数容易，在前面添加一个数字所有的数都要向后移一位。

④示例

                         

#include<iostream>
#include<vector>
#include<string>

using namespace std;

vector<int> add(vector<int>& A,vector<int>& B)
{
    int Carry = 0; //进位标志
    vector<int> res;
    
    for(int i = 0 ; i < A.size() || i < B.size() ; ++i)
    {   
        //通过判断下标i ,是否在A,B中是有效位置，一遍通过
        if(i < A.size()) Carry += A[i]; //利用进位数，不用再定义一个变量存储，妙
        if(i < B.size()) Carry += B[i];
        res.push_back(Carry % 10);
        Carry /= 10;
    }
    
    if(Carry == 1) //最后是否有进位
    {
        res.push_back(Carry);
    }
    
    return res;
    
}


int main()
{
    vector<int> A;
    vector<int> B;
    
    string str1;
    string str2;
    cin>>str1>>str2;
    
    
    //逆序插入数组
    for(int i = str1.size()-1 ; i >=0 ;--i)
    {
        A.push_back(str1[i]-'0');
    }
    
    for(int i = str2.size()-1 ; i >=0 ;--i)
    {
        B.push_back(str2[i]-'0');
    }
    
    auto C = add(A,B);
    for(int i = C.size()-1 ; i >= 0;--i)
    {
        cout << C[i];
    }
    

    return 0;
}

                        

                 

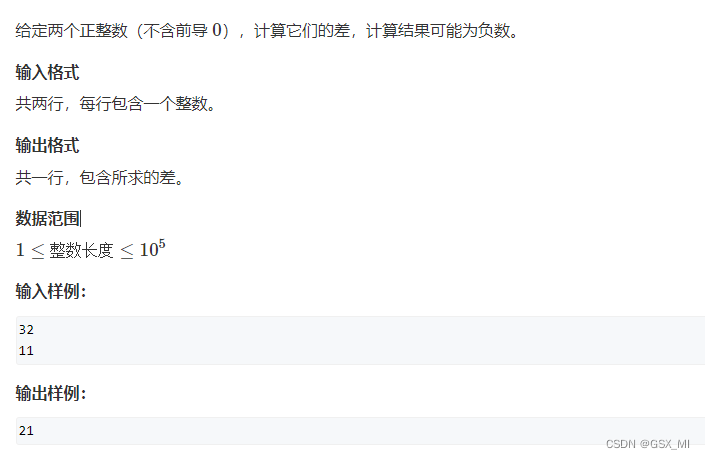
 2.高精度减法

①比较两个数的大小，如果A >= B直接相减，如果A < B , 变换成 -(B - A)

②保证每次相减都是大的数 - 小的数

③示例

                

#include<iostream>
#include<vector>
#include<string>
#include<algorithm>

using namespace std;

vector<int> sub(vector<int>& A,vector<int>& B)
{
    int t = 0; //借位标志
    vector<int> res;
    
    for(int i = 0 ; i < A.size() ; ++i)
    {   
        t = A[i]-t;
        if(i < B.size())  t -= B[i];
        
        res.push_back((t+10)%10); // t > 0 , (t + 10)%10 = t
        
        if(t < 0) t = 1;
        else t = 0;
    }
    
    //去除后缀0
    while(res.size() > 1 && res.back() == 0)  
    res.pop_back();
    
    return res;
    
}

bool cmp(vector<int>& A,vector<int>& B)
{
    //都是小细节 
    if(A.size() != B.size())
    {
       return A.size() > B.size();
    }
    
    for(int i = A.size()-1 ; i >=0 ; --i) // == 
    {
        if(A[i] != B[i])
        {
            return A[i] > B[i];
        }
    }
    
    // A,B所有元素相等
    return true;
}


int main()
{
    vector<int> A;
    vector<int> B;
    
    string str1;
    string str2;
    cin>>str1>>str2;
    
    
    //逆序插入数组
    for(int i = str1.size()-1 ; i >=0 ;--i)
    {
        A.push_back(str1[i]-'0');
    }
    
    for(int i = str2.size()-1 ; i >=0 ;--i)
    {
        B.push_back(str2[i]-'0');
    }
    
    
    vector<int> ret;
    if(cmp(A,B) == true)
    {
       ret = sub(A,B);
    }
    else
    {
        cout << "-";
        ret = sub(B,A);
    }
    
   
    for(int i = ret.size()-1 ; i >= 0;--i)
    {
        cout << ret[i];
    }
    

    return 0;
}

                        

                 

 3.高精度乘法

①将较小的数看做一个整体去和大的数的每一位相乘

②取模( %10 )做结果 , 取除( /10 )做进位

③示例 : A  = 0 - 999999

                 

#include<iostream>
#include<vector>
#include<string>

using namespace std;

vector<int> mul(vector<int>& A,const int b)
{
    int Carry = 0; //进位标志
    vector<int> res;
    
    for(int i = 0 ; i < A.size() ; ++i)
    {   
        Carry += A[i] * b;
        res.push_back( Carry % 10);
        Carry /=  10;
    }
    
    //直接将Carry push进去
    if(Carry != 0) res.push_back(Carry);
    
    /*
    for(int i = 0 ; i < A.size() || Carry  ; ++i)
    {   
        if(i < A.size()) Carry += A[i] * b;
        res.push_back( Carry % 10);
        Carry /=  10;
    }
    */
    
    while(res.size() > 1 && res.back() == 0)
    res.pop_back();
    
    
    return res;
    
}


int main()
{
    vector<int> A;
    int b;
    
    string str1;
    cin>>str1>>b;
    
    
    //逆序插入数组
    for(int i = str1.size()-1 ; i >=0 ;--i)
    {
        A.push_back(str1[i]-'0');
    }
    
    auto C = mul(A,b);
    for(int i = C.size()-1 ; i >= 0;--i)
    {
        cout << C[i];
    }
    

    return 0;
}

                

                 

4.高精度除法

• 注意去除前面多余的0 和 商为0 的情况

                 

                         

#include<iostream>
#include<vector>
#include<string>

using namespace std;

vector<int> div(vector<int>& A,const int b, int& rem)
{
    vector<int> res;
    
    for(int i = 0 ; i < A.size() ; ++i)
    {   
        rem = rem*10+A[i];
        res.push_back(rem / b);
        rem %= b;
    }
    
    return res;
    
}


int main()
{
    vector<int> A;
    int b;
    
    string str1;
    cin>>str1>>b;
    
    //逆序插入数组
    for(int i = 0 ; i < str1.size() ;++i)
    {
        A.push_back(str1[i]-'0');
    }
    
    int rem = 0; //余数，带回来
    auto C = div(A,b,rem);
    
    
    //去除前面多余0
    int i = 0;
    while(i < C.size() && C[i] == 0 ) ++i;
    if(i == C.size())
    {
        cout << 0 << endl;
        cout << rem << endl;
        
        return 0;
    }
    
    for(; i < C.size();++i)
    {
        cout << C[i];
    }
    cout << endl;
    cout << rem;
    
    

    return 0;
}