二分法精讲-优快云博客

1.整数二分

①有单调性一定可以进行二分，没有单调性的题目也可以进行二分，二分的本质不是单调性

②二分的本质是寻找性质的边界

只要我们的区间可以找到这样一个性质，就可以用二分把边界点二分出来
边界可以是灰色点，也可以是绿色点；灰色点和绿色点就是两个不同的模板

③ 两个不同的模板

补充: ①中为什么要+1，
当left = right-1时， mid = (left+right) /2 向下取整 mid = left ，再使left = mid时和原来一样，就陷入了死循环
如果+1 ，即 mid = (left+right+1) / 2 = right 再使left = mid时就结束循环了

④模板代码

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

⑤在一个区间内，我们每次都要选择答案所在那个区间进行处理；每次我们把整个区间的长度缩小一半,选择一个答案所在的区间，每次都能保证区间里面是有答案的。

⑥在一个区间内部去二分一下边界，每次在选择答案所在的区间的时候，每次都能保证区间是一定有答案的，题目可能无解，二分一定有解

(1)题目示例

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
       vector<int> res;
       
       int n = nums.size();
       if(n < 1)
       {
           res.push_back(-1);
           res.push_back(-1);
           return res;
       }

       int left = 0; 
       int right = n-1;

       //找到开始位置
       while(left < right)
       {
           int mid = left + right >> 1;
           if(nums[mid] >= target)  right = mid;
           else  left = mid+1;
       }

       //有数据left，right就重合了
       if(nums[left] != target)
       {
          res.push_back(-1);
          res.push_back(-1);
       }
       else
       {
          res.push_back(left);

          left = 0 ;
          right = n-1;
          //找到结束的位置
          while(left < right)
          {
              int mid = left+right+1 >> 1;
              if(nums[mid] <= target) left = mid;
              else  right = mid-1;
          }

          res.push_back(left);
       }

       return res;
    }
};

(2)题目示例2

求某个数平方根，只要求输出其正数平方根，如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。
一个数的平方根肯定不会超过它自己，不过直觉还告诉我们，一个数的平方根最多不会超过它的一半，例如 8 的平方根，8 的一半是 4， 4^2= 16 > 8，如果这个数越大越是如此，因此我们要计算一下，这个边界是多少。为此，解如下不等式：(a/2) ^ 2 >= a

 int mySqrt(int x) 
    {
       if(x == 0)
       {
           return 0;
       }

       long left =  1;
       long right = x; // x/2

       while(left < right)
       {
           long mid = (left + right+1) >> 1;
           long square = mid*mid;
           if(square <= x)
           {
              left = mid;
           }
           else
           {
              right = mid-1;
           }
       }

       return (int)left;
    }

(3)题目示例3

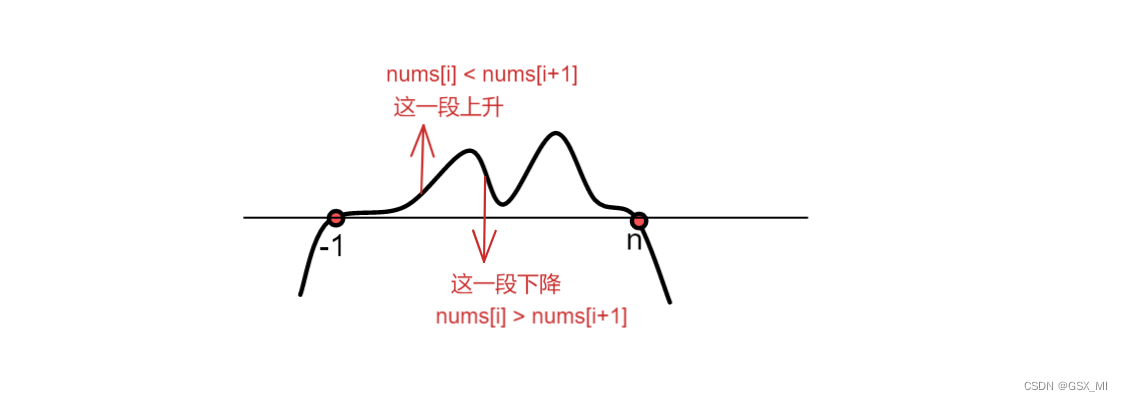
这道题最最最重要的是条件，条件，条件，两边都是负无穷，数组当中可能有很多波峰，也可能只有一个，这道题还有只是返回一个波峰。你这样想，中点所在地方，可能是某座山的山峰，山的下坡处，山的上坡处，如果是山峰，最后会二分终止也会找到，关键是我们的二分方向，并不知道山峰在我们左边还是右边，送你两个字你就明白了，爬山（没错，就是带你去爬山），如果你往下坡方向走，也许可能遇到新的山峰，但是也许是一个一直下降的坡，最后到边界。但是如果你往上坡方向走，就算最后一直上的边界，由于最边界是负无穷，所以就一定能找到山峰。
总的一句话，往递增的方向上，二分，一定能找到，往递减的方向只是可能找到，也许没有

class Solution {
public:
    int findPeakElement(vector<int>& nums) 
    {
       int left = 0;
       int right = nums.size()-1;

       while(left < right)
       {
           int mid = left + right >> 1;
           if(nums[mid] > nums[mid+1])
           {
               right = mid;
           }
           else
           {
               left = mid+1;
           }
       }

       return left;
    }
};

2.浮点数二分

①代码模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

②题目示例

求某个数的平方根，不能使用函数

int main()
{
	double d ;
	cin >> d;

	double left = 0, right = d;
	while (right - left > 1e-8) //计算结果保留小数的位数
	{
		double mid = (left + right) / 2;
		if (mid * mid >= d)
		{
			right = mid;
		}
		else
		{
			left = mid;
		}
	}
	printf("%lf\n", left);
	return 0;
}