样本数据相关性matlab

1、相关系数公式

---

相关系数的绝对值越大，表示随机变量之间的 关联越强。

2、matlab函数

---

2.1 corrcoef

---

R = corrcoef(x,y)

corrcoef（x，y）表示序列x和序列y的相关系数，得到的结果是一个2*2矩阵，其中对角线上的元素分别表示x和y的自相关，非对角线上的元素分别表示x与y的相关系数和y与x的相关系数，两个是相等的。

数据：

1 1.2
2 1.9
3 3.1
4 4
5 5.6
6 6.2
7 6.8

代码：

data = load('data1.txt');
x = data(:,1);
y = data(:,2);
R = corrcoef(x, y)

可以看到，自相关系数为1，因为自身与自身完全一样，x与y的相关系数为0.9927，非常接近1，表示两序列有很强的正相关性。

2.2 其他处理数据的函数

---

2.2.1 MIN、MAX、MEAN、MEDIAN 函数

MIN = min(data);  % 每一列的最小值
MAX = max(Test);   % 每一列的最大值

MEAN = mean(data);  % 每一列的均值MEDIAN = median(Test);  %每一列的中位数
MEDIAN = median(data)%每一列的中位数

2.2.2 SKEWNESS、KURTOSIS函数

偏度（skewness）也称为偏态、偏态系数，是统计数据 分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。

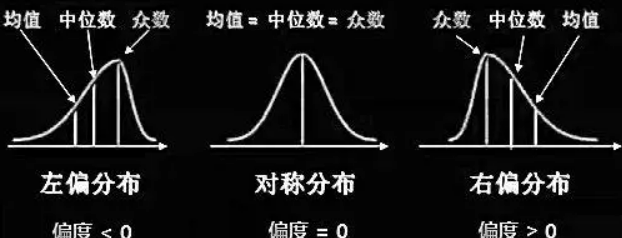
• 正态分布：偏度 = 0，两侧尾部长度对称。

• 右偏分布（正偏分布）：偏度 > 0，右侧（正方向）尾部较长。

• 左偏分布（负偏分布）：偏度 < 0，左侧（负方向）尾部较长。

正态分布：众数 = 中位数 = 均值

右偏：众数 < 中位数 < 均值

左偏：均值 < 中位数 < 众数

峰度（peakedness;kurtosis）又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言，如果峰度大于3，峰的形状比较尖，比正态分布峰要陡峭。

• 正态分布： 峰度 = 3。

• 厚尾分布：峰度 > 3。

• 瘦尾分布：峰度 < 3。

SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test);  %每一列的峰度

2.2.3 STD函数

标准差（Standard Deviation），在概率统计中最常使用作为统计分布程度（statistical dispersion）上的测量。标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。测量到分布程度的结果，原则上具有两种性质：

1. 为非负数值，与测量资料具有相同单位。一个总量的标准差或一个随机变量的标准差，及一个子集合样品数的标准差之间，有所差别。

2. 简单来说，标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。

STD = std(Test);  % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]  %将这些统计量放到一个矩阵中表示

2.2.4 var函数

函数var可以用来计算方差

V = var(X)   % 样本方差，分母除的是n-1(当n>1时)，当n=1时，除n
V = var(X,1) % 二阶矩，也就是总体方差，分母除的是n

3、相关系数完整计算代码

data = load('data1.txt');
x  = data(:,1);
y  = data(:,2);
R0 = corrcoef(x, y) % 相关系数
% 以下是测试
mu_x  = mean(x); % x均值
mu_y  = mean(y); % y均值
diffx = x - mu_x; % 行列与x一样
diffy = y - mu_y;
covxy = sum(diffx.*diffy)/(size(diffx,1)-1); % x与y的协方差，用的n-1
sigx  = sqrt(var(x,0)); % 标准差，用的n-1
sigy  = sqrt(var(y,0));
R     = covxy/(sigx*sigy)

参考资料：

matlab中样本相关系数的计算与测试itsc的博客-优快云博客matlab 样本相关系数

spss-偏度和峰度 - 简书 (jianshu.com)