时间复杂度问题

时间频度

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

时间复杂度

前面提到的时间频度T(n)中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律，为此我们引入时间复杂度的概念。一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T（n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(f(n))，它称为算法的渐进时间复杂度，简称时间复杂度。

时间复杂度-->时间频度

算法执行时间∝算法执行次数

时间复杂度大小关系大致：o(1)<o(logn)<o(n)<o(nlogn)<o(n^2)<o(n^3)<...

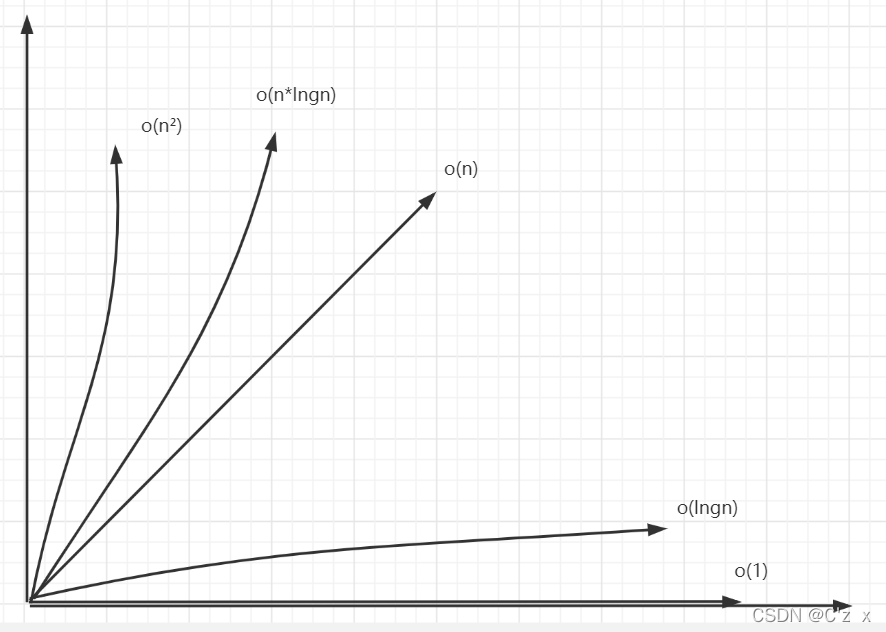
怎么判断程序的时间复杂度

• 快速的判断时间复杂度
  • 确定问题规模n
  • 循环减半过程
  • k层关于n的循环--->n^k
• 复杂情况：根据算法执行过程判断

O(1)

int n = 1;
System.out.println(n);
int m = 1;
System.out.println(m);
System.out.println(m+1)
System.out.println(m+2)

O(log(n))

for (int i = 0; i < n; i = i * 2) {
    count++;//这里是以2为底n的对数
}

O(n)

for (int j = 0; j < n; j++) {
    count++;
}

O(n*2)

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
         count++;
    }
}

O(nlog(n))

int count = 0;
for(int i = 1;i<n;i++){
    for(int j=1;j<=2*i;j++){
         count++;
    }
}

 如果直接看不能看出规律可以带入几个值看执行次数，画图看和四种图像那个相似，就是那种时间复杂度

时间复杂度例题讲解

void fun(int n){
    int i=0;s=0;
    while(s<n){
        ++i;
        s = s +i;  
    }
}

基本算法：s=s+i；

第一次执行：s=1

第二次执行：s=3

第三次执行：s=6

第四次执行：s=10

第五次执行：s=15

...

第t次执行：s=t(t+1)/2

s<n

t^2<n，即t<n^1/2

时间复杂度为o(n^1/2）

int func(int n){
    if(n<=1)
    	return 1;
     else
          return n*func(n-1)
}

基本算法：执行次数=n；

第一次执行：执行1次；

第二次执行：执行2次；

第三次执行：执行3次；

第四次执行：执行4次；

第五次执行：执行5次；

t=n

时间复杂度为o(n)

void func(int n){
    i = 1;
    while(i<n){
        i  = i*3;    
    }
}

基本算法：i  = i*3；

第一次执行：i=3；

第二次执行：i=9；

第三次执行：i=27；

第t次执行：i=3^t

3^t<n  t<log3(n)   

时间复杂度o(log3n)

for(int i=1;i<=n;i++){
    for(int  j =1;j<=i;j++){
        for(int  k =1;k<=j;k++){
            count ++;    
        }
    }
}

n=1;执行1次

n=2;执行8次

n=3;执行27次

n=t;执行t^3

时间复杂度为o(n^3)

for(int i=1;i<=n;i*=2){
	count ++;
}

n=1;count执行1次;

n=2;count执行4次;

n=3;count执行8次;

n=t;count执行2^t次;

2^t<n  t<log2n

时间复杂度o(logn)

int func(int n){
	int i =0 ,sum = 0;
	while(sum < n){
	  sum += ++i;
	}
	return i;
}

n=1;sum=1

n=2;sum=1+2

n=3;sum=1+2+3

n=4;sum=1+2+3+4

n=t;sum=1+2+3+...+t（为一的等差数列）

sum<n

t+t(t-1)/2<n

t<n^1/2

时间复杂度为o(n^1/2)

void fun(int n){
    int i = 0;
    while(i*i*i <= n){
        i++;    
    }
}

n=1;0*0*0

n=2;1*1*1

n=3;2*2*2

n=t;(t-1)*(t-1)*(t-1)

(t-1)^3<=n

t<n^1/3

时间复杂度为o(n^1/3)

x = 0;
while(n>=(x+1)*(x+1)){
    x = x + 1;
}

n=1;1*1

n=2;2*2

n=3;3*3

n=t;t*t

t^2<=n

t<n^1/2

时间复杂度为o(n^1/2)

for(i=0;i<n;i++){
    for(j =0;j<m;j++){
         a[i][j] = 0;
    }
}

第一层for循环执行n次，第二层for循环执行m次

时间复杂度为o(n*m)

int m = 0,i,j;
for(i = 1;i<n;i++){
    for(j=1;j<=2*i;j++){
         m++;
    }
}

第一层for循环执行n次，第二层for循环执行logn次

时间复杂度为o(nlogn)

int count=0;
for(int i=1;i<=n;i*=2){
    for(int j=1;j<=i;j++){
        count++;    
    }
}

i=1  执行1次

i=2  执行3次

i=4  执行7次

i=8  执行15次

i=16  执行31次

i=32  执行63次

 时间复杂度为o(n)

八大排序的时间复杂度：

冒泡排序：O（n^2）

简单选择排序：O（n^2）

插入排序：O（n^2）

希尔排序：O(nlogn)

堆排序：O(nlogn)

基数排序：O(kn)

归并排序：O(nlogn)

递归排序：O(nlogn)