Flow-based Generative Model
文章为看视频Flow-Based Model-李宏毅的笔记
1.生成模型的分类
- Auto-regressive Model(Component-by-component)
- Variational Auto-encoder:优化的是一个下界
- Generative Adversarial Network
- Flow-based Model:
2.Flow-based Generative Model的数学原理
2.1Jacobian
x = f ( z ) x = f(z) x=f(z)
针对上述函数
f
f
f,它的Jacobian是x的各项对z的各项求偏微分后组合得到的矩阵

针对函数
f
f
f 和
f
−
1
f^{-1}
f−1:
x
=
f
(
z
)
x = f(z)
x=f(z)
z = f − 1 ( x ) z = f^{-1}(x) z=f−1(x)
f
f
f 和
f
−
1
f^{-1}
f−1 是inverse function,那么它们的Jacobian也是inverse的,即相乘得到
I
I
I(单位矩阵):
J
f
J
f
−
1
=
I
J_f J_{f{-1}}=I
JfJf−1=I
2.2Determinant
意义:将一个矩阵算出一个scalar,代表高维空间的体积
2.3Change of Variable Theorem
针对变化:
x
=
f
(
z
)
x = f(z)
x=f(z)
general的变量变化公式如下:
p
(
x
)
∣
d
e
t
(
J
f
)
∣
=
π
(
z
)
p(x)|det(J_f)| = \pi(z)
p(x)∣det(Jf)∣=π(z)
即:
p
(
x
)
=
π
(
z
)
∣
1
/
d
e
t
(
J
f
)
∣
=
π
(
z
)
∣
d
e
t
(
J
f
−
1
)
∣
p(x) = \pi(z) |1/det(J_f)| = \pi(z) |det(J_{f{-1}})|
p(x)=π(z)∣1/det(Jf)∣=π(z)∣det(Jf−1)∣
最终用的是:
p
(
x
)
=
π
(
z
)
∣
d
e
t
(
J
f
−
1
)
∣
p(x) = \pi(z) |det(J_{f{-1}})|
p(x)=π(z)∣det(Jf−1)∣
2.4Flow-based Model原理
Generator:
x
=
G
(
z
)
x = G(z)
x=G(z)
G
e
n
e
r
a
t
o
r
−
1
Generator^{-1}
Generator−1:
z
=
G
−
1
(
x
)
z = G^{-1}(x)
z=G−1(x)
根据变量变化公式:
p
G
(
x
)
=
π
(
z
)
∣
d
e
t
(
J
G
−
1
)
∣
p_G(x) = \pi(z)|det(J_{G^{-1}})|
pG(x)=π(z)∣det(JG−1)∣
取log(并将
z
=
G
−
1
(
x
)
z = G^{-1}(x)
z=G−1(x)代入得到):
l
o
g
p
G
(
x
)
=
l
o
g
π
(
G
−
1
(
x
)
)
+
l
o
g
∣
d
e
t
(
J
G
−
1
)
∣
logp_G(x) = log\pi(G^{-1}(x)) + log|det(J_{G^{-1}})|
logpG(x)=logπ(G−1(x))+log∣det(JG−1)∣
Flow-based Model要求:
G
∗
=
arg
max
G
∑
i
=
1
m
log
p
G
(
x
i
)
G^* = \arg\max_G \sum_{i=1}^{m} \log p_G(x^i)
G∗=argGmaxi=1∑mlogpG(xi)
其中
x
i
x^i
xi代表从真实分布
p
D
a
t
a
p_{Data}
pData采样得到的真实样本
再具体一些,我们得到的z满足均值为0,方差为1的多变量高斯分布,即z ~ $ N(0, I)$,即
p
Z
(
z
)
=
(
2
π
)
−
d
2
e
−
1
2
z
T
z
p_Z(z) = (2\pi)^{-\frac{d}{2}} e^{-\frac{1}{2} z^T z}
pZ(z)=(2π)−2de−21zTz
因此,计算x的Log-likelihood可以按照下述公式:
l
o
g
p
G
(
x
)
=
−
d
2
log
(
2
π
)
−
1
2
G
−
1
(
x
)
T
G
−
1
(
x
)
+
∑
l
=
1
L
log
∣
det
J
G
l
−
1
(
y
l
−
1
)
∣
logp_G(x) = -\frac{d}{2} \log(2\pi) - \frac{1}{2} G^{-1}(x)^T G^{-1}(x) + \sum_{l=1}^L \log \left| \det J_{G^{-1}_l}(y_{l-1}) \right|
logpG(x)=−2dlog(2π)−21G−1(x)TG−1(x)+l=1∑Llog
detJGl−1(yl−1)
其中,
y
0
=
x
∈
X
y_0 = x ∈ X
y0=x∈X,
y
L
=
z
∈
Z
y_L = z ∈Z
yL=z∈Z,
y
l
=
G
l
−
1
(
y
l
−
1
)
y_l = G^{-1}_l(y_{l-1})
yl=Gl−1(yl−1),其中
{
y
l
}
l
=
1
L
−
1
\{y_l\}^{L-1}_{l=1}
{yl}l=1L−1是
G
−
1
G^{-1}
G−1的中间输出。
其中,
z
=
G
−
1
(
x
)
z = G^{-1}(x)
z=G−1(x),公式也可以写成:
l
o
g
p
G
(
x
)
=
−
d
2
log
(
2
π
)
−
1
2
z
T
z
+
∑
l
=
1
L
log
∣
det
J
G
l
−
1
(
y
l
−
1
)
∣
logp_G(x) = -\frac{d}{2} \log(2\pi) - \frac{1}{2} z^Tz + \sum_{l=1}^L \log \left| \det J_{G^{-1}_l}(y_{l-1}) \right|
logpG(x)=−2dlog(2π)−21zTz+l=1∑Llog
detJGl−1(yl−1)
要确保G可逆,z和x的dimension是一样的(G可逆的必要不充分条件)
2.5多个G串联
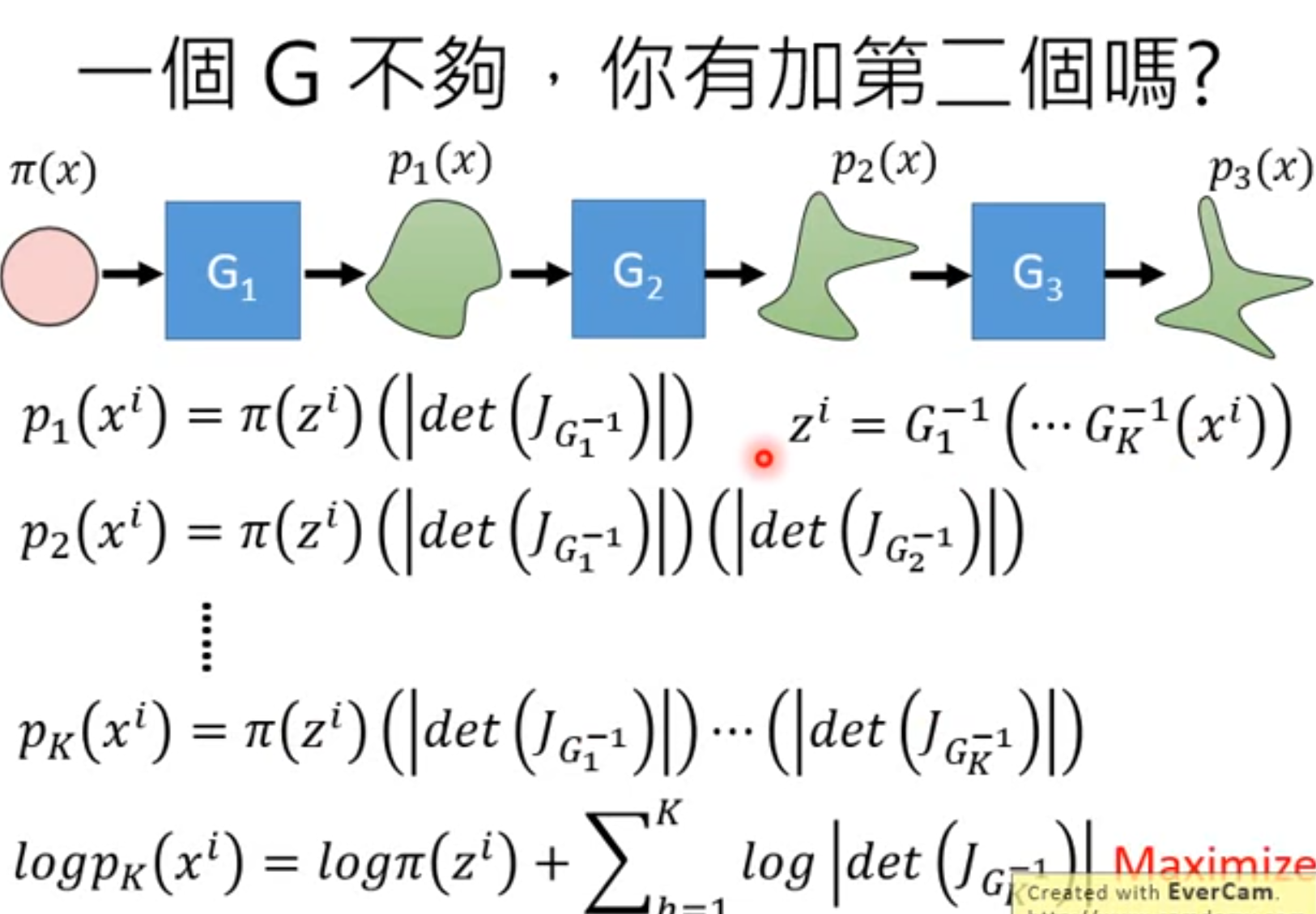
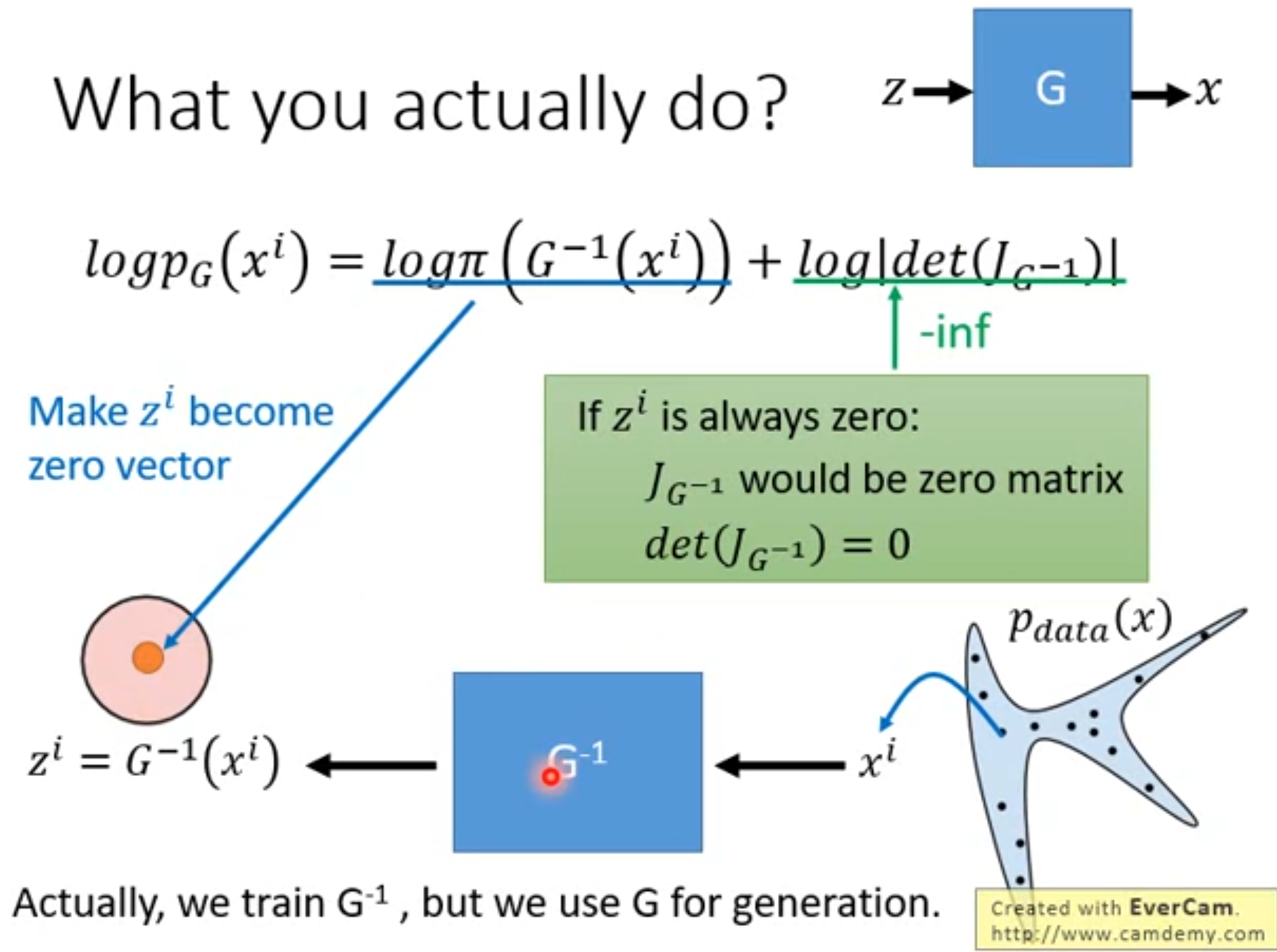
2.6实际怎么训练
根据公式:
l
o
g
p
G
(
x
)
=
l
o
g
π
(
G
−
1
(
x
)
)
+
l
o
g
∣
d
e
t
(
J
G
−
1
)
∣
logp_G(x) = log\pi(G^{-1}(x)) + log|det(J_{G^{-1}})|
logpG(x)=logπ(G−1(x))+log∣det(JG−1)∣
我们要最大化
p
G
(
x
)
p_G(x)
pG(x),得到
G
∗
G^*
G∗:
G
∗
=
arg
max
G
∑
i
=
1
m
log
p
G
(
x
i
)
G^* = \arg\max_G \sum_{i=1}^{m} \log p_G(x^i)
G∗=argGmaxi=1∑mlogpG(xi)
其实只涉及到
G
−
1
G^{-1}
G−1,所以我们实际是训练
G
−
1
G^{-1}
G−1(
z
=
G
−
1
(
x
)
z = G^{-1}(x)
z=G−1(x)),
G
−
1
G^{-1}
G−1训练好之后,再把它反过来得到
G
G
G,去完成生成任务(
x
=
G
(
z
)
x = G(z)
x=G(z))
2.7Coupling Layer 和 C o u p l i n g L a y e r − 1 Coupling\ Layer^{-1} Coupling Layer−1
Coupling Layer 和 C o u p l i n g L a y e r − 1 Coupling\ Layer^{-1} Coupling Layer−1相当于G和 G − 1 G^{-1} G−1
Coupling Layer相当于多个G串联时候的每一个G,是生成器Generator
Generator:由z算x(即:怎么算Coupling Layer)
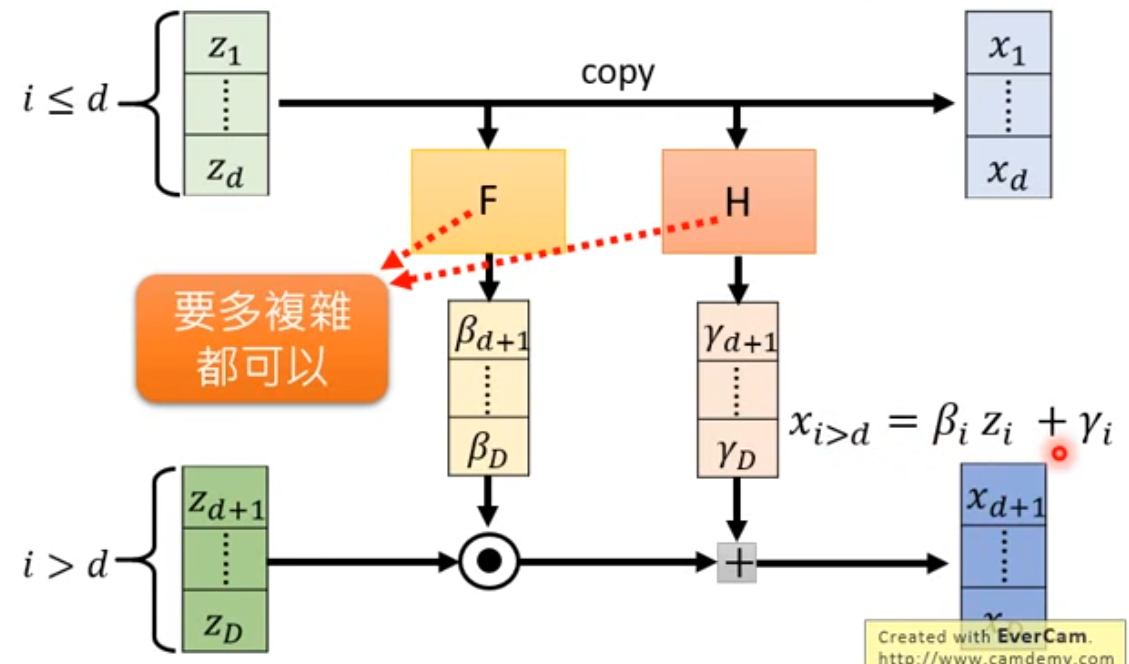
C o u p l i n g L a y e r − 1 Coupling\ Layer^{-1} Coupling Layer−1相当于多个 G − 1 G^{-1} G−1串联时候的每一个 G − 1 G^{-1} G−1
C
o
u
p
l
i
n
g
L
a
y
e
r
−
1
Coupling\ Layer^{-1}
Coupling Layer−1:由x算z(即:怎么算Coupling Layer的inverse,代表
G
−
1
G^{-1}
G−1)
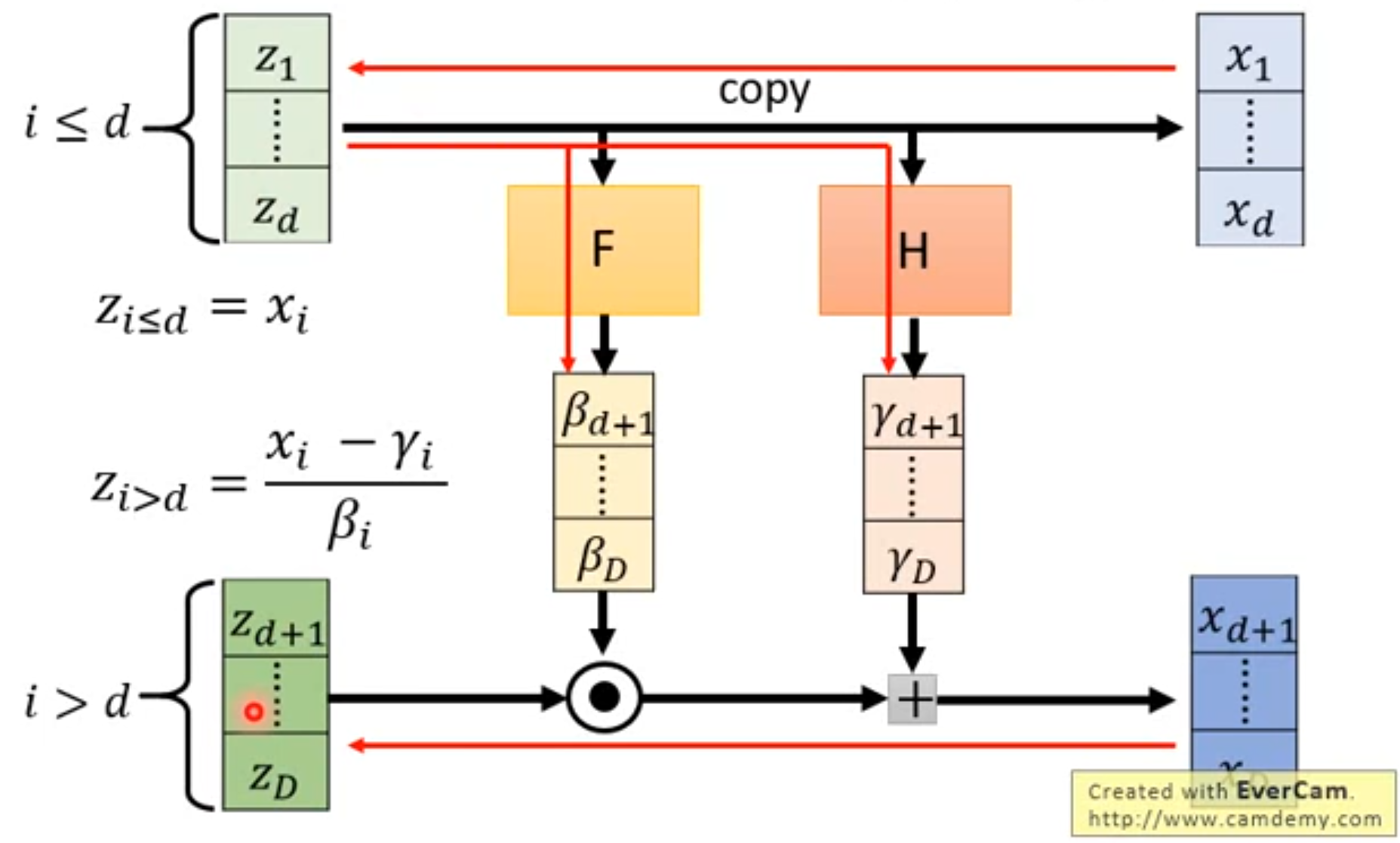
2.8怎么算Coupling Layer的Jacobian
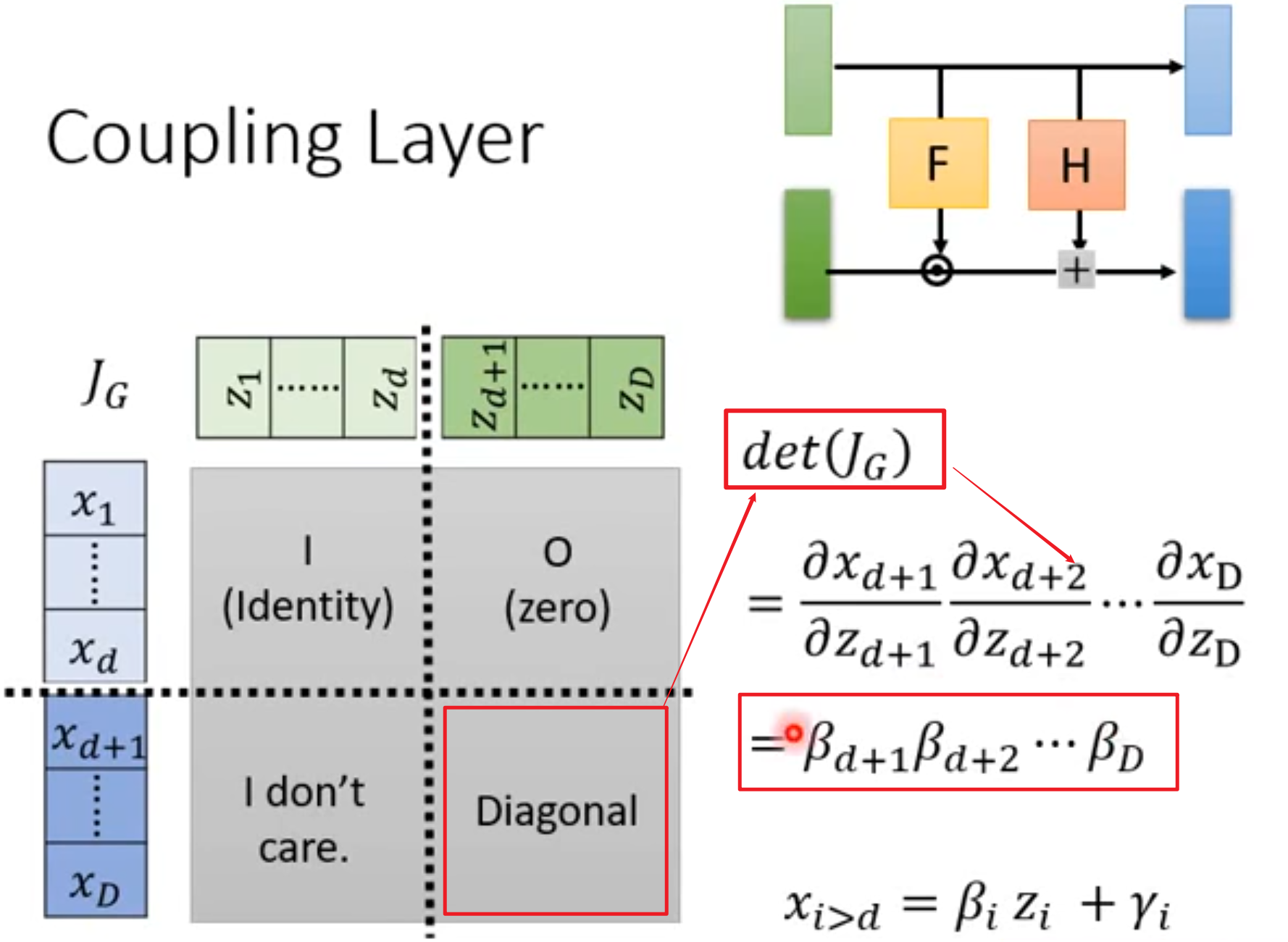
2.9堆叠Coupling Layer
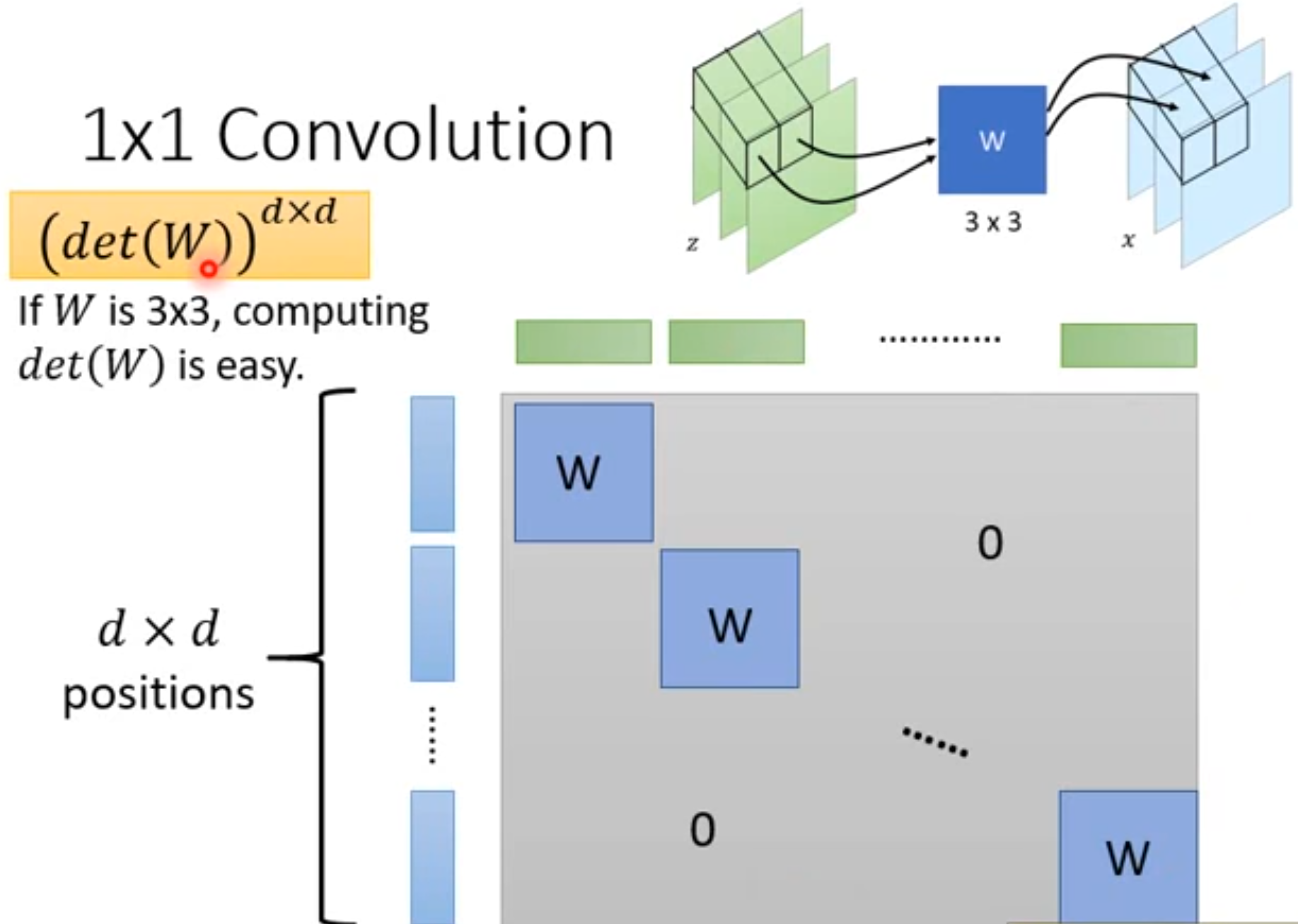
直接堆Coupling Layer会导致不变的高斯噪声部分会延续到最终结果中,所以不是直接堆叠。GLOW中利用1x1Convolution来交换channel,然后coupling layer就可以每次保留固定index的channel的信息,最终起到每次保留不同channel的信息,从而不会把高斯噪声带到最后。这里的1x1Convolution也是生成器的一部分,所以也需要是可逆的,它的Jacobian见右下角,(只有对角线为3x3的W矩阵,其余为0,因为只有对着的绿色蓝色部分是互相有影响的,求偏微分有值,其余没有相对着的互相无影响,求偏微分为0),这个Jacobian的det值见左上橙色部分,为
d
e
t
(
W
)
d
∗
d
det(W)^{d*d}
det(W)d∗d

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








