GCN半监督分类
一、傅里叶变换和卷积
1.图的卷积
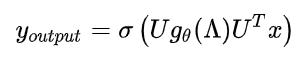
- X为图的节点的特征提取构成的向量(相当于是图的一个节点信息的输入)
- U 为拉普拉斯矩阵的特征向量矩阵
- gθ 为卷积核
由于上述公式当中激活函数、U和x均为已确定的变量,故对卷积核gθ作改进。
2.第一代GCN
第一代GCN将gθ按如下定义:
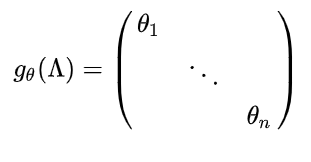
其中的θ有n个(也就是和图的节点数相同),是通过初始化赋值,然后进行误差的反向传播进行调整。
【误差反向传播】:
- 过程:
输出误差(某种形式)->隐层(逐层)->输入层
- 主要目的:
通过将输出误差反传,将误差分摊给各层所有单元,从而获得各层单元的误差信号,进而修正各单元的权值
- 实质
是一个权值调整的过程,也就是网络的学习训练过程。
缺点:在大规模的图中,n值会相当大,整个公式的计算量会很大,因此提出第二代GCN。
3.第二代GCN
第二代GCN将gθ按如下定义:
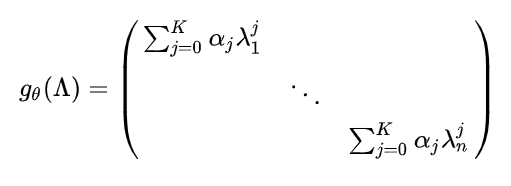
其中的α同初代GCN中的θ一样是通过初始化赋值,然后进行误差的反向传播进行调整,K表示从图中的任意一个中心节点到到任意一阶的步数,可以得到,K远小于n。
从以上公式来看,卷积核公式仿佛比初代GCN更加复杂,但是把它带入到GCN的卷积公式中,化简为:
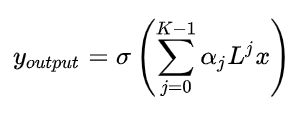
优点:
- 可以看出,该算式只需要K次求和操作即可
- 矩阵变换后不需要特征分解了,直接用拉普拉斯矩阵L变换
- 每次卷积会将中心顶点k-hop neighbor上的feature进行加权求和,权系数是 α k \alpha{k} αk,k=1即对每个顶点上一阶邻居的feature进行加权求和
4.第三代GCN
第三代GCN将gθ用切比雪夫Chebyshev多项式T k ( x )到Kth的截断展开来近似:
Chebyshev多项式:
Tk(x)=2xTk-1(x)-Tk-2(x)
T0(x)=1
T1(x)=x
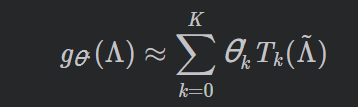
Λ ^ \hat\Lambda Λ^是特征值对角矩阵(为什么要进行这个shift变换?chebyshev多项式的输入要在[-1,1]之间,怎么做呢?除以 λ m a x \lambda_{max} λmax就转化在了[0,1]区间,再进行2*[0,1]-1,即可)
可以看到,该公式与第二代GCN用到的卷积公式非常相似,最终都将参数简化到了K 个,并不再需要做特征分解,直接用拉普拉斯矩阵L 进行变换,计算复杂性大大降低。
但本文使用了切比雪夫多项式Tk(x) ,这是与第二代GCN中的卷积公式的不同点。
二、作者的改进
由上述可得,基于图的卷积公式为:
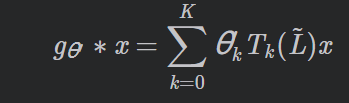
接着上述的工作,作者提出了层状线性模型
1.两个参数的模型
作者将每层的卷积操作限制为K=1,即关于L 是线性的,因此在拉普拉斯谱上有线性函数,借助这种线性运算方式,作者仍然可以通过堆叠多个这样的卷积层运算来恢复卷积滤波函数的表达能力。进一步近似使得 λ m a x \lambda{max} λmax≈2,则将上述公式化简为:
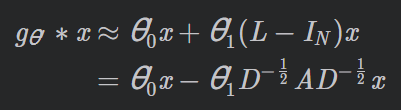
(为什么要使
λ
m
a
x
\lambda_{max}
λmax≈2?这样对于中心节点进行一层卷积时,只利用了距离中心节点最近的邻居节点,那么对第一层卷积结果进行重复这样的卷积可以扩展到第二层邻居节点,跟以前不同的是,不一次性进行k order,而是通过1 order的累加k次获得k order的结果)
- 此公式具有两个自由参数: θ 0 \theta{0} θ0 和 θ 1 \theta{1} θ1,滤波器参数将被整个图共享
- 连续应用这种形式的滤波器,可以有效的卷积节点的 k t h k^{th} kth-阶邻域,其中k 是模型中连续滤波操作或卷积层的数目。
2.简化:一个参数的模型
由于是卷积神经网络,滤波器参数对整幅图操作时遵循权值共享原则,连续地运用这种滤波器操作能够高效地卷积各个节点的第k层卷积层相邻区域。通常来说,限制参数的数量可以进一步解决过拟合并将各层的运算量最小化,所以令θ =
θ
0
\theta_{0}
θ0 =
θ
1
\theta_{1}
θ1 ,将两个参数化为单参数θ ,得到卷积公式如下:
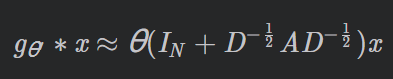
这里
I
N
I_{N}
IN+
D
−
1
/
2
D^{-1/2}
D−1/2
A
A
A
D
−
1
/
2
D^{-1/2}
D−1/2的特征值范围是[0,2],这将会导致数值不稳定性和梯度爆炸或者梯度消失。因此下面进行归一化:
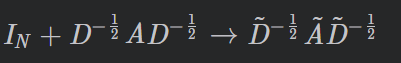
推广:特征映射公式
将该定义推广到具有C 个输入通道(即每个节点的C 维特征向量)的信号
X
N
×
C
X^{N×C}
XN×C和F 个滤波器,则特征映射(feature maps)如下:
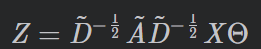
- Θ ∈ X C × F \Theta∈X^{C×F} Θ∈XC×F是滤波器参数矩阵
- Z ∈ X N × F Z∈X^{N×F} Z∈XN×F是卷积后的信号矩阵
三、总结
- 作者对于直接操作于图结构数据的网络模型根据频谱图卷积使用一阶近似简化计算的方法,提出了一种简单有效的层式传播方法
- 作者验证了图结构神经网络模型可用于快速可扩展式的处理图数据中节点半监督分类问题,作者通过在一些公有数据集上验证了自己的方法的效率和准确率能够媲美现有的顶级半监督方法
四、问题
1、设计第三代GCN的原因(第二代和第三代在实现效果上有何差别)
2、
θ
k
’
\theta^{’}_k
θk’的意义
3、为什么
λ
m
a
x
\lambda_{max}
λmax≈2
4、半监督学习




 博客围绕GCN半监督分类展开,先介绍傅里叶变换和卷积,包括图的卷积及三代GCN,指出初代GCN计算量大,后两代简化计算。接着阐述作者改进,提出层状线性模型,有两个参数和一个参数的模型。最后总结方法有效,还列出相关问题。
博客围绕GCN半监督分类展开,先介绍傅里叶变换和卷积,包括图的卷积及三代GCN,指出初代GCN计算量大,后两代简化计算。接着阐述作者改进,提出层状线性模型,有两个参数和一个参数的模型。最后总结方法有效,还列出相关问题。

















 821
821










