【GCN】论文笔记：Graph Attention Networks

---

一、前言

1、GAT概述

我们提出了图注意力网络(GATs)，这是一种基于图结构数据的新型神经网络体系结构，它利用隐藏的 self-attention layer 来解决基于图卷积或其近似的先前方法的缺点。通过叠加层，节点能够参与其邻居的特征，我们可以(隐式地)指定不同的权值到一个邻居的不同节点，而不需要任何类型的矩阵操作(如反演)或依赖于预先知道的图结构。
通过这种方式，我们同时解决了基于频谱的图神经网络的几个关键挑战，并使我们的模型适用于归纳和直推问题。我们的GAT模型在四个已建立的直推和归纳图基准上匹配的最新结果:Cora, Citeseer和Pubmed引文网络数据集，以及一个蛋白质蛋白质相互作用数据集(其中测试图在训练期间不可见)

1、GAT特点

针对每一个节点运算相应的隐藏信息，在运算其相邻节点的时候引入注意力机制：

• 高效：针对相邻的节点对，并且可以并行运算
• 灵活：针对有不同度（degree）的节点，可以运用任意大小的weight与之对应。
• 可移植：可以将模型应用于从未见过的图结构数据，不需要与训练集相同。

2、相关工作

• 谱方法：Semi-Supervised Classification with Graph Convolutional Networks
  在每个节点周围对卷积核做一阶邻接近似。但是此方法也有一些缺点：
  ----必须基于相应的图结构才能学到拉普拉斯矩阵L；
  ----对于一个图结构训练好的模型，不能运用于另一个图结构（所以此文称自己为半监督的方法）。
• 非谱方法：每个节点的相邻节点数量是不一样的，重点在于如何能设置相应的卷积尺寸来保证CNN能够对不同的相邻节点进行操作。
• 注意力机制 self-attention：可以处理任意大小输入的问题，并且关注最具有影响能力的输入。
  理解直推式和归纳式学习(https://blog.youkuaiyun.com/DreamHome_S/article/details/106165051)

二、方法推导

1、输入与输出

• 输入：一组节点特征，h={${\vec{h}}_1$,${\vec{h}}_2$,…,${\vec{h}}_N$,},${\vec{h}}_i$∈$R^F$
  其中 N 为节点数， F 为每个节点的特征数，即输入N个节点的每个节点的F个特征
• 输出：一组新的节点特征，h’={${\overrightarrow{h^{\prime }}}_1$,${\overrightarrow{h^{\prime }}}_2$,…,${\overrightarrow{h^{\prime }}}_N$,},${\overrightarrow{h^{\prime }}}_i$∈$R^{F^{\prime }}$

目的：针对这N个节点，按照其输入的特征预测输出的特征。

2、计算注意系数

对每一个节点应用权重矩阵,W∈$R^{F^{\prime }\times F}$, 接着我们在每一个节点上使用注意机制 a：$R^{F^{\prime }}$ × $R^{F’}$ →R

注意系数：$e_{ij}$=a(W${}^{{\vec{h}}_i}$,W${}^{{\vec{h}}_j}$)表示节点 j 的特征对节点 i 的重要性。
在这里，我们只计算$e_{ij}$，j∈$N_i$,实验表明，当$N_i$代表节点 i 的一阶邻居时效果最好。
为了使系数在不同节点之间易于比较，我们使用softmax函数对 j 的所有选择进行标准化:

在我们的实验中，注意机制a是一个单层前馈神经网络，被一个权重向量$\vec{a}$∈$R^{2F’}$参数化，并应用LeakyReLU非线性(负输入斜率α= 0.2)。完全展开后，注意机制计算出的系数可以表示为:

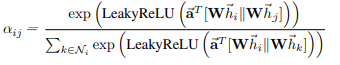
其中，||表示级联（拼接）操作。

3、加权求和

得到归一化的注意系数之后，就用它来计算其对应特征的线性组合，作为每个节点的最终输出特征：

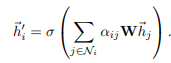
4、multi-head attention

为了稳定自我注意的学习过程，我们发现扩展我们的机制以使用multi-head是有益的。具体来说，将K个独立的注意机制进行如下变换，然后将它们的特征进行串级，得到如下输出特征表示:

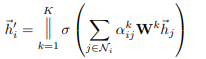
其中，${\alpha }_{ij}^k$表示第k个注意机制计算的归一化注意系数，W为对应的输入的线性变换的权重矩阵，注意，返回的输出${\overrightarrow{h^{\prime }}}_i$中每个节点将包含KF’个特征（超过F’）。
如果我们对网络的最终(预测)层进行multi-head关注，||就不再是明智的了,相反，我们使用平均，并延迟应用最终的非线性(通常是softmax或logistic sigmoid用于分类问题)，直到:

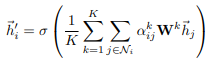
三、总结

1、GAT优点

• 在计算上是高效的，self-attentional layer的操作可以在所有边上并行化，输出特征的计算可以在所有节点上并行化,不需要特征分解或类似代价高昂的矩阵操作。采用multi-head注意机制将存储和参数要求乘以K，而各个头的计算完全独立，可以并行化。
• 与GCNs相反，我们的模型允许(隐式地)为同一邻居的节点分配不同的重要性，从而实现模型容量的飞跃。
• 注意机制以一种共享的方式应用于图中的所有边，因此它不依赖于对全局图结构或所有节点(特征)的预先访问(许多先前的技术的局限性)。这有几个可取的含义:
  – 图不需要是无向的(如果边j→i不存在，我们可以省去计算αij)。
  –这使得我们的技术直接适用于归纳学习——包括在训练过程中完全看不见的图形上评估模型的任务。

2、结论

我们提出了图注意网络(GATs)，一种基于图结构数据的新型卷积式神经网络，利用隐藏的自我注意层。图注意力层利用在这些网络是计算有效(不需要昂贵的矩阵运算,可平行的所有节点图中),在处理不同大小的邻域时允许不同重要性(隐式地)分配到不同的节点,和不依赖于知道整个图结构与先前的spectral-based upfront-thus解决许多理论问题的方法。我们利用注意力的模型在四个完善的节点分类基准(包括直推和归纳)中成功实现或匹配了最先进的性能(特别是使用完全看不见的用于测试的图表)。