【GCN】论文笔记：Simplifying Graph Convolutional Networks

---

一、前言

1、SGC研究背景

GCNs的灵感主要来自于深度学习方法，因此可能会继承不必要的复杂性和冗余计算。在本文中，我们通过去除连续层的非线性变换和折叠权重矩阵（反复去除GCN层之间的非线性变换并将结果函数分解为单一的线性变换）来减少这一超额复杂性。我们从理论上分析得到的线性模型，并表明它对应于一个固定低通滤波器，然后是一个线性分类器。值得注意的是，我们的实验评估表明，在许多下游应用中，这些简化不会对准确性产生负面影响。此外，产生的模型能够拓展到更大的数据集，且它的速度是惊人的，比FastGCN快两个数量级。我们将这个简化的线性模型称为简单图卷积(SGC)。

2、最终输入输出

• 输入：带有一些标签节点的图
• 输出：所有图节点的标签预测

（其实就是根据输入的已知的标签去预测图中未知的其余标签并尽量正确地分类）

3、符号定义

• 图G = ( V , A )，A ∈ $R^{n\times n}$ 是对称的邻接矩阵，V是图的节点集
• D = diag ⁡ ( d${}_1$ , … , d${}_n$ ) )代表度矩阵，d ${}_i$ = ${\sum }_j$ $a_{ij}$ ，
• $y_i$ ∈ { 0 , 1 }${}^C$ 表示C维的节点one-hot标签

二、GCN

跟CNN和MLP一样，GCN 也是通过多层网络学习一个节点的特征向量$X_i$，然后作为线性分类器的输入。对于一个k 层的图卷积网络，我们把输入表示成$H^{k-1}$，输出表示成$H^k$，那么初始输入特征表示为：$H^0$ $=$ $X$。一个k层的GCN相当于对图中每个节点的特征向量$x_i$应用一个k层的MLP，只不过每个节点的隐藏表示是在每一层的开始与它的邻居取平均值。在每一个图卷积层，节点表示都是使用三个策略来更新：特征传播、线性转换和逐点非线性激活。

1、特征传播

特征传播是区分GCN和MLP的关键。在每一层的开始，将每个节点$v_i$的特征$h_i$用其局部邻域的特征向量进行平均:

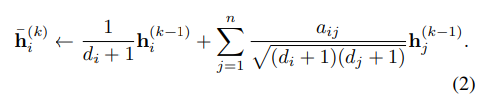
更简洁地说，我们可以将整个图的更新表示为一个简单的矩阵操作。设S表示加入自环的“归一化”邻接矩阵:

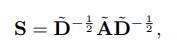
其中，$\tilde{A}$=$A$+$I$，$\tilde{D}$是$\tilde{A}$的度矩阵
则所有节点的同时更新成为一个简单的稀疏矩阵乘法：

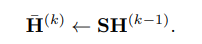
直观地说，这一步沿着图的边缘局部地平滑隐藏的表示，并最终鼓励在局部连接的节点之间进行类似的预测。
可以看出这一步的作用即为局部平滑

2、特征变换和非线性过渡

局部平滑后，GCN层与标准MLP相同。每一层都与一个学习过的权重矩阵${\Theta }^{(k)}$相关联，并对平滑过的隐藏特征表示进行线性变换。最后，在输出特征表示$H_k$之前，逐点应用ReLU等非线性激活函数。综上所述，第k层的表示更新规则为:

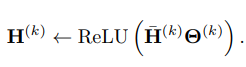
第k层的逐点非线性变换之后是第(k + 1)层的特征传播（由此得出每一层分别进行特征传播和非线性变换再进入到下一层）。

3、分类器

对于节点分类，类似于标准MLP, GCN的最后一层使用softmax分类器预测标签。

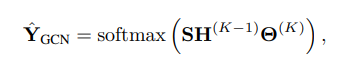
三、SGC

在传统的MLP中，更深的层增加了表达能力，因为它允许创建功能层次结构，例如，第二层的功能构建在第一层的功能之上。在GCNs中，各层还有第二个重要的功能:在每一层中，隐藏的表示在一跳之外的相邻层中取平均值。这意味着在k层之后，一个节点从图中k跳之外的所有节点获得特征信息。这种效果类似于卷积神经网络，深度增加内部特征的感受野。虽然卷积网络可以从深度的增加中获得很大的好处，但通常MLP在3或4层以上获得的好处很少。

1、线性化

假设：GCN层之间的非线性不是关键的，大部分的高效主要因为局部平均。
因此，我们删除了各层之间的非线性过渡函数，只保留最终的softmax(为了获得概率输出)。得到的模型是线性的，但仍然有k层GCN增加的“接受野”，

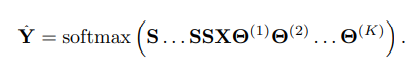
为了简化符号，我们可以把与标准化邻接矩阵S的重复乘法分解成一个单一的矩阵，取S的k次方，$S^k$。进一步，我们可以把我们的权值重新参数化为一个单一的矩阵θ=θ(1)θ(2)…${\Theta }^K$。产生的分类器变成:

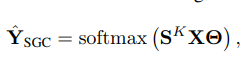
这就是SGC。

2、逻辑回归

由上一个公式可以看出，SGC由两部分组成：
(按顺序）

• 一个固定的特征提取器（平滑器）：$\bar{X}$=$S^K$X
• 线性逻辑回归分类器：$\tilde{Y}$=softmax($\bar{X}$$\Theta$)

由于$\bar{X}$的计算不需要权重，所以本质上相当于一个特征预处理步骤，整个模型的训练简化为对预处理后的特征$\bar{X}$进行直接的多类逻辑回归。

3、谱域分析

我们现在从图卷积的角度来研究SGC。我们证明了SGC对应于图谱域上的一个固定滤波器。此外，我们还证明了在原始图上添加自循环，即重正化技巧，可以有效地缩小底层图谱。在这个缩放域上，SGC充当低通滤波器，在图上产生平滑的特征。因此，邻近的节点倾向于共享相似的表示和预测。

四、总结

• 简化版的GCN，即SGC：移除连续层中的非线性变换，折叠权重矩阵减少计算复杂度，得到的线性模型等价于一个固定的低通滤波器。
• 实验结果证明证明去掉激活函数也可以在图学习任务上取得好的表现
• 带给我们的启示：GCNs的表达能力可能主要来自于重复的图传播（SGC保留了这一点），而不是非线性特征提取（SGC没有）。