光线追踪（ray tracing）实验报告+球体，长方体，折射，反射等+C++代码实现

这个世界是五彩斑斓，多姿多彩的。那么我们是怎么通过眼睛看到世界的呢？光线打到物体上再反射到我们的眼睛，不同物体由于其不同的材质对光的反射和吸收能力不同，从而使不同物体最终显现不同的颜色。本实验利用光线追踪绘制出一个具有球体，平面，光源的基本场景。

一.基本原理介绍

光线追踪方法主要思想是从视点向成像平面上的像素发射光线，找到与该光线相交的最近物体的交点，如果该点处的表面是散射面，则计算光源直接照射该点产生的颜色；如果该点处表面是镜面或折射面，则继续向反射或折射方向跟踪另一条光线，如此递归下去，直到光线逃逸出场景或达到设定的最大递归深度。
首先我们知道，物体在我们看来有颜色是因为光线打到物体上再将光线投射到我们的眼睛。那么反过来思考一下，如果顺着我们的眼睛视线方向前往物体表面，我们怎么知道此时这个表面是什么颜色呢？如果我们眼睛的视线方向能够与物体表面形成一个交点，那么此时我们眼睛看到的颜色便是这个物体的颜色。

二.代码介绍

1.vec3结构体

在geometry头文件里面，,vec3结构体里面包含x,y,z三个float变量，并且重载了+，-,*。定义了归一化函数，cross函数。该变量后期主要用表示三维空间里的点，方向，颜色三通道值等信息。

2.球体

struct Sphere
{
vec3 center;//球心
float radius;//球的半径
Material material;
Sphere(const vec3 &c, const float &r, const Material &m) : center(c), radius(r), material(m) {}
//判断射线和这个球是否相交，相交返回true
bool ray_intersect(const vec3 &orig, const vec3 &dir, float &t0) const
{
    vec3 L = center - orig;
    float tca = L * dir;
    float d2 = L * L - tca * tca;
    if (d2 > radius * radius)
        return false;
    float thc = sqrtf(radius * radius - d2);
    t0 = tca - thc;
    float t1 = tca + thc;
    if (t0 < 0)
        t0 = t1;
    if (t0 < 0)
        return false;
    return true;
}
};

在球的结构体中，我们定义了 球心center，球半径radius，球的材质material，球类的构造函数。
ray_inersert()函数，该函数输入是源点orig，方向dir，和相交时间t0。返回的是从这个源点发出的，方向是dir的射线是否和当前球体相交。
一条射线可以由一个起点 orig 和一个方向 dir 表示：

一个点 center 到一条射线的距离计算方法如下：
1.获得射线起点到该点的向量 L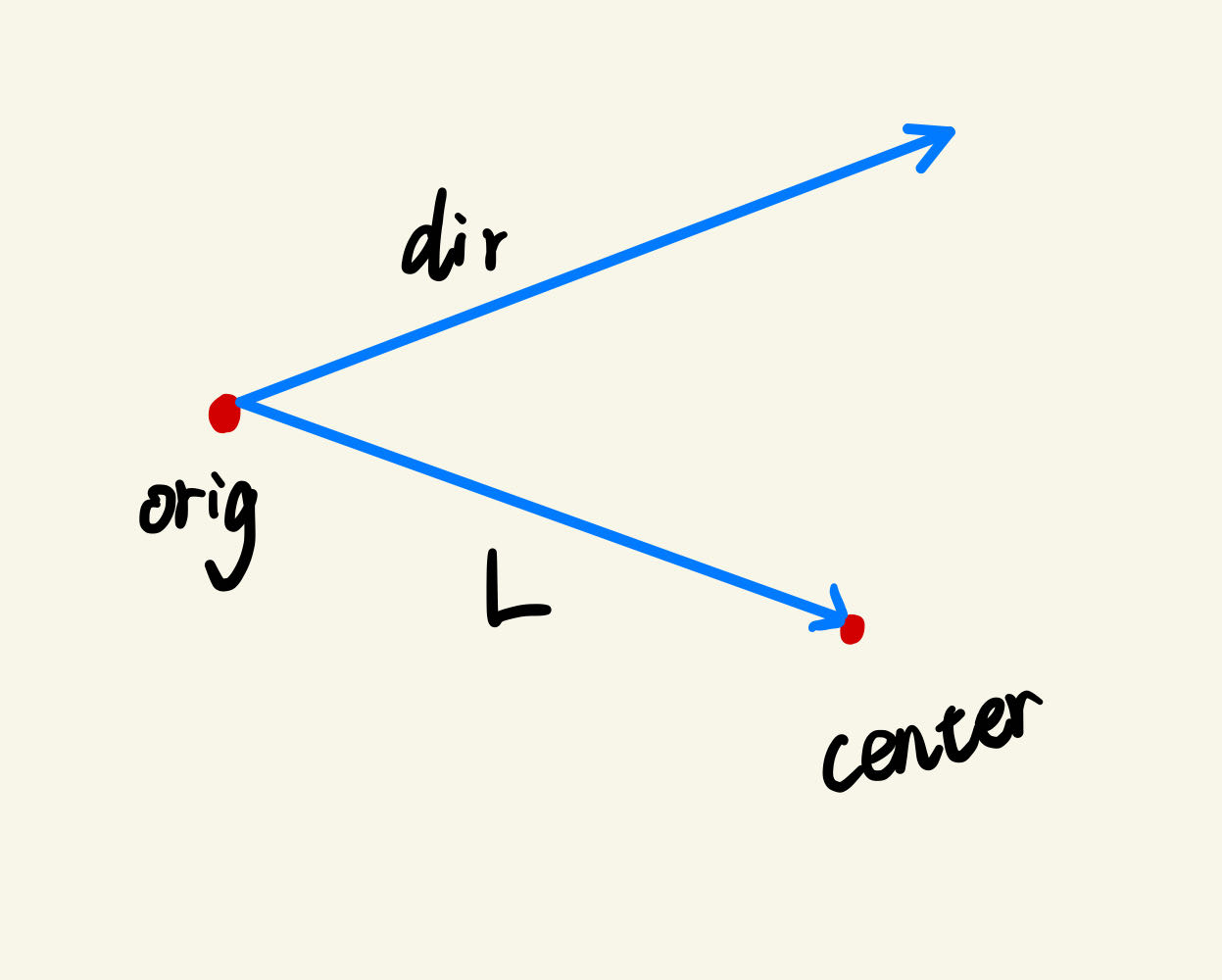

vec3 L = center - orig;

2.计算 L 在 dir 方向上的投影长度 tca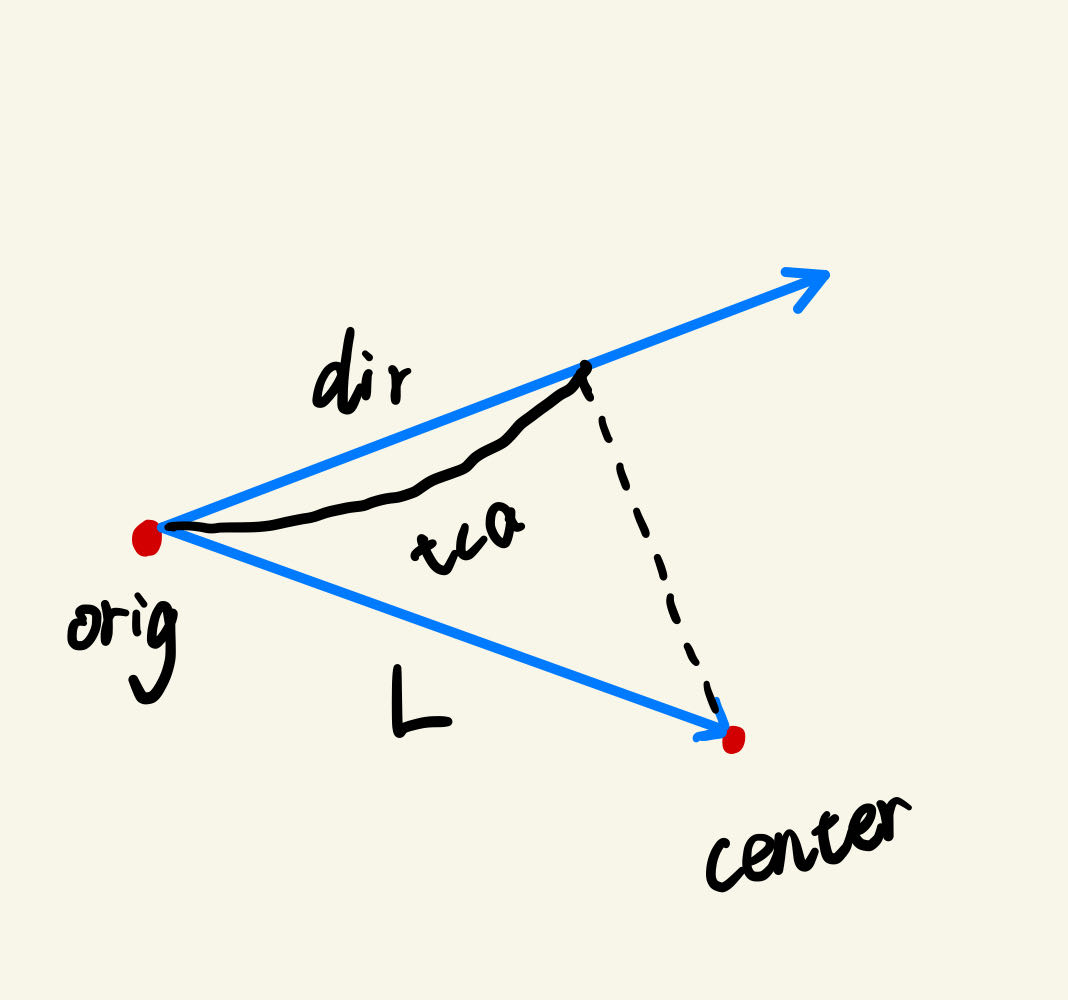

float tca = L * dir;

3.计算 center 到射线距离的平方 d2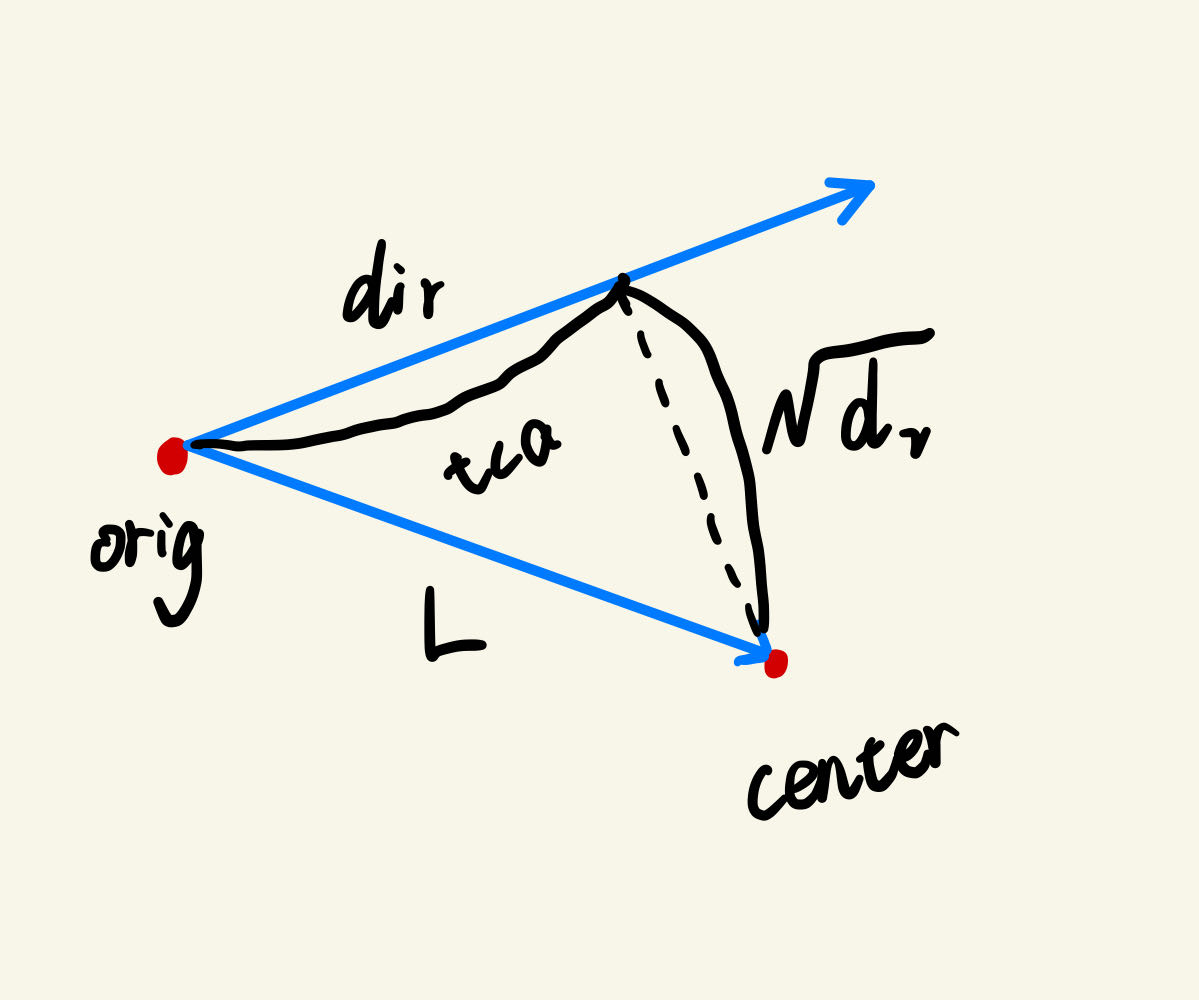

得到距离之后直接与球体半径判断即可，当距离大于球体半径时，说明射线与球体不相交，当距离小于等于球体半径时，说明射线与球体相交。
下面是求得t0和t1,从下图可以看到其实就是一个很基础的几何问题，由上面我们求到了球体中心点到射线的距离d2，所以用勾股定理便可以求到 thc 的长度。又因为上一节我们求到了 tca 的长度，所以 tca 分别加减 thc 便可以求到 t0 和 t1，因为是单位向量，所以时间就是t0和t1。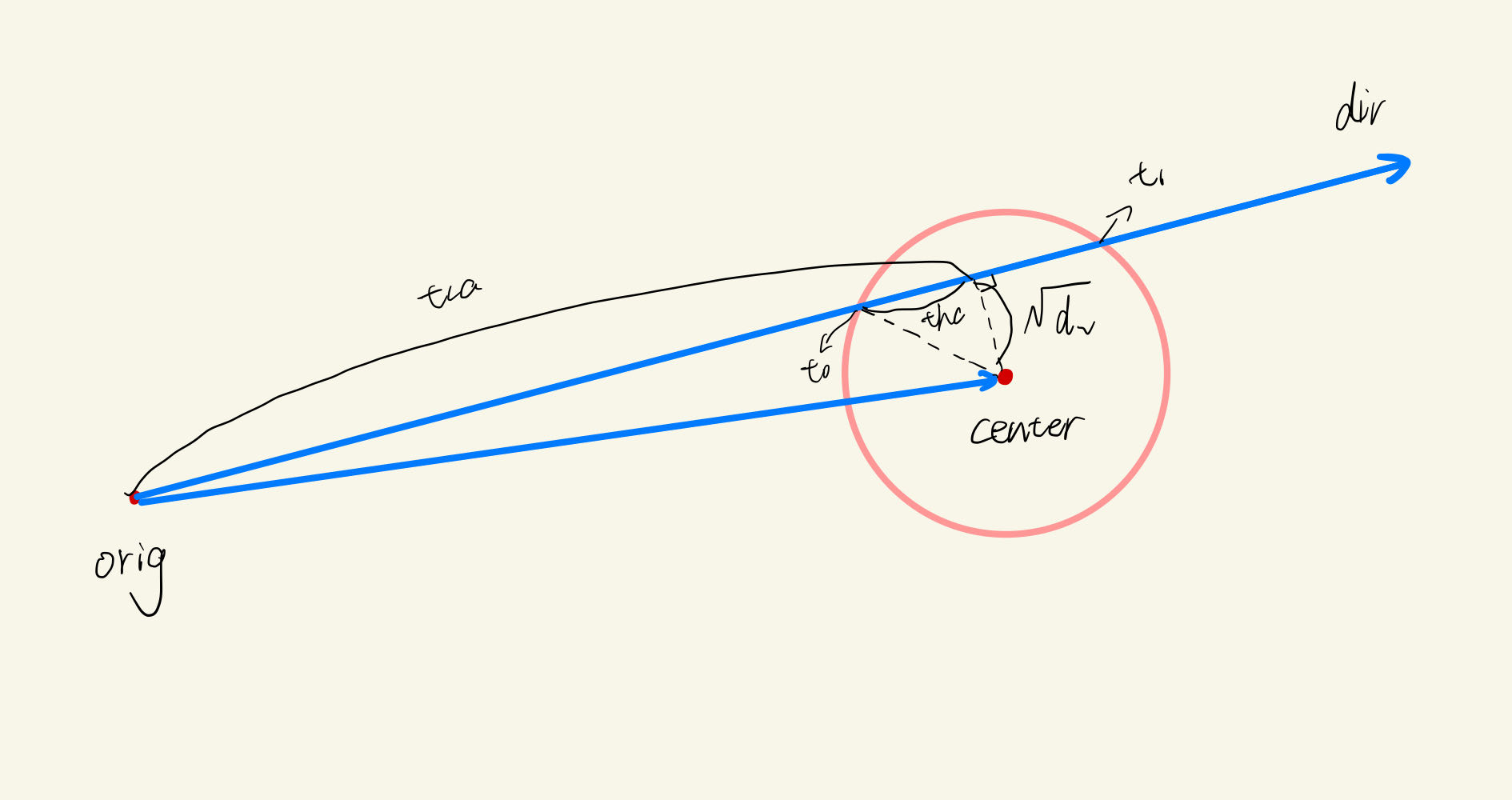

如果光线的出发点在球体外，那么按照上述方法得到的 t0 便是正确的相交时间。但是有一种特殊情况，如果光线的出发点在球体内部，那么上述方法得到的 t0 会是负值，所以我们需要判断一下 t0 是否小于 0，如果小于 0 则 t1 才是光线与球体表面相交的时间。
至此球体定义完毕

3.材质

struct Material
{
Material(const float &r, const vec4 &a, const vec3 &color, const float &spec) : refractive_index(r), albedo(a), diffuse_color(color), specular_exponent(spec) {}
Material() : refractive_index(1), albedo(vec4{1, 0, 0, 0}), diffuse_color(vec3{0, 0, 0}), specular_exponent(0) {}
float float refractive_index;//折射率
vec4 albedo;//光的各部分权重,漫反射，高光，反射，折射
vec3 diffuse_color;//材料本色
float specular_exponent;//高光系数;
};

不同的球体可以有不同的材质，所以我们定义一个材质结构 Material，其含有refractive_index折射率，一个四维向量 albedo 用于控制漫反射、高光、反射，折射产生的颜色强度，一个用于表示物体自身颜色的参数diffuse_color，一个specular_exponent高光系数。

4.光源

//光源
struct Light
{
    Light(const vec3 &p, const float &i) : position(p), intensity(i) {}
    vec3 position;//发光点位置
    float intensity;//发光强度
};

该结构体定义了，发光点位置position，发光点强度intensity.

5.反射函数

//反射函数，输入入射光，和法线方向，返回出射光
vec3 reflect(const vec3 &I, const vec3 &N)
{
    return I - N * 2.f * (I * N);  
}

反射函数，输入入射光，和法线方向，返回出射光
因为这里是镜面反射，所以入射光和反射光与法线的夹角是一样的，那么只需要用入射光的方向向量减去其在法线方向上的两倍投影长度的投影向量，即为镜面反射光的方向向量。为什么是减去两倍的方向向量，是因为反射光线等于两倍的红色向量加上入射光，然而红色向量和入射光在法线上面的投影方向相反，所以要加一个负号。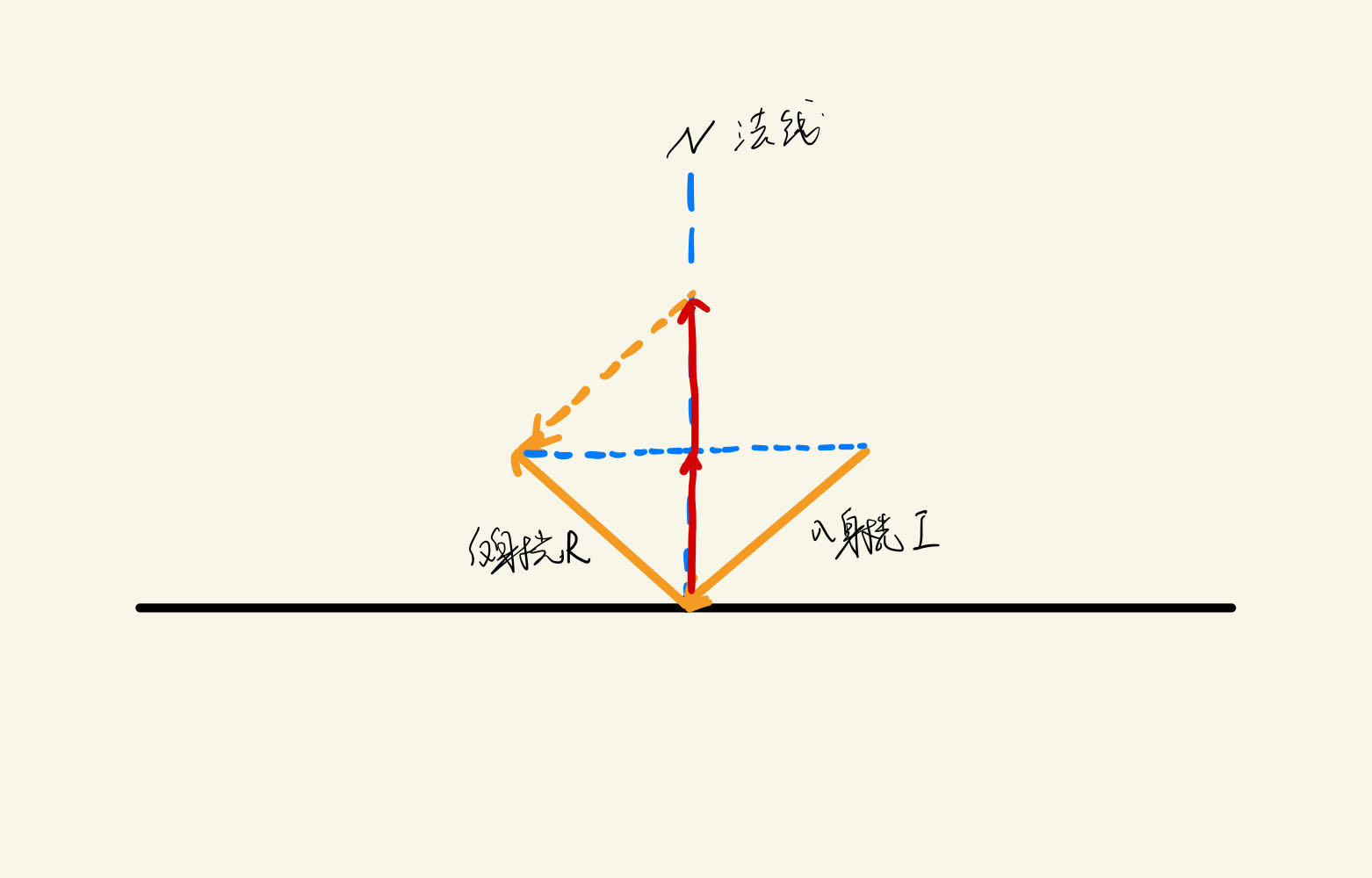

6.折射函数

vec3 refract(const vec3 &I, const vec3 &N, const float &refractive_index)
{ // Snell's law
    float cosi = -std::max(-1.f, std::min(1.f, I * N));
    float etai = 1, etat = refractive_index;
    vec3 n = N;
    if (cosi < 0)
    {
        cosi = -cosi;
        std::swap(etai, etat);
        n = -N;
    }
    float eta = etai / etat;
    float k = 1 - eta * eta * (1 - cosi * cosi);
    return k < 0 ? vec3{0, 0, 0} : I * eta + n * (eta * cosi - sqrtf(k));
}

折射函数，输入入射光，法线，折射率
光线打到物体表面时除了会发生反射，还可能会有一部分光线进入物体，我们称这种现象为折射，入射角和折射角之间的关系可以用斯涅尔定律来描述： ，其中 n1,n2 分别为两种介质的折射率， , 分别是入射光、折射光与界面法线的夹角，分别叫做入射角和折射角。
然后基于上述的斯涅尔定律公式单独实现一个用于计算折射向量的函数 refract，需要注意的是当光线从物体内部折射到空气中时，我们需要将折射率交换一下，并且将法线反向。即当其小于0的时候。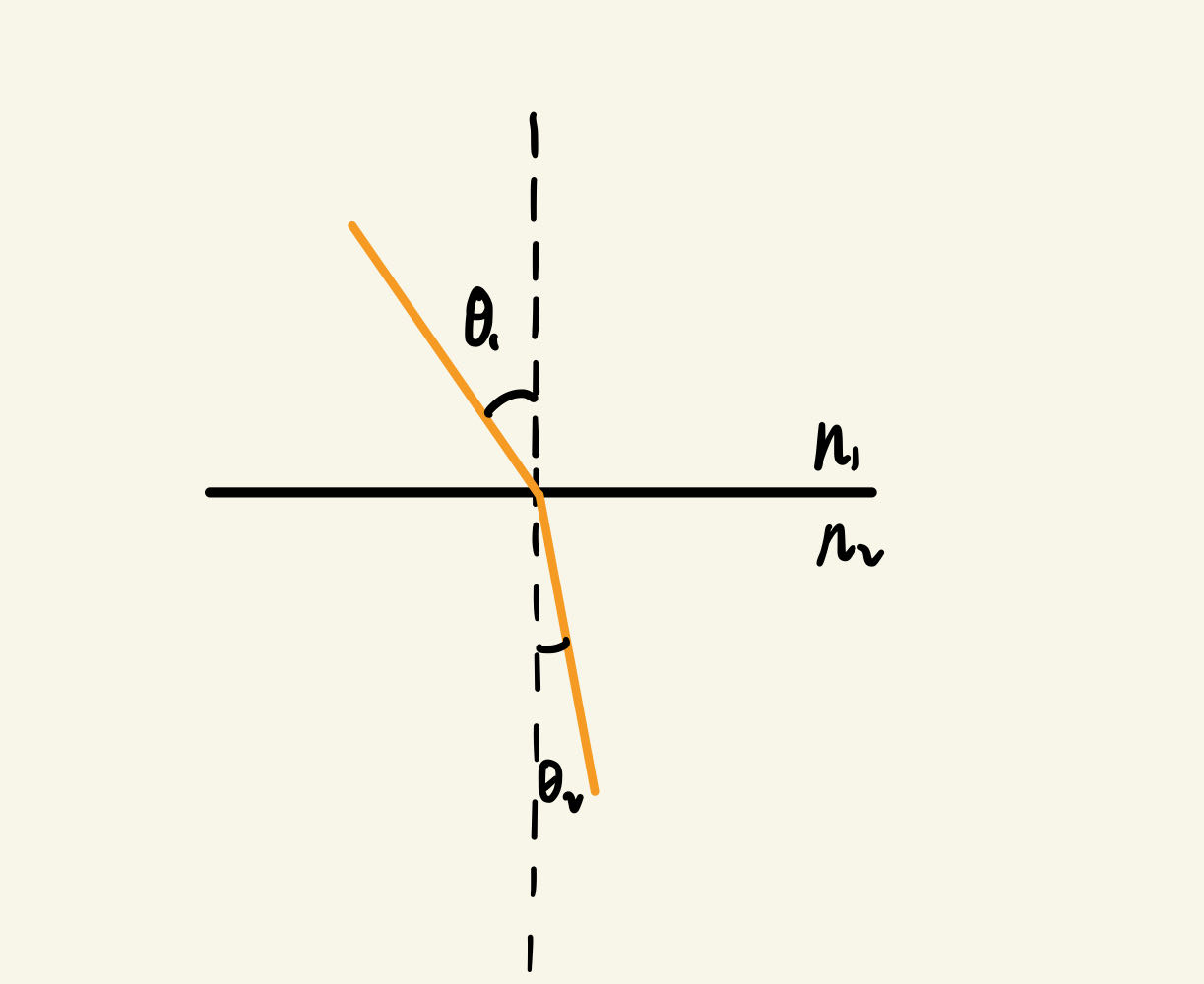

7.判断场景相交函数

bool scene_intersect(const vec3 &orig, const vec3 &dir, const std::vector<Box> &box, const std::vector<Sphere> &spheres, vec3 &hit, vec3 &N, Material &material)

该函数输入包括射线的源点坐标，射线方向方向向量dir,盒子结构体数组box[]，球体结构体数组spheres[],交点hit，交点材质material，交点的法向量N。返回bool,是否相交，如果相交同时得到交点坐标，交点材质，交点法向量，这 三个量都是通过引用变量得到的。

 float spheres_dist = std::numeric_limits<float>::max();

首先定义一个变量 spheres_dist 用于存储当前光线与场景中的球体最早相交的时间（其实这个时间意义上等同于距离），初始值为 float 的最大值。

for (size_t i = 0; i < spheres.size(); i++)
{
    float dist_i;//当前深度 
    if(i==2)//这个贴图是木质贴图
    if (spheres[i].ray_intersect(orig, dir, dist_i) && dist_i < spheres_dist)
    {
        spheres_dist = dist_i;
        hit = orig + dir * dist_i;
        N = (hit - spheres[i].center).normalize();
        material = spheres[i].material;
        material.diffuse_color = maps_picture(hit, spheres[i].center,1);
        continue;
    }
    if (i == 4)//这个贴图是地球贴图
        if (spheres[i].ray_intersect(orig, dir, dist_i) && dist_i < spheres_dist)
        {
            spheres_dist = dist_i;
            hit = orig + dir * dist_i;
            N = (hit - spheres[i].center).normalize();
            material = spheres[i].material;
            material.diffuse_color = maps_picture(hit, spheres[i].center,2);
            continue;
        }
    if (spheres[i].ray_intersect(orig, dir, dist_i) && dist_i < spheres_dist)
    {
        spheres_dist = dist_i;
        hit = orig + dir * dist_i;
        N = (hit - spheres[i].center).normalize();
        material = spheres[i].material;
    } 
}

然后遍历一遍球体数组 spheres[] ，依次判断是否相交，如果相交，同时判断相交时间是否小于spheres_dist，如果小于则说明当前的球体更早与光线相交，那么更新 spheres_dist 和 material。
这里给第三个球加上了木质纹理，给第五个球加上了地球纹理，加贴图的过程是，在返回交点的材质material的时候，不用该material本来的颜色，而是通过maps_picture这个函数输入交点的空间坐标和球的球心的看空间坐标，返回对应的二维坐标对应的贴图rgb颜色值。将这个点的贴图的rgb颜色值作为这个交点的matrial的rgb颜色值。这样就完成了贴图的工作。

//在z=-45处加棋盘格面
float checkerboard_dist = std::numeric_limits<float>::max();
if (std::abs(dir.z) > 1e-3)//避免垂直入射棋盘面
{                                    // avoid division by zero
    float d = -(orig.z + 45) / dir.z; // 棋盘面是z=-45
    vec3 pt = orig + dir * d;//交点坐标
    if (d > 1e-3 && fabs(pt.x) < 100 && pt.y < 300 && pt.y > -300 && d < spheres_dist)
    {
        checkerboard_dist = d;
        hit = pt;
        N = vec3{ 0, 0, 1 };
        material.diffuse_color = (int(.5 * hit.x + 1000) + int(.5 * hit.y)) & 1 ? vec3{ .3, .3, .3 } : vec3{ .3, .2, .1 };
    }
}

在这里我们为场景添加一个黄白相间的棋盘。添加棋盘只需要在场景相交检测时多检查一项即可，在这里我们假设棋盘位于 Z=−45 的位置。
类似检测光线与球体相交的过程，我们先定义一个用于记录棋盘距离变量checkerboard_dist，从观察点到棋盘的距离在 z方向的投影即为 orig.z + 45，那么根据方向 dir 便可以得到 d 的长度，同时可以求得光线与棋盘的交点。
有了距离和交点我们便可以判断光线是否与棋盘相交、是否在球体之前相交，以及设置棋盘黄白相间的颜色。
最后返回的是一个bool变量，判断当前是否是背景。距离大于1000是背景，小于1000则是前景。

8.投射光线函数

vec3 cast_ray(const vec3 &orig, const vec3 &dir, const std::vector<Box>& box,const std::vector<Sphere> &spheres, const std::vector<Light> &lights, size_t depth = 0)

该函数输入源点，射线方向，box数组，球体数组，光源数组，迭代深度初始为0.返回颜色值。

vec3 point, N;//交点，法线方向
Material material;
if (depth > 4||!scene_intersect(orig, dir, box,spheres, point, N, material))
{
    return vec3{0.48627,0.88627,0.69019}; // 返回背景色，浅绿色
}

函数内定义了交点point,交点的法向量N,交点的材质material。如果迭代深度超过4，或者与场景中的物体没有交点，则返回背景颜色，浅绿色。

//反射
vec3 reflect_dir = reflect(dir, N).normalize();//反射方向
vec3 reflect_orig = point + N*1e-3; // 沿着法线方向偏移一定距离，避免与自己相加
vec3 reflect_color = cast_ray(reflect_orig, reflect_dir, box,spheres, lights, depth + 1);
//折射
vec3 refract_dir = refract(dir, N, material.refractive_index).normalize();
vec3 refract_orig = refract_dir * N < 0 ? point - N * 1e-3 : point + N * 1e-3;
vec3 refract_color = cast_ray(refract_orig, refract_dir, box,spheres, lights, depth + 1);

这个像素点的颜色值包括空间内通过反射，和折射过来的光叠加形成的。首先通过reflect函数求得反射方向，为了防止之后使用cast_ray（）函数与自己相交，则将反射点沿着法线偏移一点。之后从该点，沿着反射方向，发射光线，获得反射点通过反射叠加的颜色值。。同理，通过refract()函数，求得折射方向，为了防止之后使用cast_ray（）函数与自己相交，则将折射点沿着法线偏移一点。之后从该点，沿着折射方向，发射光线，获得折射点通过折射叠加的颜色值。

float diffuse_light_intensity = 0, specular_light_intensity = 0;//漫反射强度，镜面反射强度
for (size_t i = 0; i < lights.size(); i++)//遍历光源
{
    vec3 light_dir = (lights[i].position - point).normalize();//光的传播方向，是这个光源和交点的连线
    float light_distance = (lights[i].position - point).norm();//光源和交点的距离

    vec3 shadow_orig = light_dir * N < 0 ? point : point + N * 1e-3; // 为了防止下一步中自己和自己相交，进行偏移处理
    vec3 shadow_pt, shadow_N;//
    Material tmpmaterial;
    //如果被遮挡则不进行该光源的光照计算，直接进行下一轮光源的计算，判断这个交点是否在这个光源的阴影中
    if (scene_intersect(shadow_orig, light_dir, box,spheres, shadow_pt, shadow_N, tmpmaterial) && (shadow_pt - shadow_orig).norm() < light_distance)
        continue;

    diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir * N);//phong模型中的理想漫反射，与视点无关
    specular_light_intensity += powf(std::max(0.f, reflect(light_dir, N) * dir), material.specular_exponent) * lights[i].intensity;//镜面反射（高光）
}

定义漫反射强度diffuse_light_intensity和镜面反射强度specular_light_intensity。上面遍历光源，求阴影的代码。遍历光源数组，通过判断光源和交点之间有无物体判断是否处在这个光源的阴影之中。最后将漫反射和镜面反射强度叠加起来。

return material.diffuse_color * diffuse_light_intensity * material.albedo[0] + vec3{1., 1., 1.} * specular_light_intensity * material.albedo[1] + reflect_color * material.albedo[2] + refract_color * material.albedo[3];
// //颜色*强度*系数

最后通过albedo[]数组里面的系数，将漫反射，镜面反射，反射，折射四种光融合起来。

9.渲染函数

本函数通过每一个像素发射光线，得到每一个像素点的值。最终生成相应大小的图片。
本实验设置图片宽为960，高度为600。下面代码，主要是两层循环，便利整个图片的所有像素点，求得这个像素点的空间坐标xyz,视点坐标是（0，0，0）然后求得方向（x,y,z）通过光线投射函数求得这个像素点的RGB颜色值，存入到framebuffer[]数组中。

 const int width = 960;                                                                                                   
 const int height = 600;
 const float fov = 1.05;//俯仰角
 std::vector<vec3> framebuffer(width * height);

 for (int j = 0; j < height; j++)
 {
     for (int i = 0; i < width; i++)
     {//前两层循环，便利每一个像素点
         float x = (i + 0.5) - width / 2.;
         float y = -(j + 0.5) + height / 2.;
         float z = -height / (2. * tan(fov / 2.));
         vec3 dir = vec3{x, y, z}.normalize();
         framebuffer[i + j * width] = cast_ray(vec3{0, 0, 0}, dir, box,spheres, lights);
     }
 }

我们采用直接生成图片，PPM 是一种非常简单的图片格式，选择此格式生成图片，下面对采用 P6 编码格式的 PPM 格式做一个简单的介绍。
P6 编码的 PPM 格式由两部分组成：头部分和图像数据部分
1.头部份
编码格式 + “\n” + 宽度 + " " + 高度 + “\n” + 最大像素值 + “\n”
本实验输出图像的宽度是960pixel，高度是600pixel，像素值是0到255

ofs << "P6\n"
    << width << " " << height << "\n255\n";

2. 图像数据部分

用 24 bits 代表每一个像素，红绿蓝分别占用 8 bits
举个例子，假设我们有一张宽度为 1024 ，长度为 768 的图片 out.ppm，那么我们看到的图片和文件中数据的对应关系应该是这样：

文件的第一行表示编码格式 P6，文件的第二行表示宽度 1024 和高度 768，文件的第三行表示最大像素值，设定为 255，此后图片每一个像素的 r g b 都分别由一个 8 bits 的数据表示，如图中的一小块白色的像素，那么它的颜色便被存成了 255 255 255。
下面代码是将图像数据写入文件，framebuffer[]数组中存储的是960×600个vec3结构体，每个结构体代表一个像素，每个结构体中的xyz分别代表像素的rgb三个值。下面代码是将每个像素的rgb三个值读出，然后归一化，输出到文件中。

for (size_t i = 0; i < height * width; ++i)
{
    vec3 &c = framebuffer[i];
    float max = std::max(c[0], std::max(c[1], c[2]));
    if (max > 1)
        c = c * (1. / max);//归一化
    for (size_t j = 0; j < 3; j++)
        {
            ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j])));
        }
}

10.读取RGB

Mat img, new_img1, new_img2;
int Rr[1000][1000], Gg[1000][1000], Bb[1000][1000];
int Rr1[1000][1000], Gg1[1000][1000], Bb1[1000][1000];//贴图1的RGB信息
int Rr2[1000][1000], Gg2[1000][1000], Bb2[1000][1000];//贴图2的RGB信息
void read_rgb()//交换红蓝
{
    for (int row = 0; row < new_img1.rows; row++)
    {
        for (int col = 0; col < new_img1.cols; col++)
        {      
            Rr1[row][col] = new_img1.at<Vec3b>(row, col)[2];
            Gg1[row][col]= new_img1.at<Vec3b>(row, col)[1];
            Bb1[row][col]=new_img1.at<Vec3b>(row, col)[0];
        }
    }
    for (int row = 0; row < new_img2.rows; row++)
    {
        for (int col = 0; col < new_img2.cols; col++)
        { 
            Rr2[row][col] = new_img2.at<Vec3b>(row, col)[2];
            Gg2[row][col] = new_img2.at<Vec3b>(row, col)[1];
            Bb2[row][col] = new_img2.at<Vec3b>(row, col)[0];
        }
    }
}

该函数通过定义三组全局数组，存储贴图的RGB信息，之后通过Mat类访问图片的每一个像素点。依次读取RGB。注意在图片中存储的顺序并不是RGB，而是BGR，读取每个分量时要注意顺序。

11.映射函数

vec3 maps_picture(vec3 point,vec3 center,int k) {
    float r = 0.0, g = 0.0, b = 0.0, u, v,pi=3.1415926;
    int nx, ny;
    //cout << "11" << endl;
    nx = 960;
    ny = 600;
//空间坐标映射到球坐标
    float X, Y, Z;
    Y = point.y - center.y;
    Z = point.z - center.z;
    X = point.x - center.x;
    float sum = sqrt(X * X + Y * Y + Z * Z);//归一化
    Y = Y / sum;
    X = X / sum;
    Z = Z / sum;
    auto phi = atan2(Z, X);
    auto theta = asin(Y);
    u = 1- (phi + pi) / (2 * pi);
    v = (theta+pi/2 ) / pi;
    int j = int((u)*nx);//求出像素索引
    int i = int((1-v) * ny - 0.001f);
    if (i < 0) i = 0;
    if (j < 0) j = 0;
    if (i > nx - 1) i = nx - 1;
    if (j > ny - 1) j = ny - 1;
 //返回对应贴图号的rgb的值
    if (k == 1) {
        r = ((float)Rr1[i][j]) / 255.0;
        g = ((float)Gg1[i][j]) / 255.0;
        b = ((float)Bb1[i][j]) / 255.0;
   }
    else if (k == 2) {
        r = ((float)Rr2[i][j]) / 255.0;
        g = ((float)Gg2[i][j]) / 255.0;
        b = ((float)Bb2[i][j]) / 255.0;
    }
    return vec3{r,g,b};
}

输入光线和物体的交点，球心坐标，贴图编号，返回对应二维坐标对应的贴图颜色值。
在直角坐标中，对于一个宽高为nx*ny的图片，坐标为( i , j ) (i,j)(i,j)的像素点的纹理坐标( u , v ) (u,v)(u,v)定义如下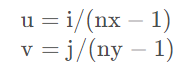

这样就能够将( i , j ) (i,j)(i,j)映射到( u , v ) (u,v)(u,v)，并缩放到[0,1]。
在球坐标中，我们同样可以将角度映射到( u , v )：假设( θ , ϕ )为球坐标上的一点，将球坐标想象成地球，则ϕ 为环绕着地轴旋转的角度（共360度），θ 为球心从北极点方向到南极点方向的角度（共180度），纹理坐标( u , v ) 为：

对于单位球表面上的一个命中点，球坐标转换到直角坐标的转换关系如下：

我们希望通过单位球上的命中点的直角坐标(x,y,z)，得到球坐标，变形得：

由于atan2的范围是，asin的范围是，为了最后输出为正数，且范围是0到1的数，要进行以下操操作：

注意在求xyz坐标时要将其标准化，因为要将y轴朝上，所以要进行减法操作。

12.主函数

首先读入两张贴图照片，地球和木头，读取两张图片的RGB值。

new_img1 = imread("C:\\Users\\lh\\Desktop\\code\\wood.jpg");
new_img2 = imread("C:\\Users\\lh\\Desktop\\code\\earthmap.jpg");
read_rgb();

主函数中定义了四种材料，紫色，红色材料，镜面，玻璃。

 Material purpel_material(1.0, vec4{0.4, 0, 0, 0.0}, vec3{0.58, 0.44, 0.86}, 50);
 Material red_material(1.0, vec4{0.3, 0.1, 0.0, 0.0}, vec3{1, 0,0}, 10);
 Material mirror(1.0, vec4{0.0, 10.0, 0.8, 0.0}, vec3{1.0, 1.0, 1.0}, 1425);
 Material glass(1.5, vec4{0.0, 0.5, 0.1, 0.8}, vec3{0.6, 0.7, 0.8}, 125);

添加五个球。

std::vector<Sphere> spheres;
spheres.push_back(Sphere(vec3{-3, 0, -16}, 2, purpel_material));
spheres.push_back(Sphere(vec3{-1.0, -1.5, -12}, 2, glass));
spheres.push_back(Sphere(vec3{6, -0.5, -18}, 3, red_material));
spheres.push_back(Sphere(vec3{-7, 5, -18}, 4, mirror));
spheres.push_back(Sphere(vec3{ -9, -5, -18 }, 3, red_material));

添加三个光源，光源结构体详见上面。

std::vector<Light> lights;
lights.push_back(Light(vec3{-20, 20, 20}, 1.5));
lights.push_back(Light(vec3{30, 50, -25}, 1.8));
lights.push_back(Light(vec3{30, 20, 30}, 1.7));

调用渲染函数，进行绘制，输入箱体数组，球体数组，光源数组。

render(box,spheres, lights);

三.结果展示，感悟总结

上图为最终的结果展示，上图一共生成了五个球体，每个球体的材质不同，一个棋盘平面，木制纹理和地球纹理主要通过贴图形成。从图片中可以看到生成了阴影效果，高光效果。每个球体有三个特别亮的部分即高光效果。左下角由于球体遮挡，光线较暗，右上角较为明亮。图中左上角球中绿色部分为远端不可达点。
经过本次实验，我了解了光线追踪的基本原理，了解了图形学的基本知识，通过实验，提高了自己代码水平。
水平有限，欢迎各位批评指正。
相关文件请见我的github:主页地址。
如果 图片展示不全，大家可以看我的语雀主页https://www.yuque.com/wangzhelingmengs/yag92e/qebalz65gspsfq5w?singleDoc# 《光线追踪实验报告》