反插值法求函数方程的根(内附代码及例题)

反插值法求函数方程的根matlab实现(内附代码及例题)

关于反插值法求函数方程根的相关理论，小编在这不加赘述啦。如果不清楚的小伙伴请自行百度或私聊小编～

下面先来张图(反插值法的图示):
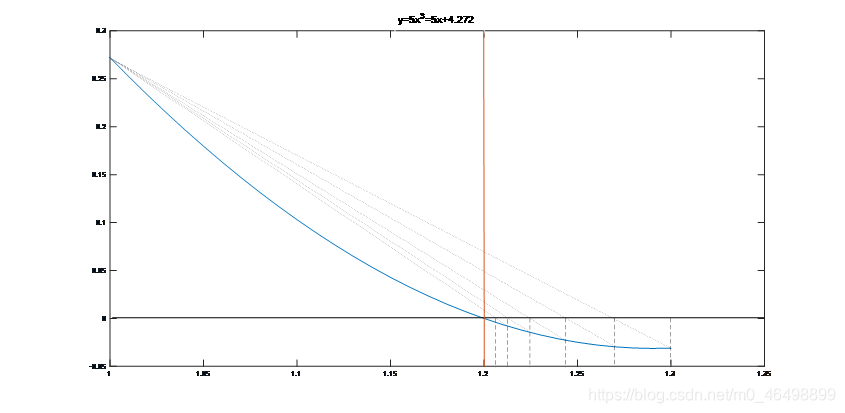敲黑板 ！！！重点来啦
matlab代码如下:

%%%% 反插值法法求函数方程的根 %%%%%
%%%%%      Liu Deping       %%%%%
%%%%%      2020.06.09       %%%%%
clc;
clear all
s=input('请输入函数表达式：f = ','s');
f=inline(s);
a = input('请输入区间左端点:a=');
b = input('请输入区间右端点:b=');
eps=input('请输入停止精度要求:eps=');  %%“|b-x|<=eps”
k=1;
x=(a*f(b)-b*f(a))/(f(b)-f(a));
fprintf('        k        a        f(a)       b        f(b)       xk        f(xk)\n ');
T=[k,a,f(a),b,f(b),x,f(x)];
while abs(T(k,4)-T(k,6))>eps/2
    k=k+1;
    if  f(x)*f(a)==0
        a=a;
        b=x;
        x=(a*f(b)-b*f(a))/(f(b)-f(a));
        T=[T;k,a,f(a),b,f(b),x,f(x)];
        break
    elseif  f(x)*f(a)>0
        a=x;
        b=b;
        x=(a*f(b)-b*f(a))/(f(b)-f(a));
        T=[T;k,a,f(a),b,f(b),x,f(x)];
    elseif  f(x)*f(a)<0
        a=a;
        b=x;
        x=(a*f(b)-b*f(a))/(f(b)-f(a));
        T=[T;k,a,f(a),b,f(b),x,f(x)];
    end
end
disp(T);
fprintf('经过%d次迭代，函数方程根的近似解为：x=%.8f\n',k-1,T(k-1,6))

下面给出例题

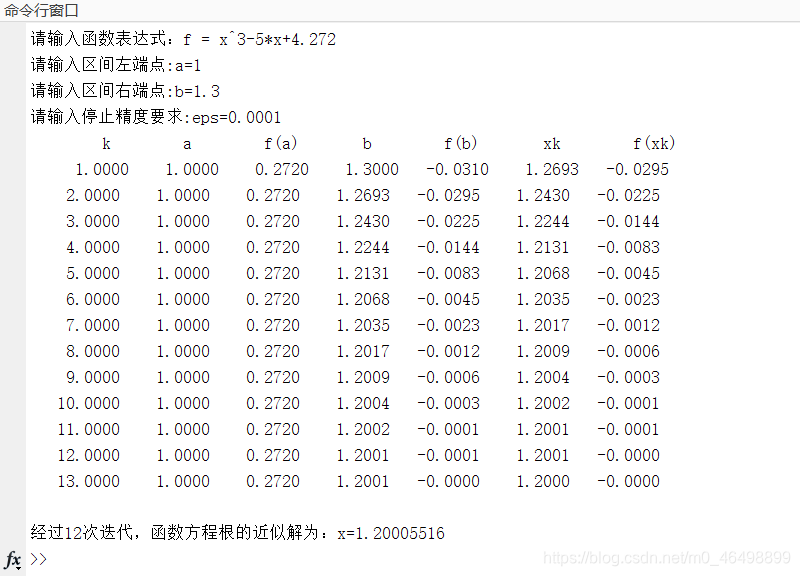
最后，希望小编的这段代码对大家有所帮助！同时，喜欢小编的小伙伴点个赞加个关注吧～小编将持续更新