中心极限定理（CLT）——matlab代码模拟验证

中心极限定理（CLT）：令，···，为均值为，方差为的IID序列，，则有

，该处箭头表示依分布收敛，其中，。

因此，如果存在IID序列X1,···,Xn，若Xi满足正态分布，则一个Xi就可以满足中心极限定理。如果IID序列X1,···,Xn，若Xi满足非正态分布的其他分布形式，则至少两个Xi才能满足中心极限定理。为了更直观地理解这个观点，我们通过matlab编写代码来进行验证。

假设IID序列X1,···,Xn，Xi满足均匀分布。先取matlab中的生成随机数函数rand()，满足[0,1]上的均匀分布，可以先简单绘出结果进行验证。

x=rand(1000000,1);
hist(x,50);

 可以看出基本生成的随机数是满足均匀分布的。

再来检验是否均值满足正态分布

subplot(2,2,1)
U=rand(10000,2);
Y=0.5*(U(:,1)+U(:,2));
hist(Y,50);
title('Subplot 1: (X1+X2)/2')
subplot(2,2,2)
U1=rand(10000,4);
Y1=sum(U1,2)/4;
hist(Y1,50);
title('Subplot 1: (X1+X2+X3+X4)/4')
subplot(2,2,3)
U2=rand(10000,8);
Y2=sum(U2,2)/8;
hist(Y2,50);
title('Subplot 1: (X1+X2+```+X8)/8')
subplot(2,2,4)
U3=rand(10000,16);
Y3=sum(U3,2)/16;
hist(Y3,50);
title('Subplot 1: (X1+X2+```+X16)/16')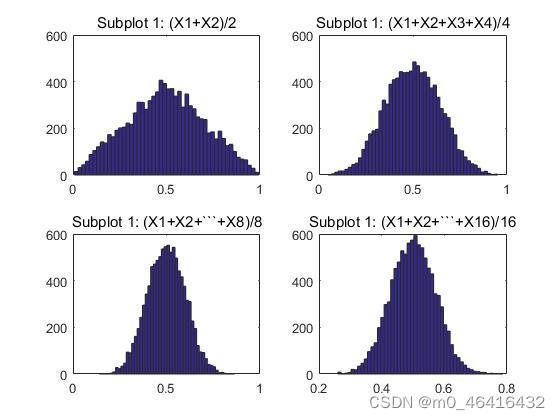

 

 可以看到，随着随机变量数量的增多，其平均值也越来越满足正态分布。同时从图中也可以看到频方图中峰值位于0.5处，为原来均匀分布均值的期望，这也侧面反映了大数定律，当样本数据增加时，会更加趋近于期望。