常见的排序方式
1、冒泡排序:
时间复杂度:最好情况是“O(n)”,最坏情况是“O(n2)”
空间复杂度:开辟一个空间交换顺序O(1)
2、快速排序:
时间复杂的:最好情况是“O(nlogn)”,最坏情况是“O(n2)”
空间复杂度:
最好的情况:每一次base值都刚好平分整个数组,递归树的深度O(logn)
最坏的情况:每一次base值都是数组中的最大/最小值,递归树的深度O(n)
3、插入排序
时间复杂度:最好情况是“O(n)”,最坏情况是“O(n²)”
空间复杂度:O(1)
4、希尔排序
时间复杂度:最好的情况O(n^(1.3)) 最坏的情况:O(n^(2))(与序列有关)
空间复杂度:O(1)
5、选择排序
时间复杂度:O(n^(2))
空间复杂度:O(1)
6、堆排序:
时间复杂度:
总时间为建堆时间+n次调整堆 —— O(n)+O(nlogn)=O(nlogn) 建堆时间:从最后一个非叶子节点遍历到根节点,复杂度为O(n) n次调整堆:每一次调整堆最长的路径是从树的根节点到叶子结点,也就是树的高度logn,所以每一次调整时间复杂度是O(logn),一共是O(nlogn)
空间复杂度
堆排序只需要在交换元素的时候申请一个空间暂存元素,其他操作都是在原数组操作,空间复杂度为O(1)
7、归并排序
时间复杂度:O(n⋅log2n)
空间复杂度:O(n)。
实现方式
1、冒泡排序
从第一个数开始往后两两比较,1和2比,2和3比……,如果是需要升序,则当后面的数比前面小时交换顺序。必到最后再从头开始继续比较,每次循环都能产生一个最大值,所以每轮比较次数会比上一次少一次。

代码
void Bubble_Sort(int arr[], int n) {
int flag = 1;
for (int i = 0; i < n - 1; i++) {
flag = 1;
for (int j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = 0;
}
}
if (flag == 1) {
break;
}
}
}
2、快速排序:
任取待排序序列的一个元素作为中心元素(可以用第一个,最后一个,也可以是中间任何一个),习惯将其称为pivot,枢轴元素;将所有比枢轴元素小的放在其左边;将所有比它大的放在其右边;形成左右两个子表;然后对左右两个子表再按照前面的算法进行排序,直到每个子表的元素只剩下一个。
假设以第一个元素39为中心元素, 然后定义两个指针分别指向第一个元素和最后一个元素

从右边开始,指针往右偏移,直到找到比39小的,然后将该数放到中心元素位置,然后左边指针开始向右偏移,找到比39大的,将该数放到右边指针停留的位置,然后右边指针再向左偏移,如此循环,


直到两个指针重合
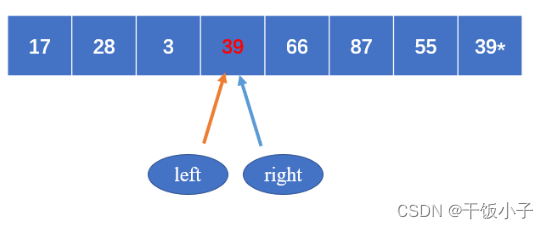
动态图如下
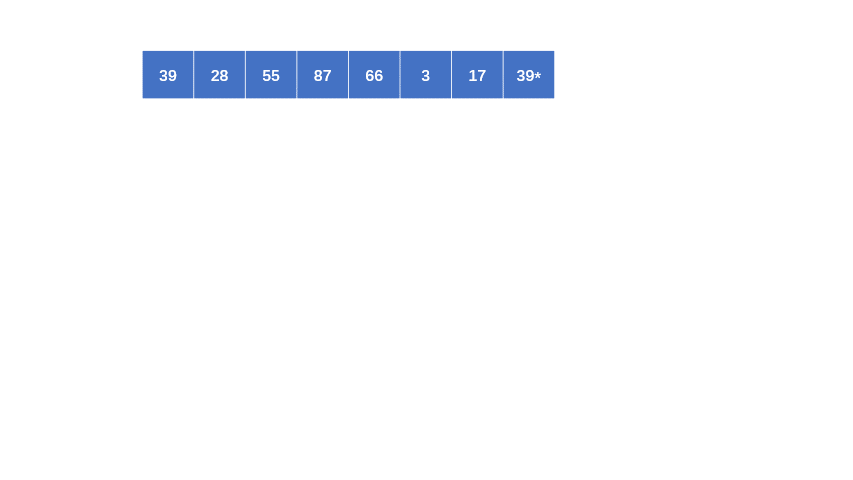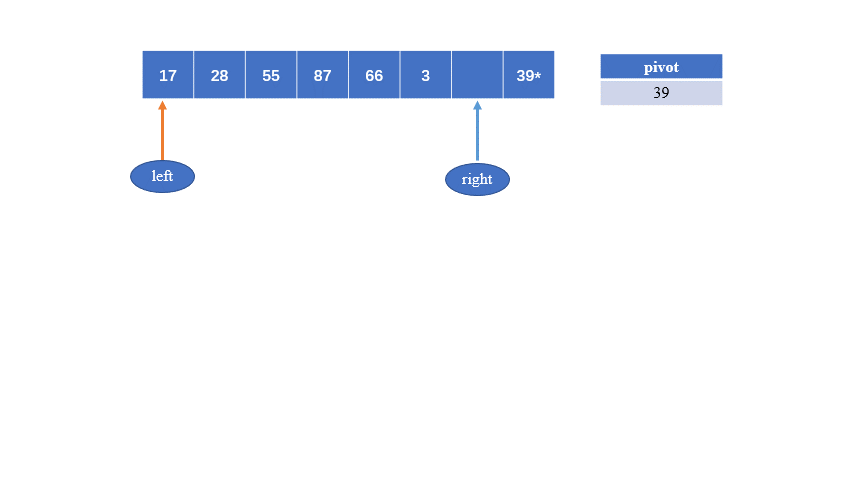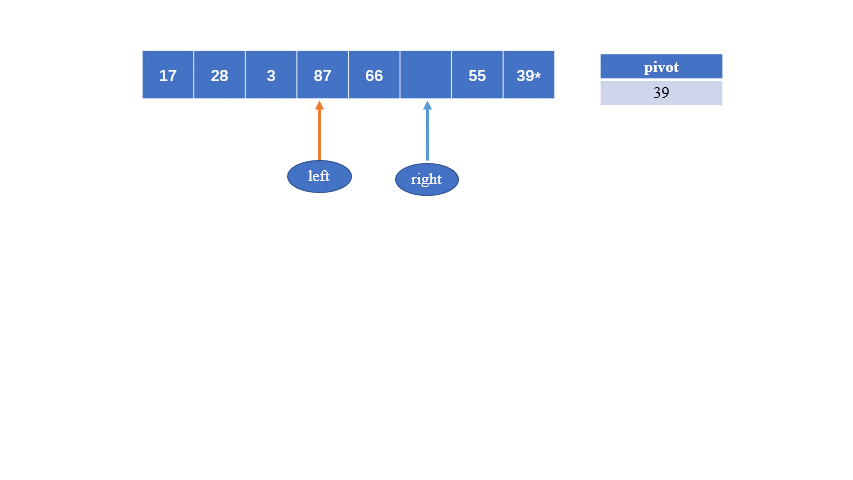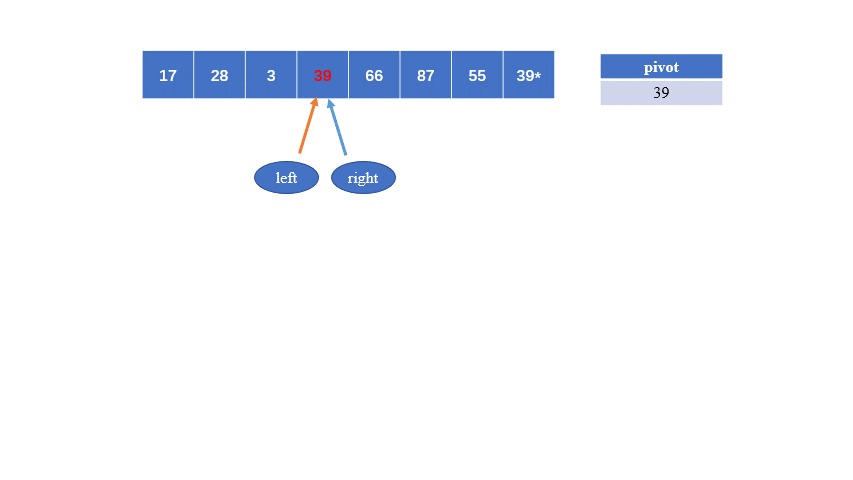
然后39将数组分为了左右两组,这两组再分别进行上面的操作
#include <stdio.h>
int find_pos(int a[], int low, int high)
{
int key = a[low];
while(low < high)
{
while(low < high && a[high]>=key)
{
high --;
}
a[low] = a[high];
while(low < high && a[low] <= key)
{
low ++;
}
a[high] = a[low];
}
a[low] = key;
return low;
}
void quick_sort(int a[], int low, int high)
{
if(low<high)
{
int pos = find_pos(a, low, high);
quick_sort(a, low, pos-1);
quick_sort(a, pos+1, high);
}
}3、插入排序
假设前面 n-1(其中 n>=2)个数已经是排好顺序的,现将第 n 个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。
#include <stdio.h>
void insert_sort(int a[], int n)
{
int key;
int j;
for(int i=1; i<n; i++)//控制无序序列元素的下标
{
key = a[i];
//找到key在有序序列中的位置
for(j=0; j<i; j++)
{
if(key <= a[j])
{
break;
}
}
//空出下标为j的位置
for(int k=i-1; k>=j; k--)
{
a[k+1] = a[k];
}
//将关键字key存放到下标为j的位置上
a[j] = key;
}
}4、希尔排序
希尔排序目的为了加快速度改进了插入排序,交换不相邻的元素对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
在此我们选择增量 gap=length/2,缩小增量以 gap = gap/2 的方式,用序列 {n/2,(n/2)/2...1} 来表示。



void ShellSort(int *num, int len)
{
int i, j, temp, step;
// 步长,每次循环缩小一倍
for (step = (len - 1) /2; step >= 1; step /= 2)
{
// 插入排序过程,从步长第二个数开始判断是否需要插入
for (i = step; i < len; i++)
{
if (num[i - step] > num[i])
{
temp = num[i];
for (j = i - step; num[j] > temp; j -= step)
{
num[j + step] = num[j];
}
num[j + step] = temp;
}
}
}
}
5、选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
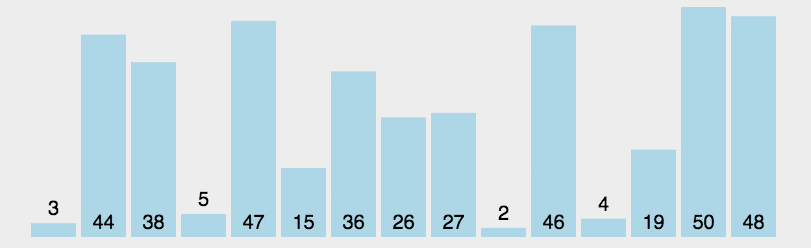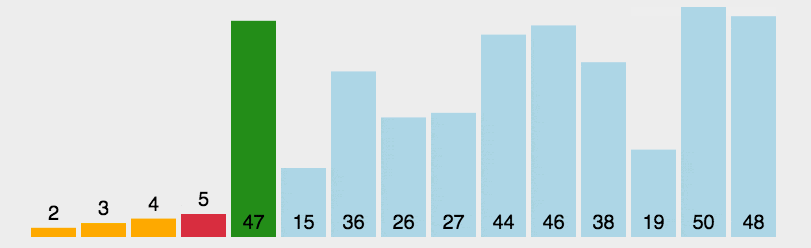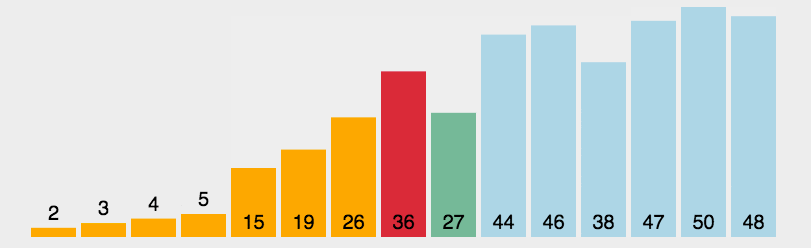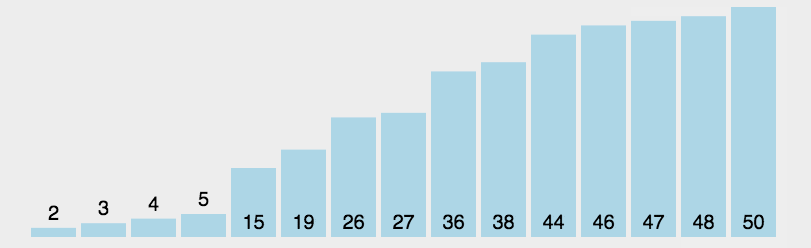
#include <stdio.h>
void select_sort(int a[], int n)
{
int min_index;
for(int i=0; i<n-1; i++)
{
min_index = i;
for(int j=i+1; j<n; j++)
{
if(a[j] < a[min_index])
{
min_index = j;
}
}
if(min_index != i)
{
int temp = a[min_index];
a[min_index] = a[i];
a[i] = temp;
}
}
}
6、堆排序
要求:有一个数组{4,6,8,5,9},要求使用堆排序法,将数组升序排序
一、
1.假设给定无序序列结构如下

2.此时我们从最后一个非叶子节点开始(叶节点自然不用调整,第一个非叶子节点arr.length/2-1=5/2-1=1,也就是下面的节点),从左至右,从下至上进行调整,观察6的两个子节点,从右至左,9大于6就和6互换
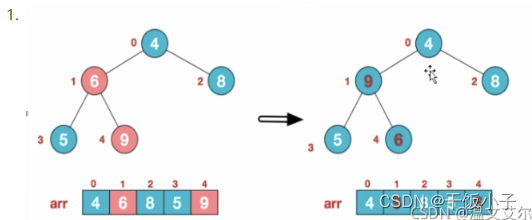
3.找到第二个非叶子节点4,由于[4,9,8]中9元素最大,4和9交换

4.此时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6

5.此时我们就将一个无序序列构造成了一个大顶堆
二、
将堆顶元素与末尾元素进行交换,使末尾元素最大,然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素,如此反复进行交换,重建,交换
1.将堆顶元素9和末尾元素4进行交换

2.重新调整结构,使其继续满足堆定义

3.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8

4.后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

#include <stdio.h>
#define size 10
void Swap(int *num, int i, int j)
{
int temp;
temp = num[i];
num[i] = num[j];
num[j] = temp;
}
// 最大堆调整
void Heapify(int *num, int len, int k)
{
if (k < len)
{
int root = k; // 根结点
int lchild = 2*k + 1; // 左孩子结点
int rchild = 2*k + 2; // 右孩子结点
// 查找左右孩子结点中的最大结点
if (lchild < len && num[root] < num[lchild])
{
root = lchild;
}
if (rchild < len && num[root] < num[rchild])
{
root = rchild;
}
// 交换最大结点到根结点
if (root != k)
{
Swap(num, root, k);
// 每次交换都可能影响到对应孩子结点子树的顺序
// 所以需要对交换后的孩子结点子树进行最大堆调整
Heapify(num, len, root);
}
}
}
// 创建最大堆
void CreateHeap(int *num, int len)
{
int i;
// 最后一个结点下标
int last = len - 1;
// 最后一个结点的父结点下标
int parent = (last - 1) / 2;
// 从最后一个结点的父结点到根结点,依次进行最大堆调整
for (i = parent; i >= 0; i--)
{
Heapify(num, len, i);
}
}
// 堆排序
void HeapSort(int *num, int len)
{
// 创建最大堆并进行最大堆调整
CreateHeap(num, len);
printf("最大堆调整!\n");
int i;
// 依次取出根结点(最大值)
for (i = len - 1; i >= 0; i--)
{
// 将最大堆的根结点(最大值)换到最后一个结点
Swap(num, i, 0);
// 交换后二叉树的根结点发生了改变,故还需对根结点做最大堆调整(已交换的末尾结点不参与调整)
// 而此时根结点小于所有父结点,因而在调整时只需考虑最大孩子的分支即可
Heapify(num, i, 0);
}
}
int main()
{
int i, num[size] = {8, 4, 3, 1, 6, 9, 5, 7, 2, 0};
HeapSort(num, size);
for (i = 0; i < size; i++)
{
printf("%d ", num[i]);
}
printf("\n");
return 0;
}
7、归并排序
- 递归分解,将数组分解成left和right。如果这两个数组内部数据是有序的。如果无序,则对数组进行二分,直至分解出的小组只有一个元素,此时认为该小组内部有序
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾

#include <cstdio>
void merge(int a[],int l,int r,int mid,int n){//归并的"治"的过程,将两个有序序列合并为1个有序序列
//l->最左边的元素下标,r->最右边的元素下标,mid->中间元素下标,temp[]是临时数组,n是a[]长度
int temp[n];
int i=l;//左序列指针
int j=mid+1;//右序列指针
int k=0;//临时数组指针
while(i<=mid&&j<=r){
if(a[i]<=a[j])
temp[k++]=a[i++];
else
temp[k++]=a[j++];
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[k++]=a[i++];
}
while(j<=r){//将右边剩余元素填充进temp中
temp[k++]=a[j++];
}
k=0;
//将temp中的元素全部拷贝到原数组中
while(l<=r)
a[l++]=temp[k++];
}
void merge_sort(int a[],int l,int r){//归并排序,“分而治之”的过程,递归实现
if(l>=r)//保证l是左边,r是右边 n是a[]长度
return ;
int mid=(l+r)/2;
//将序列分为两个序列,分别排序
merge_sort(a,l,mid);//左边归并排序,使左子序列有序
merge_sort(a,mid+1,r);//右边归并排序,使右子序列有序
merge(a,l,r,mid,r-l+1);//将两个有序子序列合并
}
int main(){
int a[105],n,i;
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d",&a[i]);
merge_sort(a,0,n-1);
for(i=0;i<n;i++)
printf("%d",a[i]);
return 0;
}























 1674
1674

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








