线性时间排序

最新推荐文章于 2023-10-04 18:01:50 发布

原创最新推荐文章于 2023-10-04 18:01:50 发布 · 316 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

基础算法专栏收录该内容

8 篇文章

订阅专栏

说明：比较排序算法的复杂度下界是 O(nlog(n))

一、计数排序（复杂度是O(n)）

计数排序要求被排序元素都是整数型变量，即元素能用数组的指标表示

（1）统计个元素 i 的个数

（2）计算不超过 i 包括 i 的元素的个数

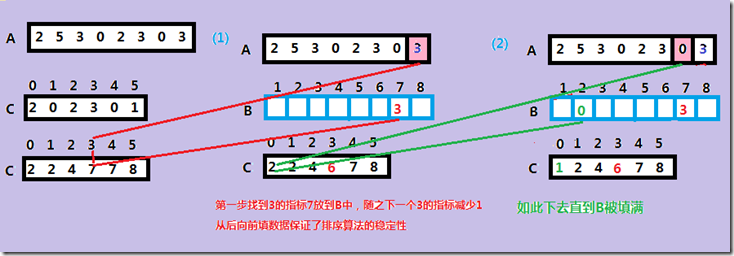
（3）将元素 i 放入适当的位子。

算法复杂度第一大步统计数字是n+k，其中k表示数字可能取到的最大的数

第二步需要复杂度是O(n),因此总的复杂度是 O(n+k). 当k=O(n)时，复杂度是O(n).

代码1：

#include<iostream>
using namespace std;

void COUNTING_SORT(int*a, int *b, int n)
{
	int c[10] = { 0 };
	for (int i = 0; i < n; i++)//记录c的序号（即a中数组元素）出现的次数
		c[a[i]] = c[a[i]] + 1;
	for (int i = 1; i <=n; i++)//序号所对应的值累加
		c[i] = c[i] + c[i - 1];
	for (int i = n-1; i>=0; i--)//按照序号的大小将所对应的值赋给b，计入数组下标应从0开始，因此用C[A[j]]减去1
	{
		b[c[a[i]]-1] = a[i];
		c[a[i]] = c[a[i]] - 1;
	}
}



void Print(int *a, int n)
{
   for (int i = 0; i<n; i++)
	 {
		cout<<a[i]<<" ";
	 }
   cout << endl;
}

int main()
{
	int a[9] = { 5, 4, 9, 1, 7, 6, 2, 3, 8 };
	int b[9] = {0};
	cout << "原序列：" << endl;
	Print(a, 9);
	COUNTING_SORT(a, b, 9);/*排好序的结果*/
	cout << "已排序列：" << endl;
	Print(b, 9);


	system("pause");
	return 0;
}

代码2：

#include <iostream>
using namespace std;
//此程序是实现计数排序算法，要特别注意指标问题
void COUNTING_SORT(vector<int> A, vector<int>& B, int k);

void COUNTING_SORT(vector<int> A, vector<int>& B, int k)
{
	vector<int> C(k + 1, 0);
	//统计A中重复元素的个数，C的指标表示这个元素的值，C的值表示对应元素的个数
	for (int j = 0; j<A.size(); j++)
		C[A[j]] = C[A[j]] + 1;
	//统计这个值在数组中的放置的位置，即排在第几位
	for (int i = 1; i <= k; i++)
		C[i] = C[i] + C[i - 1];
	//一次将A中的每个元素放到正确的位置，计入数组下标应从0开始，因此用C[A[j]]减去1
	for (int j = A.size() - 1; j >= 0; j--)
	{
		B[C[A[j]] - 1] = A[j];
		C[A[j]] = C[A[j]] - 1;
	}
}

void Print(vector<int>a)
{
	vector<int>::iterator iter = a.begin();
	for (; iter != a.end();)
		cout << *iter++ << " ";
	cout << endl;

}
int main()
{
	int a[] = { 1, 4, 3, 2, 0, 4, 3, 5, 7, 5, 4, 6, 7, 8, 5, 9, 6, 4, 3, 4, 0 };
	int k = 9;
	vector<int> A(a, a + 20);
	vector<int> B(20, 0);
	cout << "原始数据：" << endl;
	Print(A);
	COUNTING_SORT(A, B, k);
	vector<int>::iterator i;
	cout << "已排序结果：" << endl;
	Print(B);
	system("pause");
	return 0;
}

二、基数排序（是基于计数排序的算法）

对于比较大的一列整数，如329，457，736，823，67，384如果用计数排序就不能用了，因为k很大

这时可以使用基数排序，即按照位依次排，如下图所示

每一步用一次计数排序

假设数的位数是d，有n个数，则总的算法复杂度是 O(d(n+k)) 这里的k<9

复杂度关于 n 几乎是线性关系。

代码：

#include<iostream>
using namespace std;

void exchange(char** str, int j);
void char_bubble_sort(char** str, int d, int len);
void radix_sort(char** str, int d, int len);

void exchange(char** str, int j)
{
	char* tmp;
	tmp = str[j];
	str[j] = str[j + 1];
	str[j + 1] = tmp;
}
//对基数排序中的每趟排序使用冒泡排序  
void char_bubble_sort(char** str, int d, int len)
{
	for (int i = 0; i<len; i++)
	for (int j = 0; j<len - 1; j++)
	{
		if (str[j][d]>str[j + 1][d])
		{
			exchange(str, j);
		}
	}
}
//基数排序  
void radix_sort(char** str, int d, int len)
{
	for (int i = d - 1; i >= 0; i--)
	{
		char_bubble_sort(str, i, len);
	}
}
void Print(char **a, int n)
{
   for(int k=0; k<n; k++)
	{
	    if(k!=15)
		printf("%s ",a[k]);
		else
		printf("%s",a[k]);
	}
    cout << endl;
}
int main()
{
	char* str[16]={"COW","DOG","SEA","RUG","ROW","MOB","BOX","TAB","BAR","EAR","TAR","DIG","BIG","TEA","NOW","FOX"};  
	cout << "原始数据：" << endl;
	Print(str, 16);
	radix_sort(str,3,16);  
	cout << "已排序结果：" << endl;
	Print(str, 16);

	system("pause");
	return 0;
}

三、桶排序（期望时间复杂度O(n)）

桶排序算法想法类似于散列表

首先要假设待排序的元素输入符合某种均匀分布，例如数据均匀分布在[ 0,1）区间上.

则可将此区间划分为10个小区间，称为桶，每个桶存放一个链表，对散布到同一个桶

中的元素在排序。

代码：

#include<iostream>  
#include<algorithm>  
#include<math.h>  
using namespace std;
int a[100];
int b[100];
int c[100];
//定义桶对象  
class Bucket{
public:
	float d;
	Bucket* next;
	Bucket(){}
	Bucket(float d){
		this->d = d;
	}
}*bucket[11];
//计数排序  
void conunting_sort(int *a, int *b, int k, int len){
	//初始化c数组  
	for (int i = 1; i <= k; i++)
		c[k] = 0;
	//对a中元素出现次数的统计  
	for (int j = 1; j <= len; j++)
		c[a[j]]++;
	//对c进行累加，得到位置信息  
	for (int x = 1; x <= k; x++)
		c[x] += c[x - 1];
	//使用位置信息顺序重建数组  
	for (int y = len; y >= 1; y--){
		b[c[a[y]]] = a[y];
		c[a[y]]--;
	}
	for (int z = 1; z <= len; z++){
		a[z] = b[z];
	}
}

void exchange(char** str, int j){
	char* tmp;
	tmp = str[j];
	str[j] = str[j + 1];
	str[j + 1] = tmp;
}
//对基数排序中的每趟排序使用冒泡排序  
void char_bubble_sort(char** str, int d, int len){
	for (int i = 0; i<len; i++)
	for (int j = 0; j<len - 1; j++){
		if (str[j][d]>str[j + 1][d]){
			exchange(str, j);
		}
	}
}
//基数排序  
void radix_sort(char** str, int d, int len){
	for (int i = d - 1; i >= 0; i--){
		char_bubble_sort(str, i, len);
	}
}
//对桶排序的每趟使用冒泡排序  
void link_bubble_sort(Bucket* buck){
	Bucket *t, *tn;
	float s;
	for (Bucket* p = buck; p->next != NULL; p = p->next){
		for (Bucket* q = buck; q->next->next != NULL; q = q->next){
			if (q->next->d > q->next->next->d){
				s = q->next->next->d;
				q->next->next->d = q->next->d;
				q->next->d = s;
			}
		}
	}
}
//桶排序  
void bucket_sort(float *a, int len){
	//分桶  
	for (int i = 0; i<len; i++){
		Bucket *p;
		for (p = bucket[int(11 * a[i])]; p->next != NULL; p = p->next);
		p->next = new Bucket(a[i]);
	}
	//没个桶内进行排序  
	for (int j = 0; j<len; j++){
		link_bubble_sort(bucket[j]);
	}
	for (int k = 0; k<len; k++){
		for (Bucket *q = bucket[k]; q->next != NULL; q = q->next){
			printf("%.2f ", q->next->d);
		}
	}
	printf("\n");
}

int main(){
	/*int len;
	 char* str[16]={"COW","DOG","SEA","RUG","ROW","MOB","BOX","TAB","BAR","EAR","TAR","DIG","BIG","TEA","NOW","FOX"};  */
	/*  scanf("%d",&len);
	for(int i=1; i<=len; i++){
	scanf("%d",&a[i]);
	}
	conunting_sort(a,b,len,len);
	for(int j=1; j<=len; j++){
	if(j!=len)
	printf("%d ",a[j]);
	else
	printf("%d\n",a[j]);
	}*/

	float a[11] = { 0.21, 0.12, 0.39, 0.72, 0.94, 0.78, 0.17, 0.23, 0.26, 0.68, 0.11 };
	for (int z = 0; z<11; z++){
		bucket[z] = new Bucket();
	}
	bucket_sort(a, 11);



	 /* radix_sort(str,3,16);  
	  for(int k=0; k<16; k++){
	if(k!=15)
	printf("%s ",str[k]);
	else
	printf("%s\n",str[k]);
	}*/
	
	system("pause");
	return 0;
}