充电桩的收益（合肥市第39届信息学竞赛（2022年））

一、题目：

题目描述 Description

小可可在小区里安装了一个电动汽车充电桩，将自家充电桩的空闲时间开放给其他电动车用户付费使用。这种共享充电模式能充分提高闲置充电桩的利用率，既可以让小可可获得收益，也缓解了其他车主的充电焦虑。现在共有n个使用充电桩的申请,编号从0到n-1.小可可将按编号顺序依次处理所有申请，每个申请Qi（0<=i<=n-1）信息包含两个正整数ai和bi。
对于申请Qi小可可有两种处理策略：
（1）接受申请Qi，将获得ai元收益，但必须放弃接下来的bi个申请。
（2）拒绝申请Qi，没有收益，继续处理下一个申请。
请帮助小可可计算出共享充电桩的能获得的最大收益。

输入描述 Input Description

输入共n+1行；
第1行：一个整数n，表示使用充电桩的申请数量；
第2行到第n+1行：每行两个整数ai和bi；
表示接受申请Qi，将获得ai元收益，但必须放弃接下来的bi个申请。

输出描述 Output Description

输出共1行，一个正整数，表示小可可共享充电桩获得的最大收益。

样例输入 Sample Input

4 3 2 5 4 4 4 3 5

样例输出 Sample Output

6

数据范围及提示 Data Size & Hint

样例解释：
小可可共收到4个使用充电桩的申请，最佳策略为接受申请0和申请3。
（1）接受申请0，获得3元收益，但接下来的两个申请必须拒绝；
（2）接受申请3，获得三元收益；
总收益为：3元+3元=6元

数据范围：

1<=n<=1000000，1<=ai,bi<=100000;
20%数据：1<=n<=20 1<=ai<=500 1<=bi<=10
40%数据：20<=n<=2000 500<=ai<=20000 10<=bi<=100
60%数据：2000<=n<=100000 20000<=ai<=50000 100<=bi<=200
100%数据：100000<=n<=1000000 50000<=ai<=100000 200<=bi<=2500

二、分析：

看题目，100%数据 最多有1000000个申请，每个申请收益最多100000，最少跳过200个申请。

可以搜索！

搜索函数里，注意判断这条申请是否超过了申请个数。如果是，返回0

否，在"放弃，查看下一个申请" 和 "接受，获得a[i]收益，跳过b[i]中取最大值"中取最大值。

代码：

#include<iostream>
#include<cstring>
using namespace std;
const int MAX=1000005;
int n,a[MAX],b[MAX];//a[]:收益,b[]:放弃申请个数
int f(int x){//搜索
    if(x>n) return 0;//超出
    return max(f(x+1),f(x+b[x]+1)+a[x]);//f(x+1)是放弃当前申请,f(x+b[x]+1)+a[x]是接受申请
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%d%d",&a[i],&b[i]);
    }
    cout<<f(1);//从1开始
    return 0;
}

但是……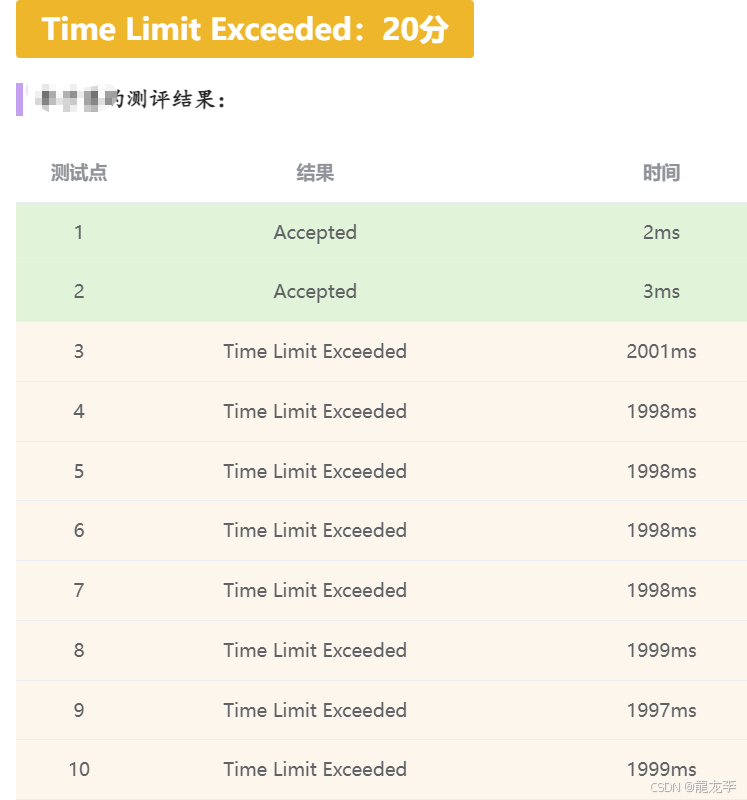

WHY？

100%数据：100000<=n<=1000000 50000<=ai<=100000 200<=bi<=2500

OH，原来n最大是 1000000，递归肯定超时！

怎么办呢？

下面隆重登场的是——记忆化搜索！

啥是记忆化搜索？

记忆化搜索可以将搜索时一些不必要的运算“剪掉”。

在这题中，可能已经算过。

所以我们把算过的记录。

若递归调用到算过的，把记录的值输出就行了！

代码：

#include<iostream>
#include<cstring>
using namespace std;
const int MAX=1000005;
int n,a[MAX],b[MAX],w[MAX];//w数组是记忆化数组
int f(int x){
    if(x>n) return 0;//边界
    if(w[x]!=-1) return w[x];//已经算过了
    return w[x]=max(f(x+1),f(x+b[x]+1)+a[x]);
}
int main(){
    cin>>n;
    memset(w,-1,sizeof(w));//清为-1，因为题目中返回值可能是0
    for(int i=1;i<=n;i++){
        scanf("%d%d",&a[i],&b[i]);
    }
    cout<<f(1);//顺推
    return 0;
}

方2：

动态规划

可以倒推

#include<iostream>
using namespace std;
int a[1000005],b[1000005],f[1010005],n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%d%d",&a[i],&b[i]);
    }
    for(int i=n;i>=1;i--){
        f[i]=max(f[i+1],f[i+b[i]+1]+a[i])//跟记忆化函数一样的功能，不用剪掉无用运算
    }
    cout<<f[1];
    return 0;
}

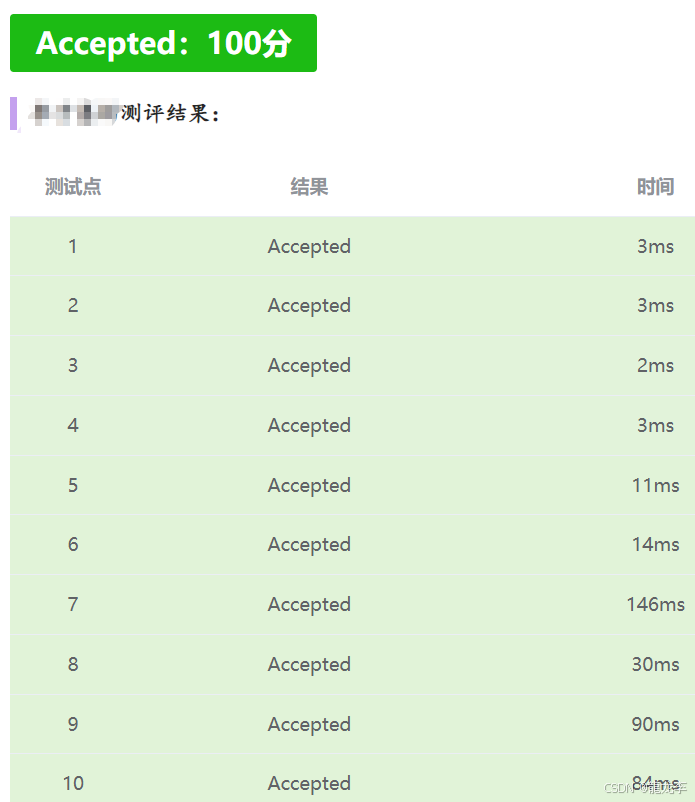
AC咯！