leetcode 111场双周赛 2023-8-19

博主是今年5月份开始刷leetcode的c语言小白，致力于周赛上分，csdn分享周赛的结果和题解。

与诸君共勉！

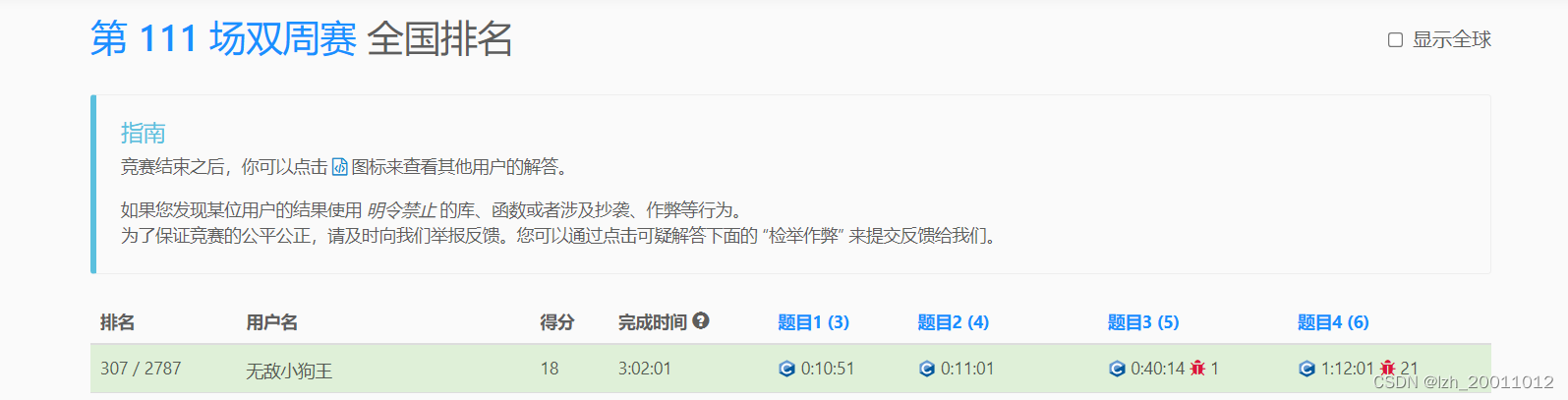
目前分数：

 本周赛成绩：

 周赛题解：

一，

 思路：

1，打卡题，遍历就可以

int countPairs(int* nums, int numsSize, int target){
    int res = 0;
    for(int i = 0;i<numsSize;i++)
    {
        for(int j = i+1;j<numsSize;j++)
        {
            if(nums[i]+nums[j] < target)
            {
                res++;
            }
        }
    }
    return res;
}

二，

        

 思路：

1，子序列，说白了就是从一个数组里面，按顺序拿自己喜欢的值组一个新数组

例如对于{1,2,3,4,5}数组,{1,3,5}就是他的一个子序列，但是{1，5，3}不是他的子序列，因为没有按顺序挑选

2，显然我只要在str1中按顺序遍历，只要str1[i] 通过 +0/+1变成str2，那就满足要求。

show show code

bool canMakeSubsequence(char * str1, char * str2){
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    int right1 = 0;
    int right2 = 0;
    int temp;
    while(right1 < len1 && right2 < len2)
    {
        temp = str2[right2] - str1[right1]   + 26;
        if(temp%26 <= 1)
        {
            right2++;
        }
        right1++;
    }
    if(right2 == len2)
    {
        return true;
    }
    return false;
}

三，

 思路：

1，这题可以转化一下，转化成为求数组的最长非递减子序列更容易理解。

int minimumOperations(int* nums, int numsSize){
    //找最长非递减子序列
    int dp[numsSize];
    for(int i = 0;i<numsSize;i++)
    {
        dp[i] = 0;
    }
	for(int i=0;i<numsSize;i++)
	{
		for(int j=0;j<i;j++)
		{
			if(nums[j]<=nums[i])
			dp[i]=fmax(dp[i],dp[j]+1);
		}
		
	}
	int m=dp[0];
	for(int i=0;i<numsSize;i++)
	{
		m=fmax(m,dp[i]);
	}
    return numsSize-m-1;
} 

2，做法原理。

对于一个数组来说[3,5,2,5,1,2,3,5,2,3,6,3]

假如要求最长非递减子序列需要考虑以下问题:

..........序列应该从哪开始..........遇到较大的数应不应该加入序列

看起来这问题比较麻烦

我们可以用dp来做，dp[i]为前i个数，最长序列长度。

序列每前进一位，我都从头更新一把dp。  dp[i] = dp[j] + 1 

j为i之前的数，且nums[i] >= nums[j]

复杂度N^2

四，

 这题思路很简单但是复杂度不好搞，在比赛中有两种想法。

1，从low到high遍历一把，满足num % k == 0 && fun(num) == true    fun()函数用来判断num是不是奇偶数位相同，但复杂度超了

2，从low开始找到第一个值，然后每次＋k,判断 fun(num+nk) == true即可，然后优化了一把，pass啦！

bool mmm(int a)
{
    int i = 0;//偶数
    int k = 0;//奇数
    int j = 0;
    while(a>0)
    {
        int temp = a%10;
        if(temp%2 == 0)
        {
            i++;
        }
        else
        {
            k++;
        }
        a /= 10;
    }
    return i==k;
}
int sss(int i)
{
    if(i >=1 && i<10)
    {
        return 10;
    }
    else if(i>=100 && i<1000)
    {
        return 1000;
    }
    else if(i>=10000 && i<100000)
    {
        return 100000;
    }
    else if(i>=1000000 && i<10000000)
    {
        return 10000000;
    }
    return i;
}
int numberOfBeautifulIntegers(int low, int high, int k){
    //先找到一个，然后每次+k
    int res = 0;
    int temp = 0;
    int flag = 0;
    low = sss(low);
    if(high > 99999999)
    {
        high = 99998888;
    }
    for(int i = low;i<=high;i++)
    {
        i = sss(i);
        if(i > high)
        {
            break;
        }
        if(i % k == 0)
        {
            if(mmm(i))
            {
                flag = 1;
                temp = i;
                break;
            }
        }
    }
    if(!flag)
    {
        return 0;
    }
    for(int i = temp;i<=high;i+=k)
    {
        if(mmm(i))
        {
            res++;
        }
    }
    return res;
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
}