Web GIS 地图投影与坐标系的研究与总结

坐标系问题一直是刚刚从事GIS行业的小伙伴们头疼的问题。有的同学是搞不清楚这些乱七八糟的坐标系，有的是搞懂了也不会操作，这篇文章就一次性带大家解决这个问题。

首先来思考这么一个问题：我们真实的地球是一个不规则的，赤道略宽，两极稍短的“扁”的椭球体。这个椭球体还是不规则的，曲折的，表面不平整的椭球体，真实的地球可能是：

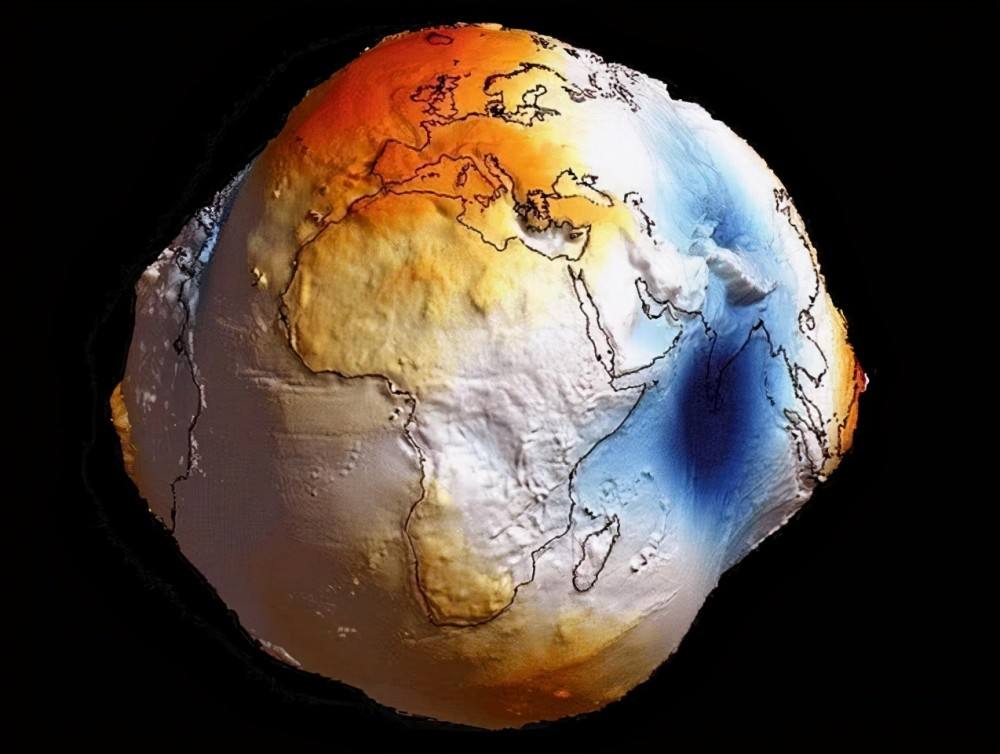
所以我们要在计算机，或者说数学的层面来精准的表达地球上的任意位置，就需要建立一套规则的空间几何系统。

因此呢科学家和地理学家就将地球呢抽象成了一个标准的椭球体。高中数学我们学习过椭圆，椭圆有长轴和短轴。实际上椭圆绕着一个固定的长度进行旋转就得到了椭球。

因此椭球肯定有三个关键要素：长轴a，短轴b，和旋转半径c。

在地球的实际测量中发现，长轴（也就是赤道半径），和旋转半径c是相等的。因为赤道处的半径几乎相等，赤道切面我们认为近似的是一个圆形。所以也就意味着地球椭球体只需要知道赤道半径和极半径即可描绘出一个椭球体。那么如何实时的调整并改变这个椭球体的形状呢？那就需要加上一个关键的参数：扁率。