A naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem (from Bayesian statistics) with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model".
In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature. For example, a fruit may be considered to be an apple if it is red, round, and about 4" in diameter. Even though these features depend on the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple.
Depending on the precise nature of the probability model, naive Bayes classifiers can be trained very efficiently in a supervised learning setting. In many practical applications, parameter estimation for naive Bayes models uses the method of maximum likelihood; in other words, one can work with the naive Bayes model without believing in Bayesian probability or using any Bayesian methods.
In spite of their naive design and apparently over-simplified assumptions, naive Bayes classifiers often work much better in many complex real-world situations than one might expect. Recently, careful analysis of the Bayesian classification problem has shown that there are some theoretical reasons for the apparently unreasonable efficacy of naive Bayes classifiers.[1] An advantage of the naive Bayes classifier is that it requires a small amount of training data to estimate the parameters (means and variances of the variables) necessary for classification. Because independent variables are assumed, only the variances of the variables for each class need to be determined and not the entire covariance matrix.
The naive Bayes probabilistic model
Abstractly, the probability model for a classifier is a conditional model
over a dependent class variable C with a small number of outcomes or classes, conditional on several feature variables F1 through Fn. The problem is that if the number of features n is large or when a feature can take on a large number of values, then basing such a model on probability tables is infeasible. We therefore reformulate the model to make it more tractable.
Using Bayes' theorem, we write
In plain English the above equation can be written as
In practice we are only interested in the numerator of that fraction, since the denominator does not depend on C and the values of the features Fi are given, so that the denominator is effectively constant. The numerator is equivalent to the joint probability model
which can be rewritten as follows, using repeated applications of the definition of conditional probability:
Now the "naive" conditional independence assumptions come into play: assume that each feature Fi is conditionally independent of every other feature Fj for 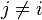 . This means that
. This means that
and so the joint model can be expressed as
This means that under the above independence assumptions, the conditional distribution over the class variable C can be expressed like this:
where Z is a scaling factor dependent only on 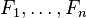 , i.e., a constant if the values of the feature variables are known.
, i.e., a constant if the values of the feature variables are known.
Models of this form are much more manageable, since they factor into a so-called class prior p(C) and independent probability distributions 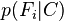 . If there are k classes and if a model for each
. If there are k classes and if a model for each 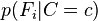 can be expressed in terms of r parameters, then the corresponding naive Bayes model has (k − 1) + n r k parameters. In practice, often k = 2 (binary classification) and r = 1 (Bernoulli variables as features) are common, and so the total number of parameters of the naive Bayes model is 2n + 1, where n is the number of binary features used for prediction.
can be expressed in terms of r parameters, then the corresponding naive Bayes model has (k − 1) + n r k parameters. In practice, often k = 2 (binary classification) and r = 1 (Bernoulli variables as features) are common, and so the total number of parameters of the naive Bayes model is 2n + 1, where n is the number of binary features used for prediction.




 朴素贝叶斯分类器是一种简单的概率分类器,基于应用贝叶斯定理,并假设特征间相互独立。该分类器认为每个特征独立地对类别概率做出贡献。尽管这种假设在现实中很少成立,但朴素贝叶斯分类器在许多复杂的真实世界情境中表现出意外的良好效果。
朴素贝叶斯分类器是一种简单的概率分类器,基于应用贝叶斯定理,并假设特征间相互独立。该分类器认为每个特征独立地对类别概率做出贡献。尽管这种假设在现实中很少成立,但朴素贝叶斯分类器在许多复杂的真实世界情境中表现出意外的良好效果。
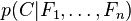
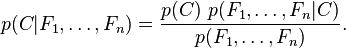


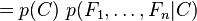

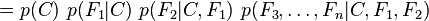

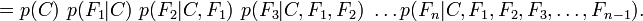
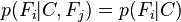
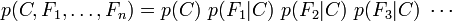
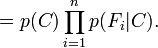
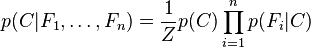
















 1338
1338

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








