第二章--线性表

线性表的基本概念

线性表是最简单、常用的线性结构（一个数据元素的有序关系）

定义：

具有相同特性的数据元素的一个有限序列。

一般表示为 （a1,a2...,ai-1,...,an）: a1是表头元素，an 是表尾元素， n 是线性表长度 (元素个数) n=0 表示线性表是一个空表，不包含任何元素， i 表示逻辑位序。

基本运算

InitList (&L): 初始化线性表  

DestroyList (&L)：销毁线性表

DispList (L)：输出线性表

ListEmpty (L)：判断线性表是否为空表

ListLength (L)：返回 L 中元素的个数

InitList (&L): 初始化线性表

DestroyList (&L)：销毁线性表

DispList (L)：输出线性表

ListEmpty (L)：判断线性表是否为空表

ListLength (L)：返回 L 中元素的个数

线性表的顺序存储结构

定义：

使用一块地址连续的存储空间，按照线性表中元素的逻辑顺序依次存放相应元素。

顺序线性表中第 i 个数据元素 ai的存储位置为：ai = a1(线性表的基地址) +（i-1）*len(每个元素的长度)。

顺序存储结构的特点：

1）逻辑相邻 <-> 物理地址相邻

2）实现随机存储（快速访问）。例：获取L中第i个元素的值，时间复杂度是O( 1 )。

顺序表的基本操作：

1、初始化顺序表，时间复杂度是O( 1 )

Status InitList(SqList &L){
    L.elem = new ElemType[MAXSIZE];// 分配MAXSIZE大小的空间
    if (!L.elem) exit(OVERFLOW);  // 存储分配失败, 退出
    L.length = 0;
    return OK;
}

2、销毁线性表，时间复杂度是O( 1 )

void DestroyList(SqList &L){
    delete[] L.elem;
    L.elem = nullptr;
    L.length = 0;
}

3、输出线性表，时间复杂度是O( Length(L) )

void DispList(SqList L){
    for(int i = 0; i < L.length; i++)
        cout << L.elem[i];
    cout << endl;
}

4、获取L中第 i 个元素，时间复杂度是O( 1 )

Status GetElem(SqList L, int i, ElemType& e){
    if (i < 1 || i > L.length)
        return ERROR;
    e = L.elem[i-1];
    return OK;
}

5、按元素值查找

int LocateElem(SqList L, ElemType e){
    for(int i = 0; i < L.length; i++)
        if (L.elem[i] == e)
            return i+1; // 返回元素的逻辑位序
    return 0;          // 查找失败, 返回0
}

6、插入

要在第 i 个位置插入e，须将 i 到 n 之间的元素往后移，时间复杂度是O( n )。

Status ListInsert(SqList L, int i, ElemType e){
    if (i < 1 || i > (L.length+1))
        return ERROR;            // 删除位置不合法
    if (L.length == MAXSIZE)
        return ERROR;            // 存储空间已满
    i--;                         // 将顺序表逻辑序号转化为物理序号
    for(int j = L.length; j > i; j--) // 将elem[i..n]元素后移
        L.elem[j] = L.elem[j-1];
    L.elem[i] = e;               // 在i位置插入元素e
    L.length++;                  // 顺序表长度增1
    return OK;
}

插入元素算法时间复杂度的讨论：

1）插入位置从 1 到 n+1，在每个位置插入的概率为 1/(n+1) 。

2）在位置 n+1 插入，移动 0 次 ；在位置 1 插入，移动 n 次。

移动次数的期望值如下述公式：

 7、删除

要将第 i 个位置的元素删除，需将位置为 i+1 到 n 的元素往前移，时间复杂度是O( n )。

Status ListDelete(SqList L, int i, ElemType& e){
    if (i<1 || i>L.length) // 删除位置不合法
        return false;
    i--;                    // 将顺序表逻辑序号转化为物理序号
    e = L.elem[i];
    for(int j=i; j<L.length-1; j++)//将elem[i..n-1]元素前移
        L.elem[j] = L.elem[j+1];
    L.length--;             // 顺序表长度减1
    return OK;
}

 删除元素时间复杂度的讨论

1）删除位置从 1 到 n，在每个位置删除的概率为 1/n 。

2）在位置 n 删除，移动 0 次 在位置 1 删除，移动 n - 1 次 。

移动次数的期望值如下述公式：

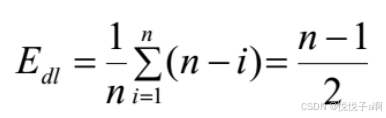
线性表的链式结构

定义：

线性表中的数据元素存放在一组地址任意的存储节点，节点之间使用指针进行连接 。与顺序表不同，链表无需连续的存储空间。

typedef struct LNode   // 定义单链表节点结构体
{
    ElemType data;     // 数据域
    struct LNode *next; // 指向后继节点
} LNode, *LinkList;

结构节点 = 数据元素 + 指针。

数据元素：存放数据。

指针：存放该节点下一个元素的存储位置。

头指针：表头指针（head）指向链表的第一个节点。

头节点：简化插入与删除的操作。

存储密度 = 数据所占空间 / 节点所占用空间（数据占用空间 + 指针占用空间）

链表的存储密度不高，比起顺序表来说存储空间的利用率较低。

链表的基本操作：

1、初始化单链表 InitList (L)

Status InitList(LinkList &L) // LinkList 等于 LNode*
{
    L = new LNode;//创建头节点
    L->next = NULL;
    return OK;
}

2、销毁线性表 DestroyList (L)

Status DestroyList(LinkList L)
{
    LNode *p;
    while(L->next) {
        p = L->next;
        L->next = p->next;
        delete p;
    }
}

 3、判断线性表是否为空表 ListEmpty (L)

bool ListEmpty(LinkList L){
    return (L->next == NULL);
}

4、求线性表的长度 ListLength (L)

int ListLength(LinkList L)
{ int n=0;
    LinkList p = L;   //p指向头节点, n置为0(即头节点的序号为0)
    while(p->next != NULL)
    {  n++;
        p=p->next;
    }
    return n;        //循环结束, p指向尾节点, 其序号n为节点个数
}

5、输出线性表 DispList (L)

void DispList(LinkList L) {
    LinkList p = L->next;  // 从首元节点开始，头节点一般不存储有效数据
    while (p != NULL) {
        // 输出当前节点的数据域，这里假设ElemType类型可以直接用cout输出
        // 如果是自定义类型，可能需要重载<<运算符
        std::cout << p->data << " "; 
        p = p->next;
    }
    std::cout << std::endl;
}

6、求线性表 L 中指定位置的某个数据元素，时间复杂度为O( ListLength(L) )

bool GetElem(LinkList L, int i, ElemType &e)
{ int j=0;
    LinkList p = L;   // p指向头节点,j置为0(即头节点的序号为0)
    while (j<i && p!=NULL){ j++; p=p->next;} // 什么时候退出循环?
    if (p == NULL)     // 不存在第i个数据节点,返回false
        return false;
    else                // 存在第i个数据节点,返回true
    {  e = p->data;
        return true;
    }
}

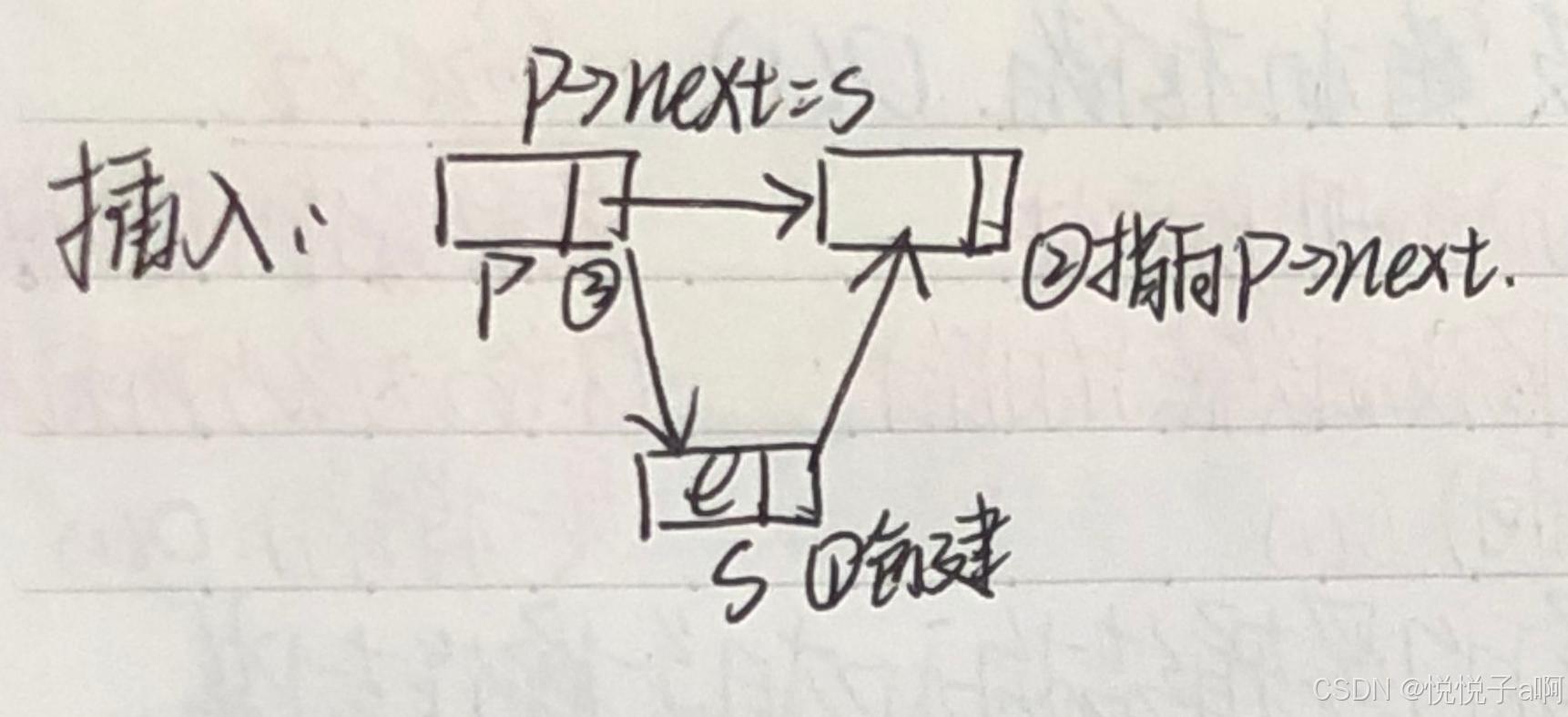
7、插入数据元素 ListInsert (L, i, e)，时间复杂度为O( ListLength(L) )

bool ListInsert(LinkList L, int i, ElemType e) {
    int j = 0;
    LinkList p = L; 
    while (j < i - 1 && p != NULL) {
        j++;
        p = p->next;
    }//找到这个元素的位置
    if (p == NULL) 
        return false; 
    else {
        LNode* s = new LNode; 
        s->data = e; 
        s->next = p->next; 
        p->next = s; 
        return true;
    }
}

8、删除数据元素 ListDelete (L, i, &e)，时间复杂度为O( ListLength(L) )

bool ListDelete(LinkList L, int i, ElemType &e)
{ int j=0;
    LinkList p = L, *q;        //p指向头节点, j置为0
    while (j<i-1 && p!=NULL)   //查找第i-1个节点
    {  j++;
        p = p->next;
    }
    if (p == NULL)             // 未找到第i-1个节点,返回false
        return false;
    else
    {  q = p->next;           // q指向第i个节点
        if (q == NULL)         // 若不存在第i个节点,返回false
            return false;
        e = q->data;
        p->next = q->next; // 从单链表中删除*q节点
        delete q;           // 释放*q节点
        return true;        // 返回true表示成功删除第i个节点
    }
}

9、建立单链表 - 头插法

思路：生成一个空表，不断将新节点插入链表表头。

void CreateListF(LinkList& L, ElemType a[], int n)
{ LinkList s;
    int i;
    L = new LNode;        // 对L进行赋值，因此应使用引用类型参数
    L->next = NULL;      // 创建头节点,其next域置为NULL
    for (i=0; i<n; i++){  // 循环建立数据节点
        s = new LNode;
        s->data = a[i];  // 创建数据节点*s
        s->next = L->next; // 将*s插在原开始节点之前,头节点之后
        L->next = s;
    }
}

 10、建立单链表 - 尾插法（链表节点的顺序与逻辑次序相同）

思路：将新节点始终插入链表表尾，需要一个尾指针 r。

void CreateListR(LinkList& L, ElemType a[], int n)
{ LinkList *s,*r;
    int i;
    L = new LNode;          // 创建头节点
    r = L;                  // r始终指向尾节点,开始时指向头节点
    for (i = 0; i < n; i++) // 循环建立数据节点
    {  s = new LNode;
        s->data = a[i];    // 创建数据节点*s
        r->next = s;       // 将*s插入*r之后
        r = s;
    }
    r->next = NULL;        // 尾节点next域置为NULL
}

11、循环链表（拓展）

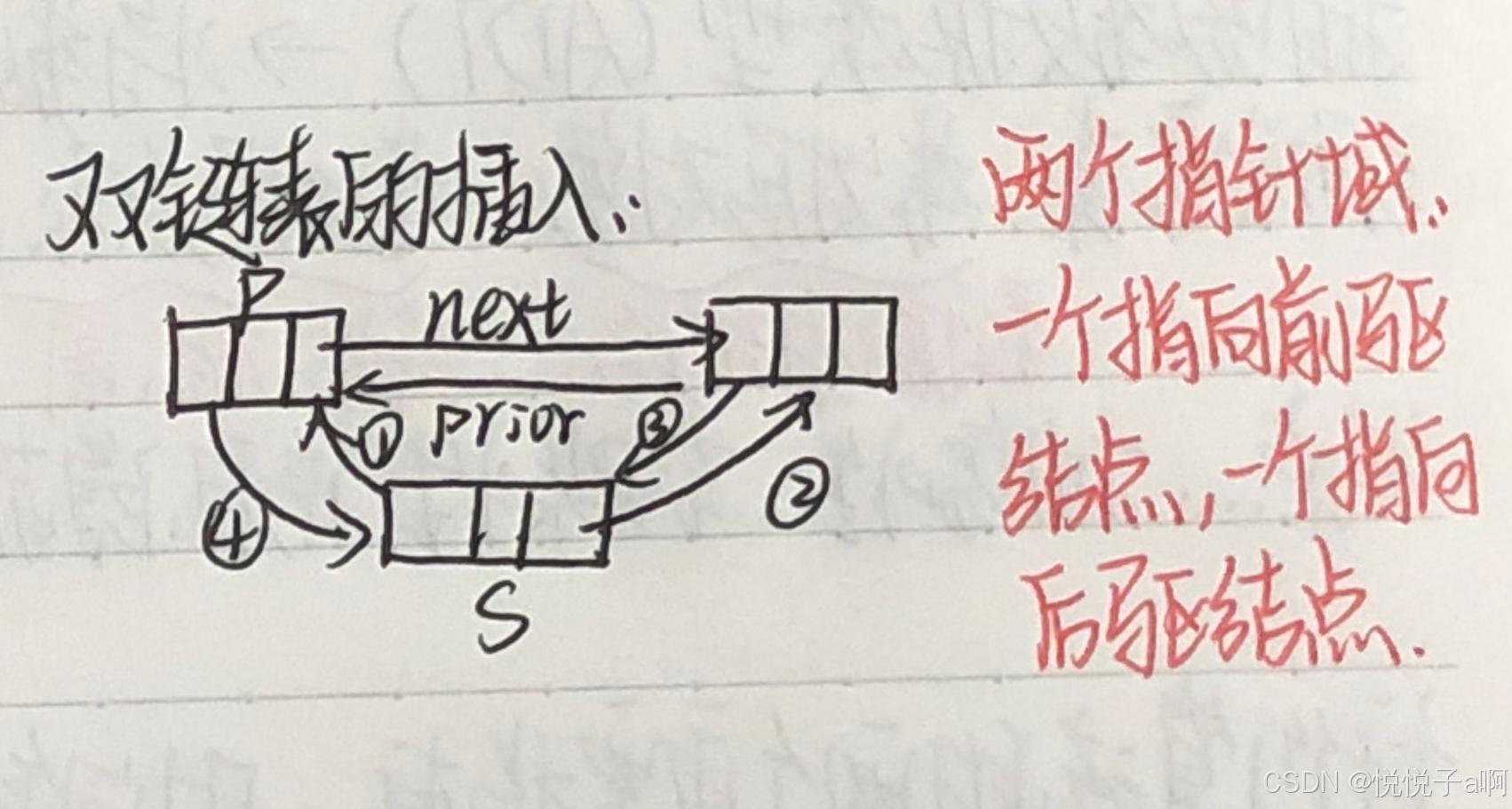
 12、双链表（拓展）

两种存储结构的比较：

链表在插入和删除操作上相对顺序表更灵活高效，不需要移动大量元素，只需修改指针指向；但在随机访问元素时，效率比顺序表低。

线性表的应用

1、一元多项式的存储

1）数组存储：对于一元多项式，可以用数组来存储系数。这种方式简单直观，对于幂次连续且多项式不太稀疏的情况比较适用。但如果多项式稀疏（很多项系数为 0 ），会浪费大量存储空间。

2）链表存储：采用链表结构，每个节点存储多项式的一项信息，包括系数和指数，只存储非零项，能有效节省存储空间，适用于稀疏多项式。

节点结构可以定义为：

typedef struct PolyNode {
    float coef;  // 系数
    int expn;    // 指数
    struct PolyNode *next;
} PolyNode, *Polynomial;

3）哈希表辅助（散列表）：在某些场景下，对于非常大规模且幂次分布复杂的稀疏多项式，可以结合哈希表来存储。哈希表有一个哈希函数 (h(key)) ，它将输入的键（指数 ）转换为一个整数，这个整数作为在哈希表数组中的索引，对应的值（系数 ）就存储在该索引位置。通过哈希函数计算键对应的索引，将系数存储到哈希表相应位置。

 

有序表

1、有序表的插入：为了保持表中元素有序，在有序表中插入与在普通线性表中插入操作不一样。

2、有序顺序表的插入

void ListInsert(SqList L, ElemType e)
{ int i=0, j;
    while (i<L.length && L.data[i]<e)
        i++;                          // 查找大于e的下标i
    for(j = L.length; j > i; j--)     // 从后往前
        L.elem[j] = L.elem[j-1];      // 将elem[i..n]后移一个位置
    L.elem[i] = e;
    L.length++;                       //有序顺序表长度增1
}

3、有序链式表的插入

void ListInsert(LinkList L, ElemType e)//LinkList == LNode*
{
    LinkList pre = L, *p;
    while (pre->next != NULL && pre->next->data<e)
        pre = pre->next;      //查找插入节点的前驱节点*pre
    p = new LNode;
    p->data = e;             //创建存放e的数据节点*p
    p->next = pre->next;    //在*pre节点之后插入*p节点
    pre->next = p;
}