绪论--数据结构与算法基础

数据结构的定义

数据结构是计算机科学中用于组织、存储和管理数据的一种方式，它不仅描述了数据的存储形式，还定义了数据之间的关系以及可以对数据执行的操作。

逻辑结构

指数据元素之间的逻辑关系，主要有以下几种类型：

1、集合结构：数据元素属于同一个集合，元素之间除了同属于一个集合外，没有其他特殊关系。

2、线性表：节点之间关系：一对一。如数组、链表、栈、队列等。

3、树：节点之间关系：一对多。如二叉树、多叉树等。

4、图：节点之间关系：多对多。图中的每个顶点都可以与多个其他顶点相关联。

存储结构

是数据结构在计算机中的表示，即数据的物理存储方式，主要有以下两种：

1、顺序存储结构：把数据元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的。比如数组就是典型的顺序存储结构。

2、链式存储结构：把数据元素存放在任意的存储单元里，这些存储单元可以是连续的，也可以是不连续的。通过指针来表示数据元素之间的逻辑关系，像链表就是链式存储结构。

操作

定义了一系列针对数据结构的操作，如插入、删除、查找、遍历、排序等。这些操作是对数据结构进行处理和维护的基本手段，不同的数据结构针对这些操作有不同的实现方式和时间复杂度。

逻辑结构的描述

1、逻辑结构包括两个方面：

1）数据元素的集合D；

2）D上的关系集合R，即数据元素之间的关系集合；

2、用二元组描述（序偶x,y）

注：rj 表示集合R中的第 j 个关系，每个关系用序偶表示。 序偶 <x,y>（x,y∈D） x 为第 1 个元素，y 为第 2 个元素。

存储结构类型

数据的逻辑结构：在计算机中的存储形式。

逻辑结构->映射->存储结构

存储时应包含两个方面内容：数据元素、数据元素之间的逻辑关系。

两种基本的存储结构

1、顺序存储结构：

逻辑上相邻存储在物理位置上相邻的存储单元，如 C 语言中的数组，char arr [26] 。

2、链式存储结构：

各个节点地址不连续，通过指针体现数据元素之间的逻辑关系。

逻辑结构与存储结构的关系

1、存储结构是逻辑结构在计算机中的存储形式。

2、同一逻辑结构可以对应多种存储结构。

3、同样的操作在不同的存储结构上，实现方法不同。

数据基本概念的定义

1、数据元素：数据结构中讨论的基本单位。
2、数据项：数据结构中讨论的最小单位。

数据类型

一组性质相同的值的集合、及定义在此集合上的一组操作的总称。

1、是高级程序设计语言中的一个基本概念。

2、顺序存储或链式存储结果，可以借助程序语言中的数组、指针来实现。

例：

C语言中的 int 数据类型。其数值范围是 -32768~32767 ；操作集合就是 +、-、*、/、%等等。

抽象数据类型（ADT）

1、用户定义的、表示应用问题的数学模型以及定义在该模型上的一组操作的总称。

2、包含：数据对象、关系集合、基本操作。

例：

ADT Complex {

数据对象（数据元素的集合）：

D={ e1 ，e2 | e1 ，e2 均为实数}

数据关系（线性、树、图）：

 R={ < e1 , e2 > | e1 是复数的实数部分，e2 是复数的虚数部分 }

基本操作（插入、删除、查找、排序）:

AssignComplex (&z ，v1 ，v2)： 构造复数 z 

GetReal (z ，&real)：返回复数 z 的实部值

GetImag (z ，& Imag)： 返回复数 z 的虚部值

......

} ADT Complex

算法

算法是为解决特定问题而设计的一系列有序指令集合，这些指令明确了从输入到输出的操作流程。比如计算两个数相加，通过加法指令将输入的两个数进行运算得出结果，这一系列的操作步骤就是算法。

特性

1、有穷性：算法不能无限循环执行下去，必须在有限的步骤后结束。

2、确定性：算法的每一步都有明确、唯一的含义，不会产生歧义。

3、可行性：算法中的操作都能够通过计算机已有的基本运算（如加、减、乘、除等）在有限次内实现。（计算一个数的平方根，虽然不是直接的基本运算，但可以通过迭代等有限次基本运算来近似实现）。

输入：算法运行前需要处理的数据对象，可以没有输入，也可以有多个输入。

输出：算法执行完成后必须要有结果输出，至少一个。

算法的描述

（例子都以欧几里得算法--辗转相除法求两个自然数 m 和 n 的最大公约数为例）

1、自然语言

2、流程图

3、程序设计语言（譬如C语言）

4、伪代码（是一种介于自然语言和程序设计语言之间的方法，采用某一程序设计语言的基本语法，结合自然语言的操作指令来设计算法）

算法的分析

1、正确性：这是算法最基本的要求。算法必须能按照预期准确执行规定功能。

2、可使用性：算法应方便用户操作和调用。

3、可读性：算法的代码或描述应易于理解、可读性好。

4、健壮性：算法要具备容错能力。当输入异常数据，如在计算除法时输入除数为 0，算法不能崩溃，而应能给出提示信息或进行合理处理，避免程序异常终止。

5、时间效率高与存储量低：时间效率高指算法执行速度快，能在较短时间内得出结果；存储量低则是算法在运行过程中占用的存储空间少。

算法的时间复杂度和空间复杂度

时间复杂度是用来度量算法执行时间的一个概念，它表示算法执行基本操作的次数与问题规模之间的关系（操作次数随数据输入量增大的增长趋势）。这里的问题规模通常是指输入数据的数量，比如对数组排序，数组元素个数就是问题规模。

表示方法：

一般用大O记号来表示，记作O( f ( n ))，其中，n 是问题规模， f ( n ) 是一个关于 n 的函数。

常见类型：

常数阶 O(1) ：算法的执行时间不随输入规模增加而变化。比如从数组中取第一个元素，操作次数始终为 1 ，时间复杂度是 O(1) 。

线性阶 O(n)：基本操作次数与问题规模 n 成正比，如遍历数组求和。

对数阶 O( log n )：常见于二分查找等算法，随着 n 增大，操作次数增长缓慢。

平方阶 O( n^2 )：如冒泡排序，对 n 个元素排序，比较操作次数接近 n^2 。

函数图像大概是这样：

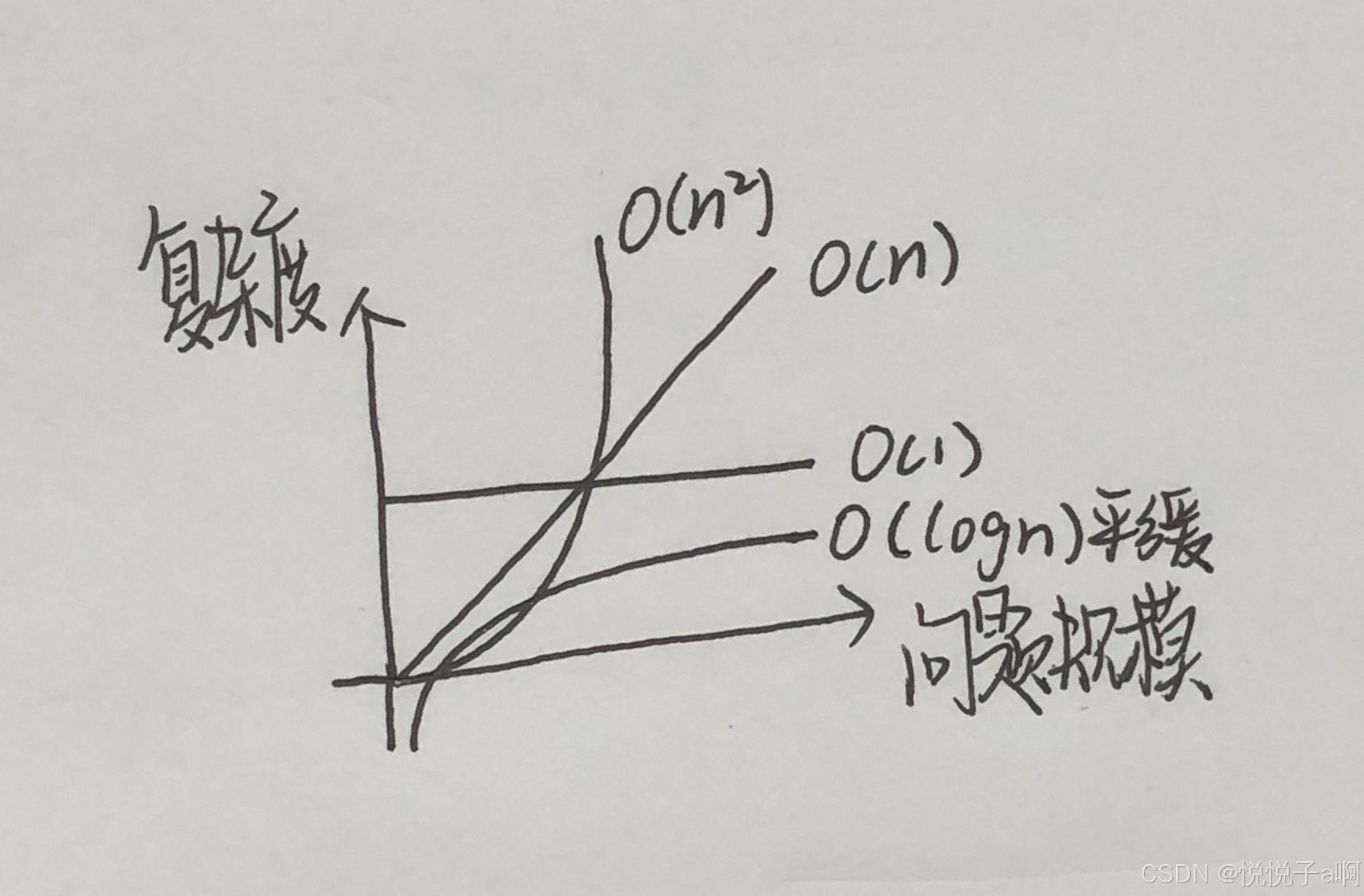
从图像上看：O(1) 和 O( log n ) 较为平缓，是理想的时间复杂度类型。

计算方法：

1、确定基本操作，找出算法中执行次数最多的操作。

2、建立基本操作执行次数与输入规模 n 之间的关系式。

3、只看最高阶。

总结就是：主要看内层循环、最高阶。

空间复杂度是对算法运行过程中临时占用存储空间大小的量化度量。它反映了随着问题规模 n 变化，算法临时占用空间的增长趋势。

表示方法：

一般用 S(n) = O(g(n)) 表示，其中 n 是问题规模，g (1)  是关于 n 的函数。例如，若算法在运行时，临时创建一个长度为 n 的数组，那么空间复杂度就是O(n) ；若临时占用空间固定，不随 n 变化，如只使用一个临时变量，空间复杂度就是 O(1)  。

通常情况下，鉴于运算空间较为充足，常以算法的时间复杂度作为算法优劣的衡量指标。