R语言时间序列学习+代码记录5：Modeling Seasonal ARIMA

本文链接：https://blog.youkuaiyun.com/lxyhehehehe/article/details/143366111

一、背景和原理：

1.ARIMA模型（自回归积分滑动平均模型）

适用于有明显趋势、季节性或自相关特征的数据。ARIMA模型能有效处理非平稳时间序列，综合了自回归（AR）、差分（I）和移动平均（MA）三部分，捕捉了序列中的滞后关系和随机波动。

（1）组成部分

AR (自回归)部分：表示当前值与过去一段时间内的值之间的关系，使用滞后项描述。假设AR部分的阶数为p，则模型可以表示为：

$y_t = c + \phi_1 y_{t-1} + \phi_2 y_{t-2} + \dots + \phi_p y_{t-p} + \epsilon_t$
其中 $\phi_i$ 为自回归系数， $y_{t-i}$ 为滞后项，c为常数项， $\epsilon_t$ 是白噪声项。

I (差分)部分：通过对序列进行差分处理，将非平稳的序列转化为平稳序列。差分的阶数d表示序列需要被差分的次数，以使其变得平稳。一次差分表示 $y_t - y_{t-1}$ ，若d=1，表示对序列进行一次差分。
MA (移动平均)部分：表示当前值与过去白噪声项的线性组合关系。假设MA部分的阶数为q，则模型可以表示为：

$y_t = c + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \dots + \theta_q \epsilon_{t-q}$
其中 $\theta_i$ 为移动平均系数， $\epsilon_t$ 为当前时刻的随机误差项， $\epsilon_{t-i}$ 为滞后误差项。

（2）ARIMA模型表示与构建方法

模型用ARIMA(p, d, q)来表示，其中：

p：AR部分的阶数，即自回归项的滞后阶数
d：I部分的阶数，即差分次数
q：MA部分的阶数，即移动平均项的滞后阶数

例如，ARIMA(1, 1, 1)模型表示差分一次后，包含一个滞后自回归项和一个滞后移动平均项。

一般来说，如果ACF在某个滞后阶数q之后迅速衰减，说明适合MA(q)模型；如果PACF在某个滞后阶数p之后迅速衰减，说明适合AR(p)模型。

2.季节性 ARIMA 模型（SARIMA，Seasonal ARIMA）

对ARIMA模型的一种扩展，用于捕捉时间序列中的季节性特征。SARIMA模型在基本ARIMA模型的基础上增加了季节性参数，以便更准确地描述带有周期性波动的序列，比如季度销售额、月度温度变化等具有明显季节性规律的数据。

（1）表示方式

SARIMA模型通常记为 SARIMA(p, d, q) × (P, D, Q, s)，其中：

(p, d, q)：表示原序列的非季节性ARIMA部分参数
- p：非季节性自回归（AR）项的阶数
- d：非季节性差分次数
- q：非季节性移动平均（MA）项的阶数
(P, D, Q, s)：表示季节性ARIMA部分的参数
- P：季节性自回归（SAR）项的阶数
- D：季节性差分次数
- Q：季节性移动平均（SMA）项的阶数
- s：季节周期的长度（如季度数据s=4，月度数据s=12）

这些参数的含义与ARIMA模型中的参数相似，但应用在季节性周期上。季节性周期s是时间序列数据中周期性重复的间隔。

（2）数学形式

基本公式为：

$\Phi_P(B^s)(1 - B^s)^D (1 - B)^d y_t = \Theta_Q(B^s) \theta_q(B) \epsilon_t$

其中：

B：表示滞后算子，即 $B^k y_t = y_{t-k}$
$\Phi_P(B^s)$ ：季节性自回归项，包含P个季节性滞后项
$(1 - B^s)^D$ ：季节性差分运算，差分次数为D
$\Theta_Q(B^s)$ ：季节性移动平均项，包含Q个季节性滞后误差项
$\theta_q(B)$ ：非季节性移动平均项，包含q个非季节性滞后误差项
$\epsilon_t$ ：白噪声项

（3）组成部分

SARIMA模型结合了非季节性和季节性的三个主要部分：

1. 非季节性部分（ARIMA模型的常规部分）：

AR(p)：非季节性自回归项，描述当前值与前p期值之间的关系
I(d)：非季节性差分项，用于平稳化序列
MA(q)：非季节性移动平均项，描述当前值与前q期随机误差之间的关系

2. 季节性部分：

SAR(P)：季节性自回归项，描述当前值与前 $P \times s$ 期值之间的关系
SI(D)：季节性差分项，用于消除季节性波动
SMA(Q)：季节性移动平均项，描述当前值与前 $Q \times s$ 期随机误差之间的关系

3. 季节周期 (s)：代表季节周期的长度。

2.背景与数据

（1）问题背景

Traveler's Rest, Inc.在美国中西部城市经营着四家酒店。要求该公司运营部门的分析人员开发一个模型，用于获得短期预测（最多一年）酒店入住房间数的预测。各种人员需要这些预测来协助决策在夏季雇佣额外的帮手、订购交货期较长的材料，编制本地广告支出预算、本地广告支出等。可用的历史数据包括前一时期每天入住的房间数。由于希望获得月度预测，这些数据将每个月的总数除以该月的月的天数。15 年中前 14 年的月平均客房数，分别用 y1、y2、......、y168 表示。

（2）数据与基础设置：

501
488
504
578
545
632
728
725
585
[1:168]

s <- 12 # 月度数据
startyear <- 1
h <- 12  # 预测长度12
T <- length(data) 
years <- T/s 
data <- ts(data, start=c(startyear,1),frequency=s);plot(data)
y<-log(data); plot(y)

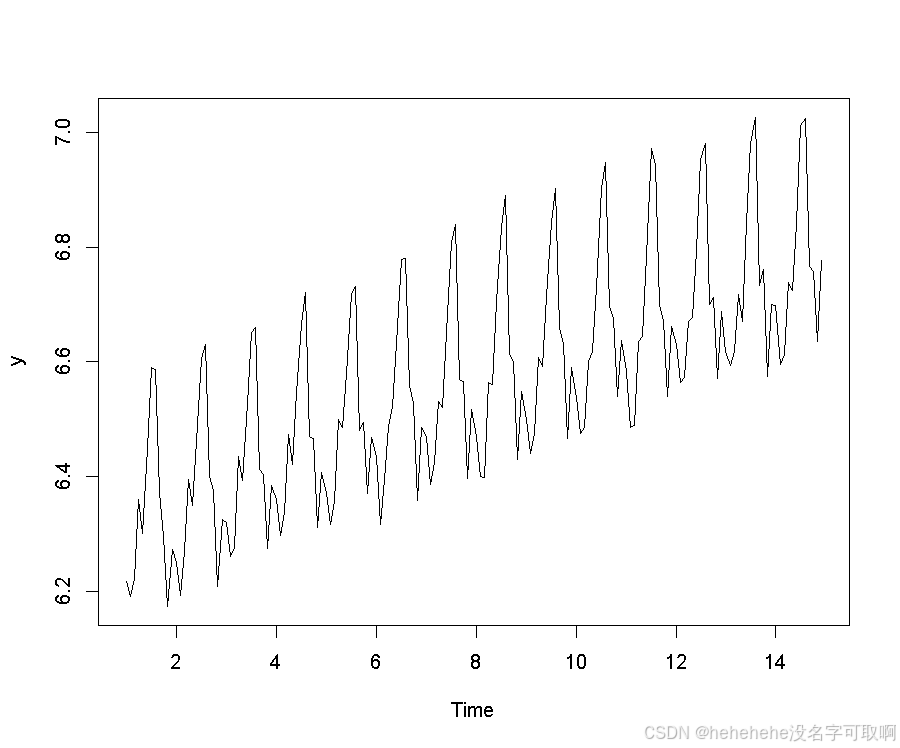
二、处理季节性成分

1.去除季节性

yy <- diff(y,lag=s)# 进行季节性差分,去除季节性成分
plot(yy)

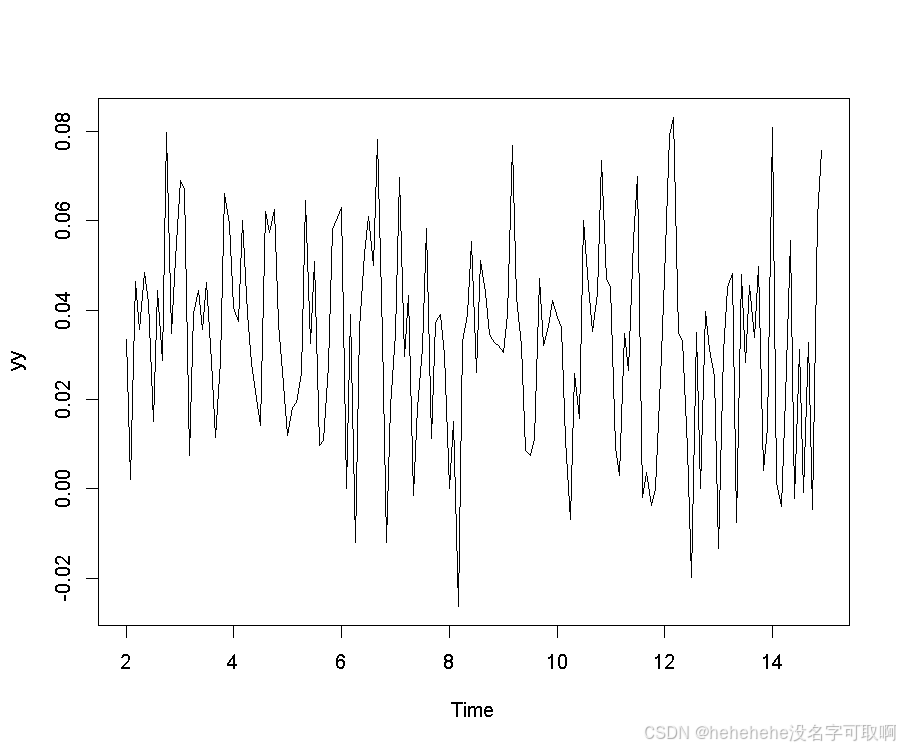
2.检验

（1）单位根检验

test <- ur.df(yy,type=c("drift"),lags=10,selectlags="AIC")
summary(test)
# type=c("drift") - 包含漂移项，lags=10 - 滞后阶数为10

Test regression drift 
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
Residuals:
      Min        1Q    Median        3Q       Max 
-0.051719 -0.014374  0.001257  0.014357  0.059142 
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.035948   0.006835   5.259 5.38e-07 ***
z.lag.1     -1.095914   0.201090  -5.450 2.25e-07 ***
z.diff.lag1  0.326930   0.170732   1.915   0.0576 .  
z.diff.lag2  0.303874   0.151253   2.009   0.0465 *  
z.diff.lag3  0.100141   0.127258   0.787   0.4327    
z.diff.lag4  0.087875   0.108314   0.811   0.4186    
z.diff.lag5 -0.157806   0.085312  -1.850   0.0665 .  
---
Residual standard error: 0.02176 on 138 degrees of freedom
Multiple R-squared:  0.4683,	Adjusted R-squared:  0.4452 
F-statistic: 20.26 on 6 and 138 DF,  p-value: < 2.2e-16
Value of test-statistic is: -5.4499 14.8507 
Critical values for test statistics: 
      1pct  5pct 10pct
tau2 -3.46 -2.88 -2.57
phi1  6.52  4.63  3.81

结果显示，tau统计量（-5.4499）小于临界值（-3.46），可以拒绝单位根假设，认为差分后的时间序列yy是平稳的。

（2）可视化对比原始数据、对数转换、季节性差分数据

par(mfrow=c(3,1), mar=c(3,5,3,3)) 
plot(data, main="Hotel occupancy rate")
plot(y, main="Hotel occupancy rate, log-transformed")
plot(yy, main="Hotel occupancy rate, after seasonal differencing")
dev.off()

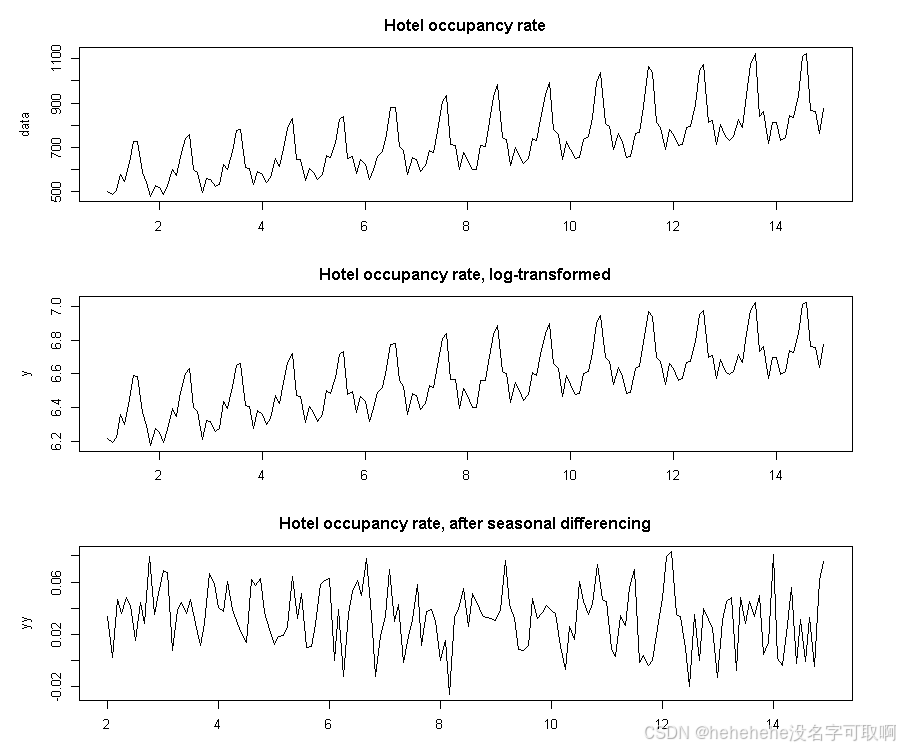
（3）季节性差分后数据ACF，PACF分析

par(mfrow=c(2,1), mar=c(3,5,3,3)) 
acf(yy, lag.max = 3*s); pacf(yy, lag.max = 3*s)
dev.off()
# lag.max = 3*s - 最大滞后阶数为3年的季节性周期（36个月）

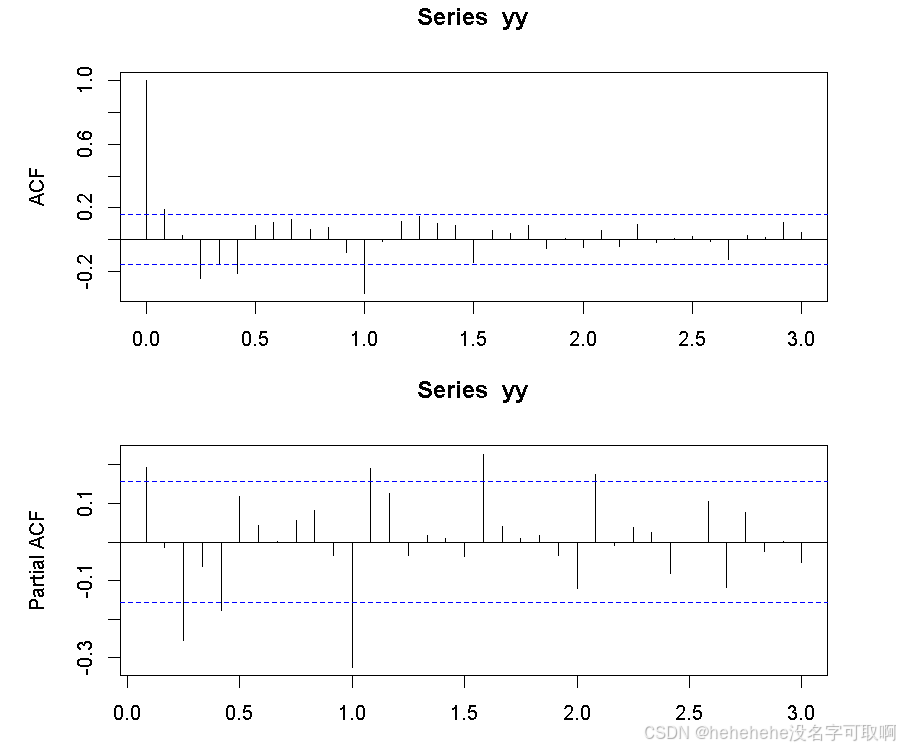
三、构建季节性ARIMA模型

1.ARIMA(3,0,0)(0,1,1)[12]模型构建

自动选择模型：

model.arima <- auto.arima(y, d=0, seasonal = TRUE, ic = "aic", 
                          stepwise = FALSE, approximation = FALSE, 
                          trace = TRUE)
# d=0 - 不进行差分，因为已经进行了季节性差分。
# seasonal = TRUE - 指定为季节性模型。

结果：Best model: ARIMA(3,0,0)(0,1,1)[12] with drift，根据结果构建模型

model.sar3 <- Arima(y,order = c(3, 0, 0),seasonal = c(0,1,1))#use Arima for the accuracy function
model.sar3 <- arima(y,order = c(3, 0, 0),seasonal = c(0,1,1))#use arima to get table of results
screenreg(model.sar3)

模型参数估计结果：

===========================
ar1                0.57 ***
                  (0.08)   
ar2                0.39 ***
                  (0.09)   
ar3                0.02    
                  (0.08)   
sma1              -0.66 ***
                  (0.08)   
---------------------------
AIC             -726.62    
BIC             -711.37    
Log Likelihood   368.31    
Num. obs.        156       
===========================

2.模型残差ACF,PACF分析

par(mfrow=c(2,1), mar=c(3,5,3,3)) 
acf(model.sar3$residuals); pacf(model.sar3$residuals)
dev.off()

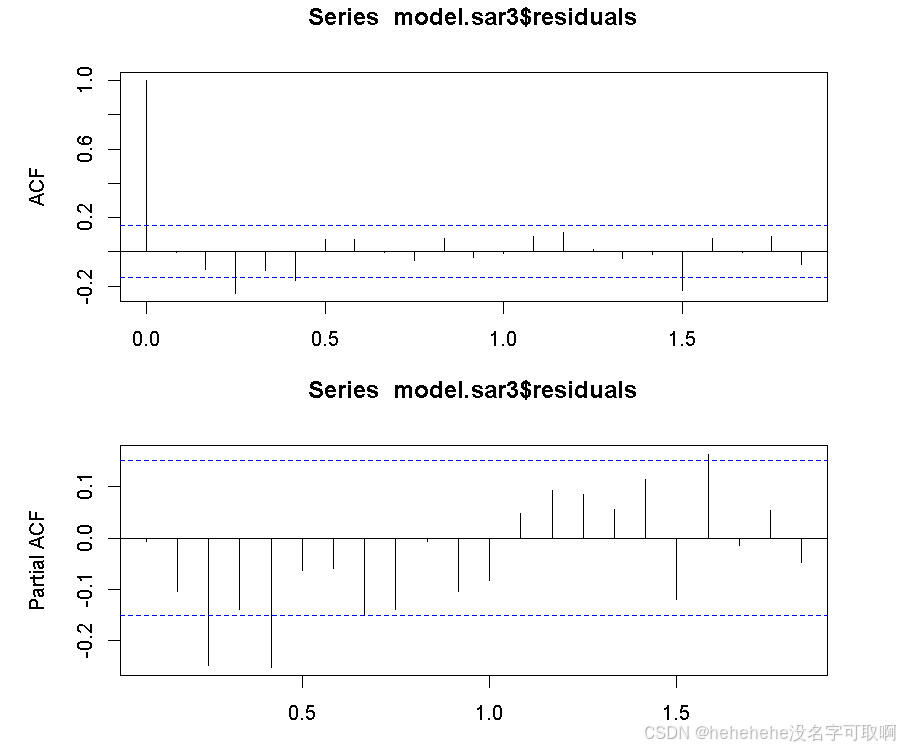
3.生成预测结果

SAR3.Forecast<-forecast(model.sar3, h=h)
SAR3.Forecast

Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 15       6.730094 6.701626 6.758562 6.686555 6.773633
Feb 15       6.660232 6.627462 6.693002 6.610114 6.710350
Mar 15       6.675276 6.636692 6.713861 6.616267 6.734286
Apr 15       6.792096 6.749258 6.834934 6.726581 6.857611
May 15       6.777173 6.730335 6.824011 6.705541 6.848805
Jun 15       6.908531 6.858159 6.958904 6.831493 6.985569
Jul 15       7.066338 7.012712 7.119964 6.984324 7.148351
Aug 15       7.088824 7.032206 7.145443 7.002233 7.175415
Sep 15       6.820870 6.761469 6.880271 6.730024 6.911717
Oct 15       6.818360 6.756360 6.880360 6.723539 6.913181
Nov 15       6.671213 6.606773 6.735653 6.572660 6.769765
Dec 15       6.796238 6.729499 6.862977 6.694169 6.898306

四、构建带有趋势和季节性成分（TSC）的模型

1.生成季节性虚拟变量

t = (1:T)
M <- seasonaldummy(y) # 生成季节性虚拟变量矩阵M
TrSeasL <- model.matrix(~ t + M) # 创建包含时间趋势t和季节性虚拟变量M的设计矩阵TrSeasL

model.arma <- auto.arima(y, d=0, seasonal = FALSE, ic = "aic", xreg=TrSeasL, 
                         stepwise = FALSE, approximation = FALSE, 
                         trace = TRUE)
# 自动选择模型中，外生回归变量 xreg=TrSeasL 包含时间趋势和季节性成分

结果显示，Best model: Regression with ARIMA(3,0,0) errors，故应构建包含时间趋势和季节性成分的AR(3)模型。

2.构建包含时间趋势和季节性成分的AR(3)模型

model.ar3 <- arima(y, order = c(3, 0, 0), include.mean = FALSE, xreg=TrSeasL)
# 显示 model.ar3 和 model.sar3 的参数估计结果
screenreg(list(model.ar3, model.sar3))
# 使用 Arima 函数创建相同的模型，用于后续预测
model.ar3 <- Arima(y, order = c(3, 0, 0), include.mean = FALSE, xreg=TrSeasL)

========================================
                Model 1      Model 2    
----------------------------------------
ar1                0.39 ***     0.57 ***
                  (0.08)       (0.08)   
ar2                0.19 *       0.39 ***
                  (0.08)       (0.09)   
ar3               -0.26 ***     0.02    
                  (0.08)       (0.08)   
(Intercept)        6.29 ***             
                  (0.01)                
t                  0.00 ***             
                  (0.00)                
MJan              -0.04 ***             
                  (0.01)                
MFeb              -0.11 ***             
                  (0.01)                
MMar              -0.08 ***             
                  (0.01)                
MApr               0.04 ***             
                  (0.01)                
MMay               0.02 **              
                  (0.01)                
MJun               0.15 ***             
                  (0.01)                
MJul               0.29 ***             
                  (0.01)                
MAug               0.31 ***             
                  (0.01)                
MSep               0.06 ***             
                  (0.01)                
MOct               0.04 ***             
                  (0.01)                
MNov              -0.11 ***             
                  (0.01)                
sma1                           -0.66 ***
                               (0.08)   
----------------------------------------
AIC             -838.86      -726.62    
BIC             -785.75      -711.37    
Log Likelihood   436.43       368.31    
Num. obs.        168          156       
========================================

ACF,PACF检验：

par(mfrow=c(2,1), mar=c(3,5,3,3)) 
acf(model.ar3$residuals); pacf(model.ar3$residuals)
dev.off()

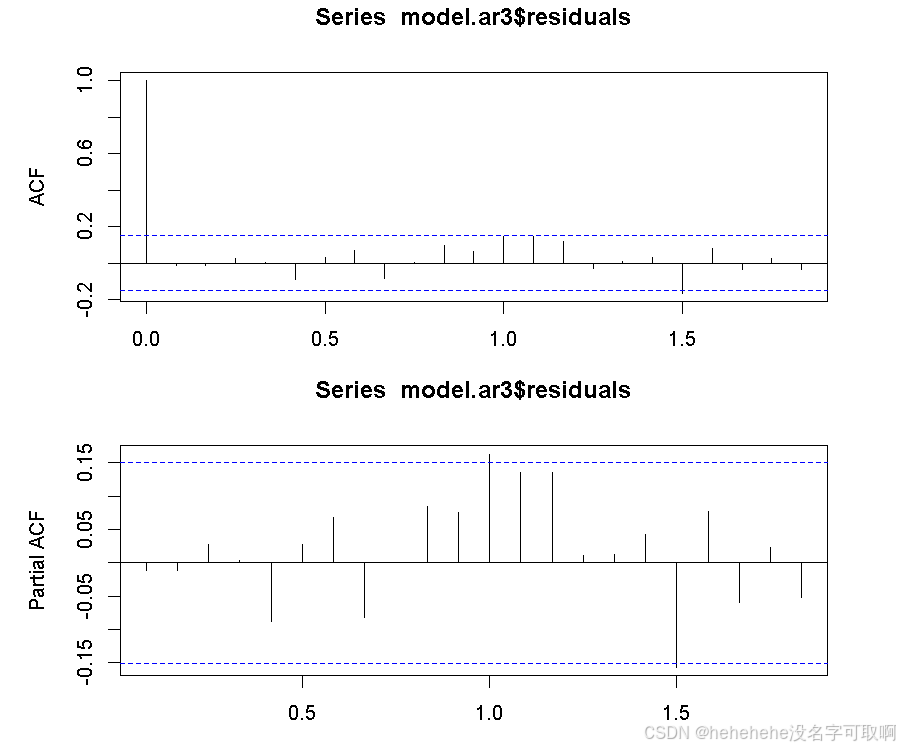
生成预测结果（略）：

t <- ((T+1):(T+h))
M <- I(seasonaldummy(y, h))
TrSeasL <- model.matrix(~ t + M)
AR3.Forecast <- forecast(model.ar3, h=h, xreg=TrSeasL)
AR3.Forecast

五、比较两个模型

1.比较预测结果

par(mfrow=c(2,1), mar=c(3,5,3,3)) 
plot(SAR3.Forecast, xlim=c(years-1, years+2)) # 季节性ARIMA模型的预测结果
plot(AR3.Forecast, xlim=c(years-1, years+2)) # 带有趋势和季节性成分的AR(3)模型的预测结果
dev.off()

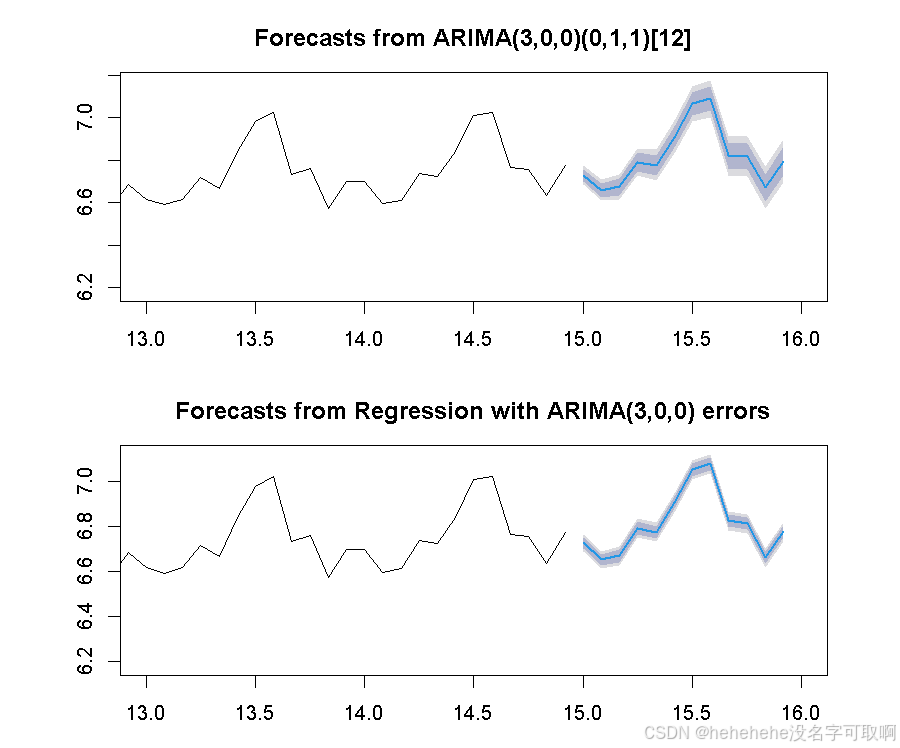
2. 比较预测精度

h <- s * 1
yy <- subset(y, end=length(y)-h)
zz <- subset(y, start=length(y)-h+1)
# y分割为测试集和训练集yy，zz

T <- length(yy) #set up the length of your data
t <- (1:T)
M <- seasonaldummy(yy)
TrSeasL <- model.matrix(~ t + M)
Tr.model.ar3 <- Arima(yy, order = c(3, 0, 0), include.mean = FALSE, xreg=TrSeasL)
t <- ((T+1):(T+h))
M <- seasonaldummy(zz)
TrSeasL <- model.matrix(~ t + M)
# 测试集和训练集yy，zz分别计算长度，创建时间变量，生成季节性虚拟变量矩阵等

AR3.Forecast <- forecast(Tr.model.ar3, h=h, xreg=TrSeasL)
# 构建训练集TSC模型，并对测试集进行预测

Tr.model.sar3 <- Arima(yy, order = c(3, 0, 0), seasonal = c(0, 1, 1))
SAR3.Forecast <- forecast(Tr.model.sar3, h=h)
# 构建训练集季节性ARIMA模型，并对测试集进行预测

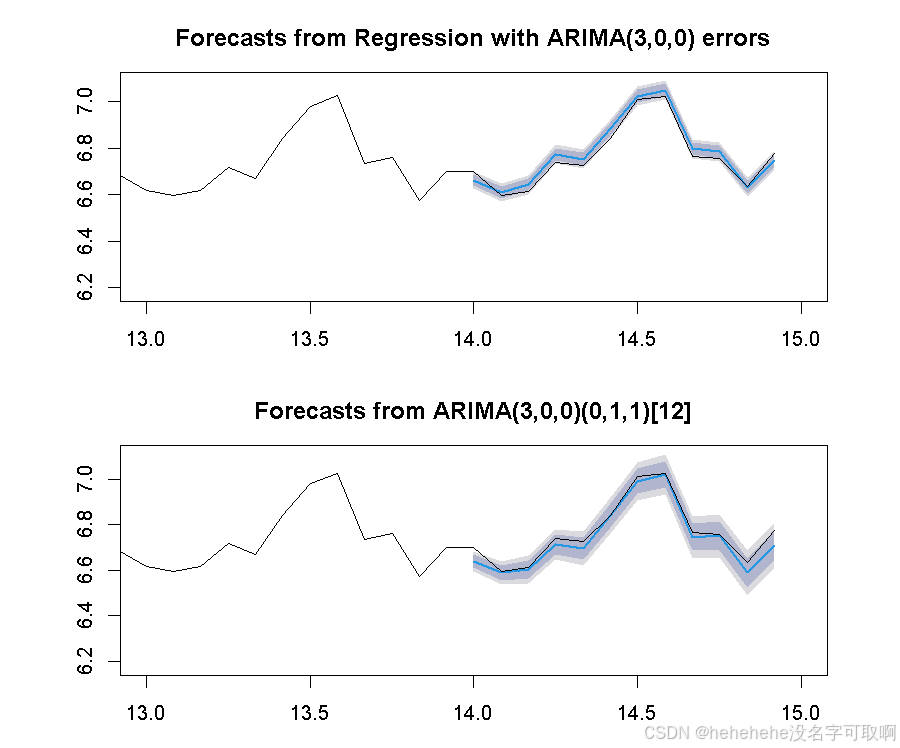
分别计算带有趋势和季节性成分的AR(3)模型和季节性ARIMA模型在测试集 zz 上的预测精度：

accuracy(AR3.Forecast, zz)
accuracy(SAR3.Forecast, zz)
par(mfrow=c(2,1), mar=c(3,5,3,3)) 
plot(AR3.Forecast, xlim=c(years-1, years+1)); lines(y)
plot(SAR3.Forecast, xlim=c(years-1, years+1)); lines(y)
dev.off()