- 数据来源主要为FRED(课程要求使用),代码部分来自于老师,参考用书:
1.Diebold FX Forecasting in Economics, Business, Finance and Beyond. University of Pennsylvania, 2017.
- available on-line http://www.ssc.upenn.edu/~fdiebold/Teaching221/Forecasting.pdf
2.Diebold FX Elements of Forecasting, 4th edition (Cengage Publishing, 2007).
- hard copy can be purchased used from on-line book stores
- available on-line http://www.ssc.upenn.edu/~fdiebold/Teaching221/BookPhotocopy.pdf
- author's version http://www.ssc.upenn .edu/~fdiebold/Teaching221/FullBook.pdf
预测步骤sum:
- 步骤 1:初步使用训练集和测试集来评估不同模型,找到表现最佳的模型(如 ARMA(2,1))。
- 步骤 2:使用整个数据集(包括训练和测试数据)重新拟合该模型,以便为未来预测提供最好的参数估计。
- 步骤 3:进行样本外预测,预测未来一段时间的数据(例如未来 12 个月或 12 个季度的数据)。
一、数据与前期准备
见:R语言时间序列学习+代码记录2:Modeling cycles - AR( ), MA( ), and ARMA( )
- 划分训练集和测试集
- 测试集:设置长度为两个完整的年度数据,即最后8个季度的数据(从
T-h+1到T)。 训练集: 从时间序列中取前T-h个数据点,即去掉最后两个年度的数据。
- 测试集:设置长度为两个完整的年度数据,即最后8个季度的数据(从
h <- s*2
y <- subset(data, end=T-h)
z <- subset(data, start=T-h+1)
二、MA(4) 模型预测
1.拟合模型
#拟合模型
model.ma <- arima(y,order=c(0,0,4))
model.ma
#拟合数据与残差(表示模型对数据的拟合程度,绘图用)
FIT.ma <- y - model.ma$residuals
y - model.ma$residuals: 获得模型拟合值(用模型解释数据后,在每个时间点的“预测值”)
拟合值=实际值−残差
Call:
arima(x = y, order = c(0, 0, 4))
Coefficients:
ma1 ma2 ma3 ma4 intercept
1.6619 1.7786 1.2891 0.5385 100.4851
s.e. 0.0752 0.1202 0.1197 0.0690 1.0553
sigma^2 estimated as 3.729: log likelihood = -267.79, aic = 547.57
2.预测未来数据
forecast(): 生成基于拟合模型的未来预测。forecast.ma: 保存了预测的结果,包括预测值及其置信区间。
forecast.ma <- forecast(model.ma, h=h)
forecast.ma
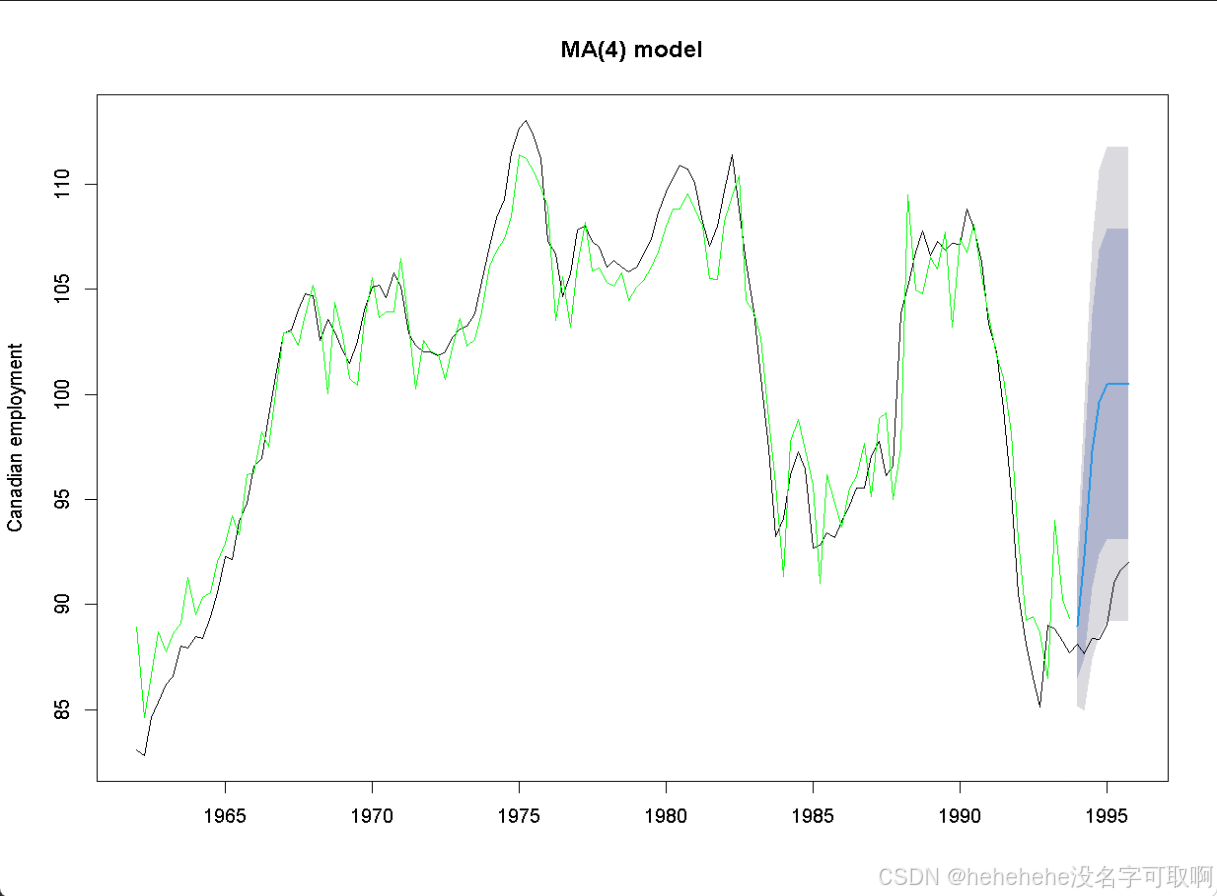
plot(forecast.ma, ylab="Canadian employment", main="MA(4) model")
# 在图中添加原始数据曲线,以对比实际值和预测值
lines(data)
# 在图中添加模型拟合数据的曲线,用绿色表示模型拟合的部分,便于与实际数据进行比较。
lines(FIT.ma, col="green")
> forecast.ma
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1994 Q1 88.96692 86.49220 91.44164 85.18216 92.75168
1994 Q2 92.27199 87.47210 97.07188 84.93119 99.61279
1994 Q3 97.33854 90.82604 103.85104 87.37853 107.29855
1994 Q4 99.61276 92.36089 106.86464 88.52198 110.70355
1995 Q1 100.48512 93.11181 107.85843 89.20861 111.76162
1995 Q2 100.48512 93.11181 107.85843 89.20861 111.76162
1995 Q3 100.48512 93.11181 107.85843 89.20861 111.76162
1995 Q4 100.48512 93.11181 107.85843 89.20861 111.76162
三、ARIMA(2,1)模型预测
1.拟合模型
model.arma<-arima(y,order=c(2,0,1))
model.arma
FIT.arma <- y - model.arma$residuals
Call:
arima(x = y, order = c(2, 0, 1))
Coefficients:
ar1 ar2 ma1 intercept
1.5674 -0.5912 -0.1479 97.7239
s.e. 0.1589 0.1584 0.1971 4.5113
sigma^2 estimated as 2.104: log likelihood = -231.2, aic = 472.39
2.预测未来数据
- 预测
forecast.arma <- forecast(model.arma, h=h)
forecast.arma
> forecast.arma
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1994 Q1 87.72955 85.87044 89.58865 84.88629 90.57281
1994 Q2 87.96930 84.74118 91.19741 83.03232 92.90628
1994 Q3 88.34300 83.91058 92.77541 81.56420 95.12179
1994 Q4 88.78699 83.31979 94.25420 80.42563 97.14836
1995 Q1 89.26200 82.91649 95.60750 79.55739 98.96661
1995 Q2 89.74404 82.65679 96.83129 78.90503 100.58305
1995 Q3 90.21877 82.50574 97.93180 78.42271 102.01484
1995 Q4 90.67790 82.43629 98.91952 78.07344 103.28236
- 绘图
plot(forecast.arma, ylab="Canadian employment", main="ARMA(2,1) model")
lines(data)
lines(FIT.arma, col="green")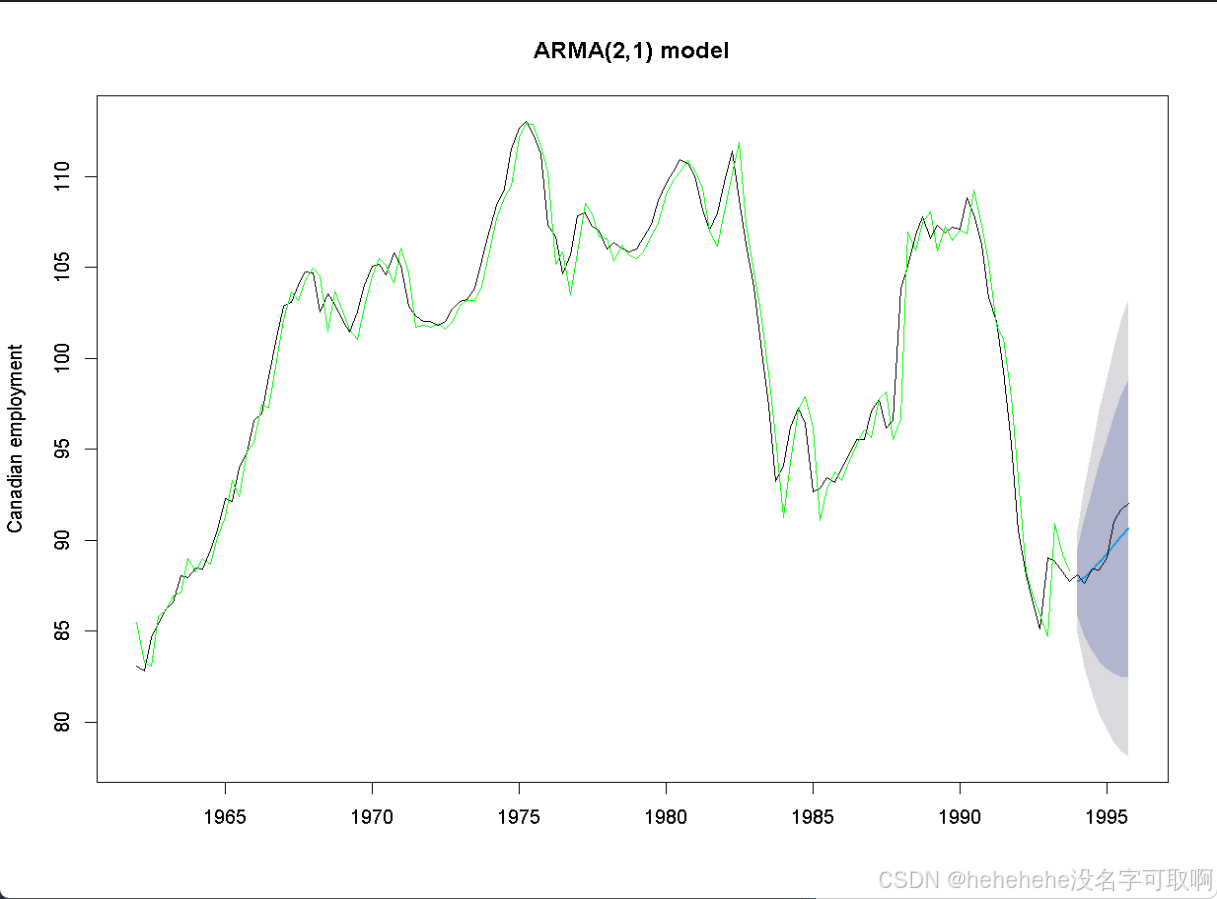
四、AR(2)模型预测
1.拟合模型
model.ar <- arima(y, order=c(2,0,0))
model.ar
FIT.ar <- y - model.ar$residuals
Call:
arima(x = y, order = c(2, 0, 0))
Coefficients:
ar1 ar2 intercept
1.4534 -0.4781 97.1679
s.e. 0.0773 0.0791 4.9505
sigma^2 estimated as 2.113: log likelihood = -231.48, aic = 470.95
2.预测未来数据
- 预测
forecast.ar <- forecast(model.ar, h=h)
forecast.ar
> forecast.ar
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1994 Q1 87.70072 85.83769 89.56376 84.85146 90.54999
1994 Q2 87.92248 84.63569 91.20928 82.89577 92.94920
1994 Q3 88.25689 83.77651 92.73726 81.40474 95.10903
1994 Q4 88.63688 83.17106 94.10271 80.27763 96.99614
1995 Q1 89.02930 82.74830 95.31030 79.42333 98.63526
1995 Q2 89.41795 82.45698 96.37893 78.77206 100.06385
1995 Q3 89.79521 82.26131 97.32911 78.27310 101.31732
1995 Q4 90.15770 82.13632 98.17908 77.89006 102.4253
- 绘图
plot(forecast.ar, ylab="Canadian employment", main="AR(2) model")
lines(data)
lines(FIT.ar, col="green")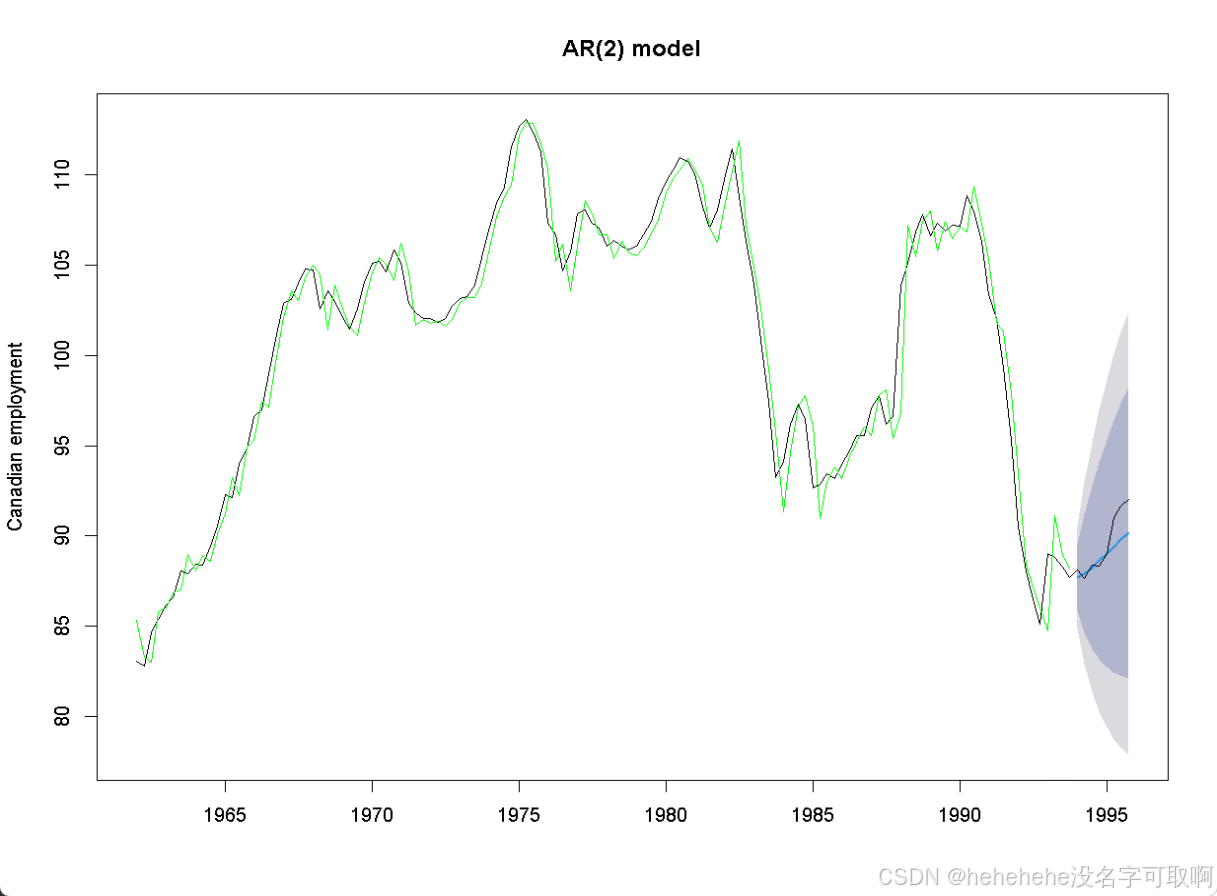
五、不同模型比较和验证
1.计算样本内预测的准确性
accuracy()函数:用于计算预测模型的准确性评估指标。输入预测值和实际值,输出结果包括多种误差度量指标,如:- ME(Mean Error):平均误差。
- RMSE(Root Mean Squared Error):均方根误差,衡量预测值与实际值之间的偏差。
- MAE(Mean Absolute Error):平均绝对误差,表示预测值与实际值的平均差异大小。
- MAPE(Mean Absolute Percentage Error):平均绝对百分比误差。
- ACF1:残差的自相关函数。
这里的forecast.ma、forecast.arma、forecast.ar分别是MA(4)、ARMA(2,1)和AR(2)模型的预测结果,而z是测试集的真实值。通过accuracy()函数,可以比较这些模型在样本内的预测表现。
accuracy(forecast.ma, z)
accuracy(forecast.arma, z)
accuracy(forecast.ar, z)
> accuracy(forecast.ma,z) ME RMSE MAE MPE MAPE MASE ACF1 Theil's U Training set 0.05096486 1.931035 1.577108 -0.05006405 1.599061 0.4419788 0.1279382 NA Test set -7.98390378 8.650933 7.983904 -8.89665683 8.896657 2.2374607 0.4729141 10.22794 > accuracy(forecast.arma,z) ME RMSE MAE MPE MAPE MASE ACF1 Theil's U Training set 0.08863764 1.4506686 1.0735893 0.07184749 1.0759698 0.3008696 -0.008750365 NA Test set 0.44098747 0.8665862 0.6836481 0.47889345 0.7537421 0.1915899 0.550008915 0.997462 > accuracy(forecast.ar,z) ME RMSE MAE MPE MAPE MASE ACF1 Theil's U Training set 0.09438165 1.453735 1.0835093 0.07803805 1.0862007 0.3036496 -0.03923956 NA Test set 0.66778902 1.110948 0.8035066 0.72894642 0.8831506 0.2251799 0.60409261 1.280792
结果表明:ARMA(2,1) 模型在所有误差度量(ME、RMSE、MAE等)中表现最好,说明该模型最适合此数据集。
1. MA 模型(forecast.ma):
-
测试集上的 RMSE 为 8.650933,MAE 为 7.983904,误差较大。
- Theil's U 指标为 10.22794,表明预测性能相当差,甚至可能比随机猜测更差。
2. ARMA(2,1) 模型(forecast.arma):
- 测试集上的 RMSE 为 0.8665862,MAE 为 0.6836481,误差较小。
- MAPE 为 0.7537421,低于其他模型,表明相对误差更小。
- Theil's U 为 0.997462,接近 1,但远小于 MA 模型,表明 ARMA(2,1) 模型的预测性能较好。
- 综合来看,ARMA(2,1) 在测试集上提供了最好的预测性能。
3. AR(2) 模型(forecast.ar):
- 测试集上的 RMSE 为 1.110948,MAE 为 0.8035066,虽然比 MA 模型好,但比 ARMA(2,1) 差。
- MAPE 为 0.8831506,也比 ARMA(2,1) 的 MAPE 更高。
- Theil's U 为 1.280792,大于 1,表示预测性能不如随机猜测。
2.使用完整数据集重新估计模型并进行样本外预测
在确定ARMA(2,1)为最佳模型后重新估计模型,并在整个数据集上进行样本外预测。
1. 为什么要重新估计模型?
- 在模型比较阶段,通常会使用 训练集 来调整和选择模型参数,并用 测试集 来评估模型的表现。
- 一旦确定最优模型,需要使用 完整的数据集(包含训练集和测试集的全部数据)来重新估计模型。这是因为训练和测试集分开使用时,模型没有利用全部数据。为了在未来预测中最大限度地利用现有信息,模型需要基于所有可用的数据重新进行拟合。
- 通过使用完整的数据集,模型的参数估计会更准确,这样它对数据的学习更加全面,可以提高预测未来数据的能力。
2. 什么是样本外预测?
样本外预测(Out-of-Sample Prediction),是指使用模型对 未来未见过的数据 进行预测。用已有的历史数据训练模型,然后让模型去预测 未来的数据,即不在训练数据范围内的新数据。
样本外预测的步骤通常如下:
- 使用历史数据训练模型:例如,有2000年至2020年的数据,用它们来拟合模型。
- 预测未来数据:模型在被训练之后,可以用来预测2021年及以后的数据。由于2021年及以后的数据并未包含在训练集或测试集中,预测这些数据就称为 样本外预测。
3. 样本外预测的必要性
样本外预测的关键意义在于,它可以评估模型的 泛化能力,即模型在面对未来的未知数据时是否能给出准确的预测。训练集和测试集都属于 样本内数据,即已经观测到的数据,而样本外预测针对的是完全新的数据,这也是我们在现实中最关心的问题:模型在未来的实际应用中是否能准确预测。
- 模型的实际应用价值:在真实世界中通常并不只是关心模型在历史数据上的表现,更关心它能否在未来的实际场景中有效应用。因此,样本外预测提供了对未来数据进行预测的模拟。
- 模型的鲁棒性:即使在历史数据上表现良好,也不保证它在未来数据上同样能有好的表现。样本外预测能够检测模型在遇到新数据时是否具有稳健的预测能力。
- 避免过拟合:在模型拟合过程中,过拟合是常见的问题。过拟合意味着模型在历史数据上表现很好,但对新数据(样本外数据)无法做出准确预测。通过样本外预测,可以测试模型是否过度依赖训练数据中的噪声,进而验证模型的泛化能力。
# 将完整的数据集(即之前训练集和测试集的合并)用于模型拟合
y <- data
h <- 12
model.arma <- arima(y, order=c(2,0,1))
model.arma
acf(model.arma$residuals)
pacf(model.arma$residuals)
FIT.arma <- y - model.arma$residuals
forecast.arma <- forecast(model.arma, h=h)
forecast.arma
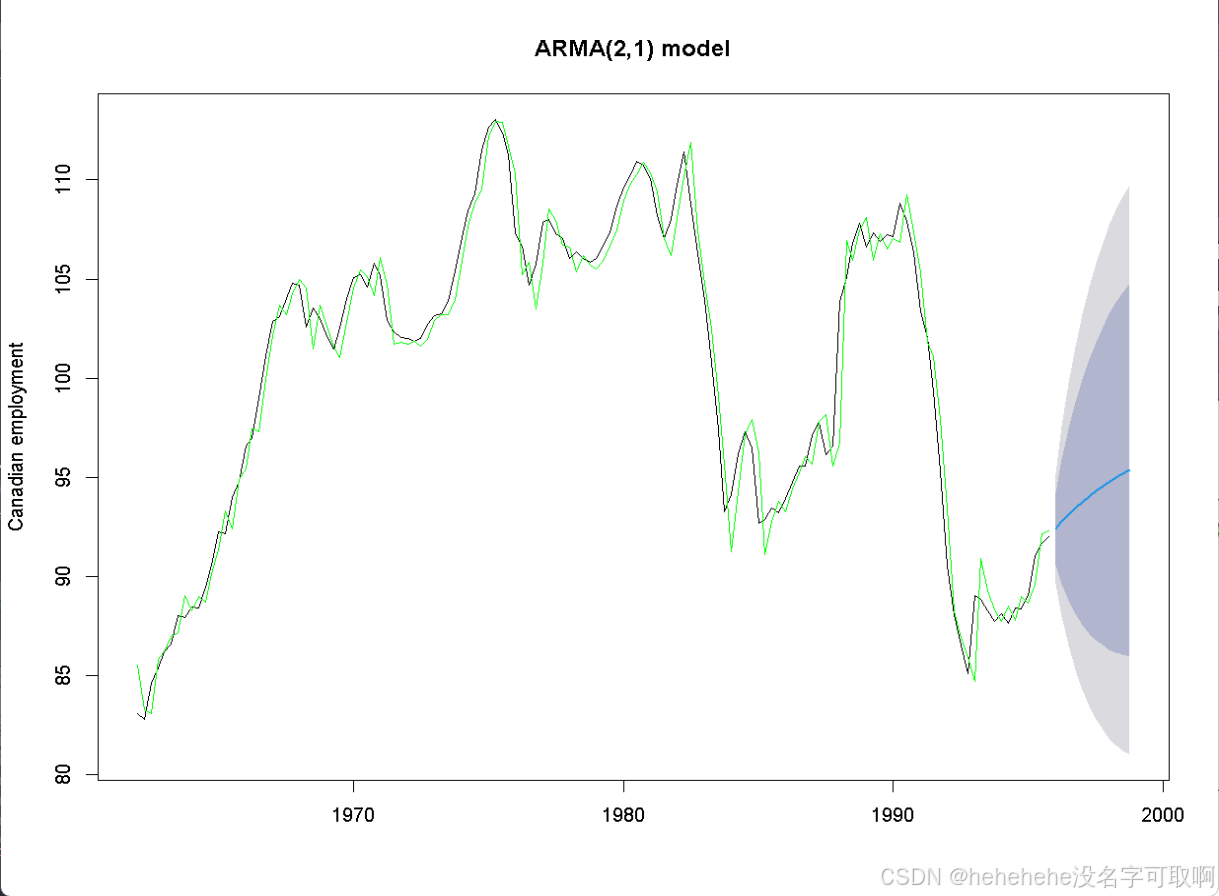
plot(forecast.arma, ylab="Canadian employment", main="ARMA(2,1) model")
lines(FIT.arma, col="green")
#here is the out-of-sample forecast
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1996 Q1 92.40745 90.58986 94.22504 89.62769 95.18721
1996 Q2 92.77623 89.62953 95.92292 87.96377 97.58868
1996 Q3 93.12185 88.80440 97.43931 86.51887 99.72483
1996 Q4 93.44525 88.12048 98.77002 85.30172 101.58878
1997 Q1 93.74751 87.56735 99.92767 84.29577 103.19924
1997 Q2 94.02979 87.12760 100.93198 83.47380 104.58578
1997 Q3 94.29328 86.78281 101.80375 82.80701 105.77955
1997 Q4 94.53914 86.51606 102.56221 82.26890 106.80937
1998 Q1 94.76849 86.31273 103.22425 81.83652 107.70045
1998 Q2 94.98240 86.16059 103.80420 81.49061 108.47418
1998 Q3 95.18189 86.04964 104.31413 81.21532 109.14846
1998 Q4 95.36791 85.97169 104.76413 80.99763 109.73819





















 1447
1447

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








