R语言时间序列学习+代码记录4： Random Walk, ARIMA Forecasting Models

本文链接：https://blog.youkuaiyun.com/lxyhehehehe/article/details/143335428

数据来源主要为FRED（课程要求使用），代码部分来自于老师，参考用书：
1.Diebold FX Forecasting in Economics, Business, Finance and Beyond. University of Pennsylvania, 2017.
- available on-line http://www.ssc.upenn.edu/~fdiebold/Teaching221/Forecasting.pdf
2.Diebold FX Elements of Forecasting, 4th edition (Cengage Publishing, 2007).
- hard copy can be purchased used from on-line book stores
- available on-line http://www.ssc.upenn.edu/~fdiebold/Teaching221/BookPhotocopy.pdf
- author's version http://www.ssc.upenn .edu/~fdiebold/Teaching221/FullBook.pdf

一、背景和原理

时间序列分析中平稳性是一个重要的假设。许多模型（ARMA、ARIMA等）在分析和预测时间序列时都要求数据是平稳的。如果一个序列具有单位根（即非平稳），它就会呈现出趋势或其他随时间变化的特性，导致模型参数的不稳定和预测结果的不准确。因此，DF检验的主要目的是通过检验单位根的存在，来确认时间序列是否平稳。

1.单位根：

定义为AR(1)模型的一种特性：

$y_t = \rho y_{t-1} + \epsilon_t$

其中， $y_t$ 是当前时间的观测值， $y_{t-1}$ 是前一时刻的观测值， $\epsilon_t$ 是白噪声项。这里的关键是参数 $\rho$ ：

如果 $|\rho| < 1$ ，则 $y_t$ 是平稳的（自回归的过程）
如果 $\rho = 1$ ，则 $y_t$ 是非平稳的（随机游走过程）
如果 $|\rho| > 1$ ，则序列会发散

单位根意味着 $\rho = 1$ ，即序列不具备均值回归的特性，不能返回一个稳定的长期均值。

2.漂移项（drift term）

指一种常数项，通常表示时间序列中固定的非零平均增长或下降趋势。当一个时间序列模型包含漂移项时，即使时间序列本身是随机的或没有明确的趋势，它仍然会围绕一个非零的平均值“漂移”或逐渐增加/减少。漂移项通常出现在带常数的时间序列模型中。以简单的AR(1)模型（自回归模型）为例：

$y_t = \alpha + \rho y_{t-1} + \epsilon_t$

其中 $\alpha$ 是漂移项，它在模型中会推动时间序列向一个非零的长期趋势发展。若它不等于零，序列的长期均值将不为零，即序列会有某种长期的增长或减少的趋势。

反映长期的平均变化：在随机波动之上，序列整体可能有向某个方向的趋势
区分白噪声和随机游走：随机游走模型若带有漂移项，则为“带漂移的随机游走”，意味着其在没有冲击时会沿漂移项方向持续变化
经济和金融意义：在经济和金融时间序列中，漂移项往往表示一种基本的增长或减少趋势。例如，GDP、股价等数据的增长通常不仅仅由随机因素决定，还受到某种基础增长（即漂移）的影响

在实际分析中，决定是否包含漂移项往往是根据数据特性和经济意义而定的：

若时间序列围绕一个非零的长期均值上下波动，则包含漂移项可能更合适
若数据显然围绕零均值波动，则可以省略漂移项

在模型拟合和检验中（如ADF检验），正确选择漂移项也会影响统计结果的准确性。忽略漂移项可能导致误判，即将存在趋势的序列误判为单位根序列。

2.Dickey-Fuller检验

Dickey-Fuller（DF）检验：用于检验时间序列数据中是否存在单位根的统计方法。单位根是指一个时间序列具有随机游走特性，这种情况下，序列并不是平稳的。DF检验帮助我们判断一个序列是否是平稳序列（即平均值、方差和自协方差不随时间变化），或者是否需要进行差分处理来使其平稳。

通过对AR(1)模型的参数 $\rho$ 进行假设检验，以确定序列是否存在单位根。DF检验的检验假设为：

原假设（H0）： $\rho = 1$ ，即序列存在单位根，是非平稳的
备择假设（H1）： $\rho < 1$ ，即序列是平稳的

为了进行检验，将模型重写为：

$\Delta y_t = \alpha + \beta t + \gamma y_{t-1} + \epsilon_t$

其中， $\Delta y_t = y_t - y_{t-1}$ ，是时间序列的差分； $\alpha$ 是常数项； $\beta t$ 表示时间趋势； $\gamma$ 是 $y_{t-1}$ 的系数，用来测试单位根的存在性； $\epsilon_t$ 是白噪声项。
根据单位根的定义，可以推出 $\gamma = \rho - 1$ ，因此：

若 $\rho = 1$ ，则 $\gamma = 0$ （表示存在单位根，序列非平稳）
若 $\rho < 1$ ，则 $\gamma < 0$ （表示序列平稳）

Dickey-Fuller检验的本质在于对 $\gamma$ 进行统计检验，判断它是否显著小于0。

根据不同的模型设定，DF检验可以分为以下几种类型：

无常数无趋势的DF检验： $\Delta y_t = \gamma y_{t-1} + \epsilon_t$
带常数无趋势的DF检验： $\Delta y_t = \alpha + \gamma y_{t-1} + \epsilon_t$
带常数带趋势的DF检验： $\Delta y_t = \alpha + \beta t + \gamma y_{t-1} + \epsilon_t$

选择哪种形式的DF检验需要根据时间序列的特性来判断。如果序列看起来没有显著的趋势项，可以选用前两种模型；如果存在时间趋势，通常使用带常数和趋势的形式。

3.Augmented Dickey-Fuller（ADF）检验

Dickey-Fuller检验有一个扩展版本，即Augmented Dickey-Fuller（ADF）检验，用于处理存在序列自相关的问题。ADF检验在DF检验的基础上加入了滞后项来消除序列自相关的影响。ADF检验的模型为：

$\Delta y_t = \alpha + \beta t + \gamma y_{t-1} + \sum_{i=1}^{p} \delta_i \Delta y_{t-i} + \epsilon_t$

其中 $\sum_{i=1}^{p} \delta_i \Delta y_{t-i}$ 是滞后项的加总，用于消除序列自相关。

进行DF或ADF检验后，根据p值和临界值判断是否拒绝原假设：

p值 < 显著性水平：拒绝原假设，序列平稳
p值 ≥ 显著性水平：无法拒绝原假设，序列可能存在单位根，是非平稳的

如果非平稳，则通常需要进行差分处理，变成平稳序列后再进行进一步的建模和预测

二、前期准备

1.数据示例

301.7865765
277.4617796
261.8486515
265.4914246
264.6482824
264.4942869
264.5432661
265.2238489
265.4773282
266.3328628
278.233772
（1:283）

2.基础参数设置

#Useful application-specific numbers block
s <- 12 #数据频率
datastart <- c(styear,1) #数据起始时间-January1 1973

3.转换为时间序列并绘图

data <- ts(data,start=datastart,frequency=s)
data <- log(data)
plot(data)

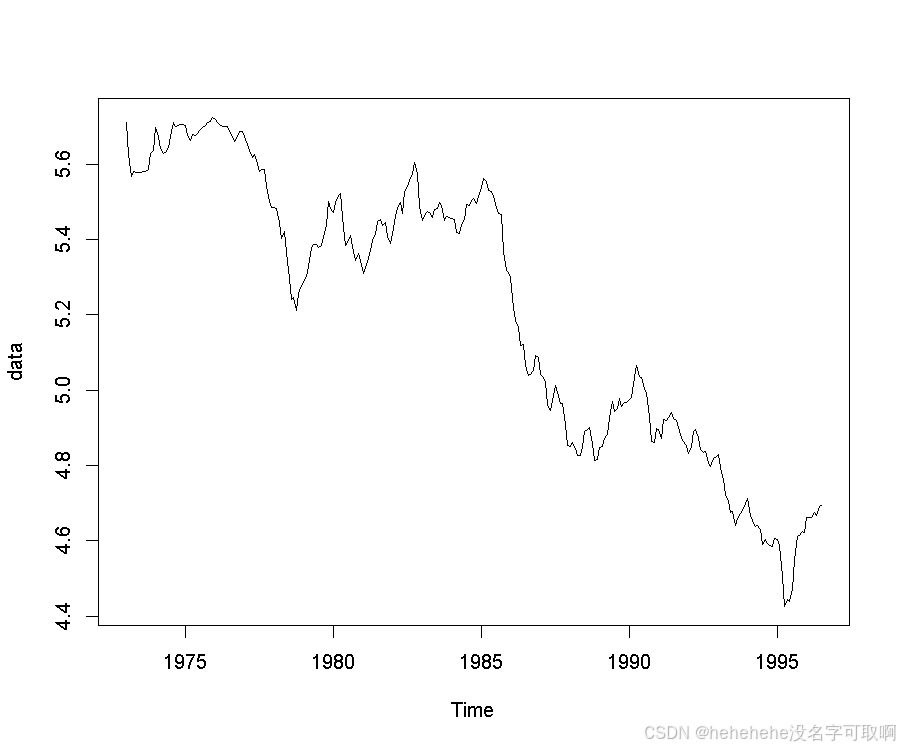
图像类似于单位根图像，考虑进行一阶差分

三、差分与检验

1.差分操作（以去除趋势）

diff() 函数：对时间序列进行一阶差分，计算相邻数据点之间的差值。一阶差分通常用于消除数据中的趋势，使得数据更加平稳。绘制差分后的时间序列图，以观察是否消除了趋势：

plot(diff(data))

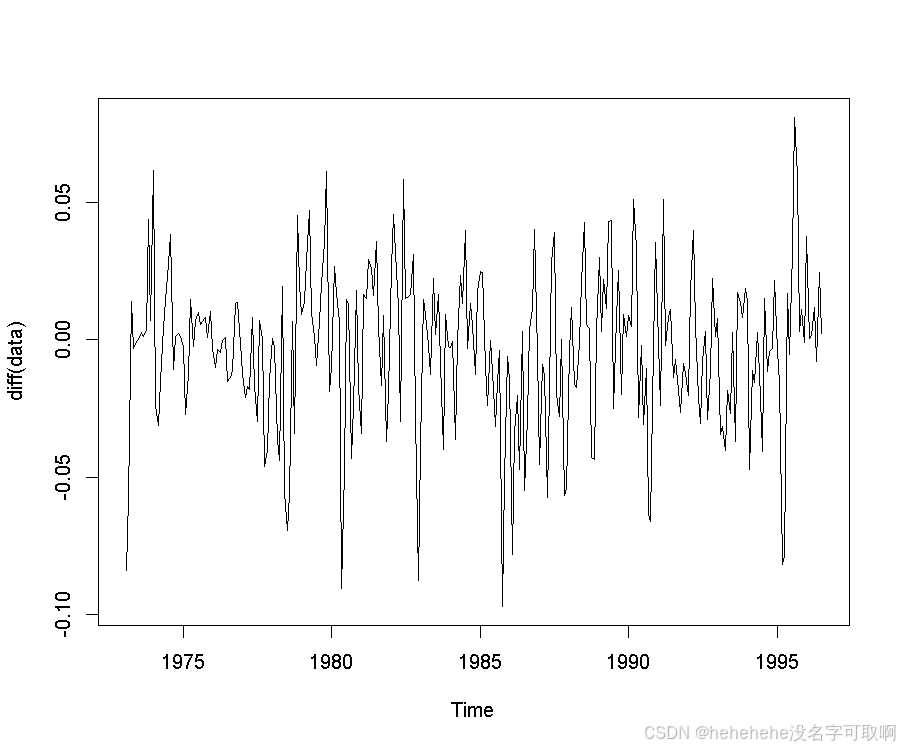
数据看起来接近平稳状态（白噪声），因此可能不再具有单位根。

2.自相关性分析

（1）自相关函数 (ACF) 和偏自相关函数 (PACF) ：

ACF检查一个序列在不同滞后下的自相关性。PACF检查在排除了之前滞后的影响后，时间序列在某个特定滞后点的自相关性。

par(mfrow=c(2,1), mar=c(3,5,3,3)) 
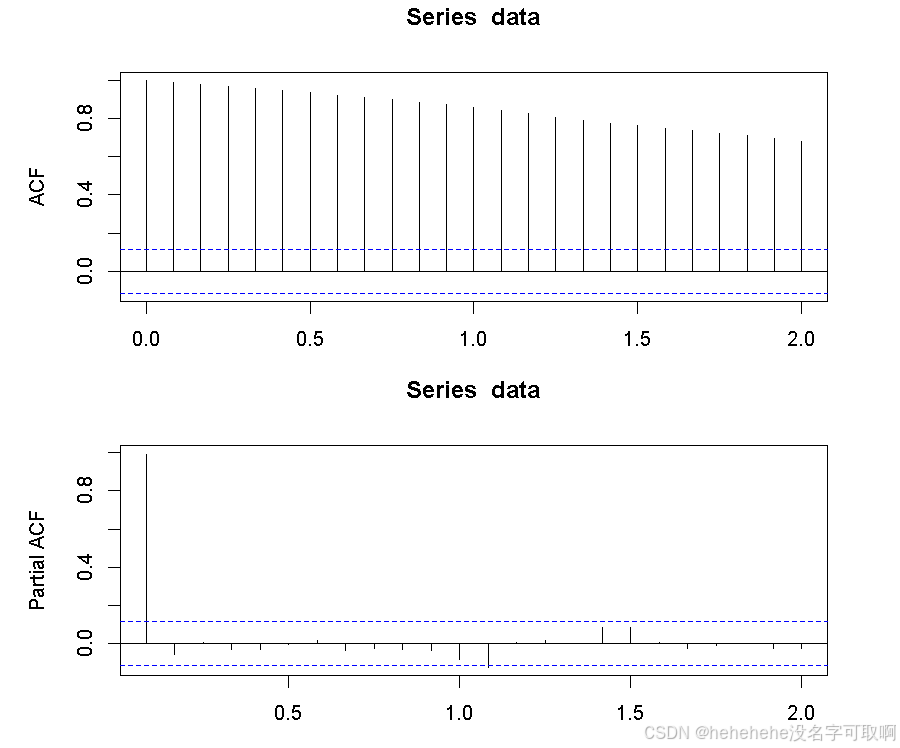
acf(data)
pacf(data)

结果显示，自相关函数的值接近 1，并且衰减得很慢，表明数据可能存在单位根。第一个偏自相关系数接近 1，而其他的系数都不显著。

（3）差分后的 ACF 和 PACF

acf(diff(data))
pacf(diff(data))

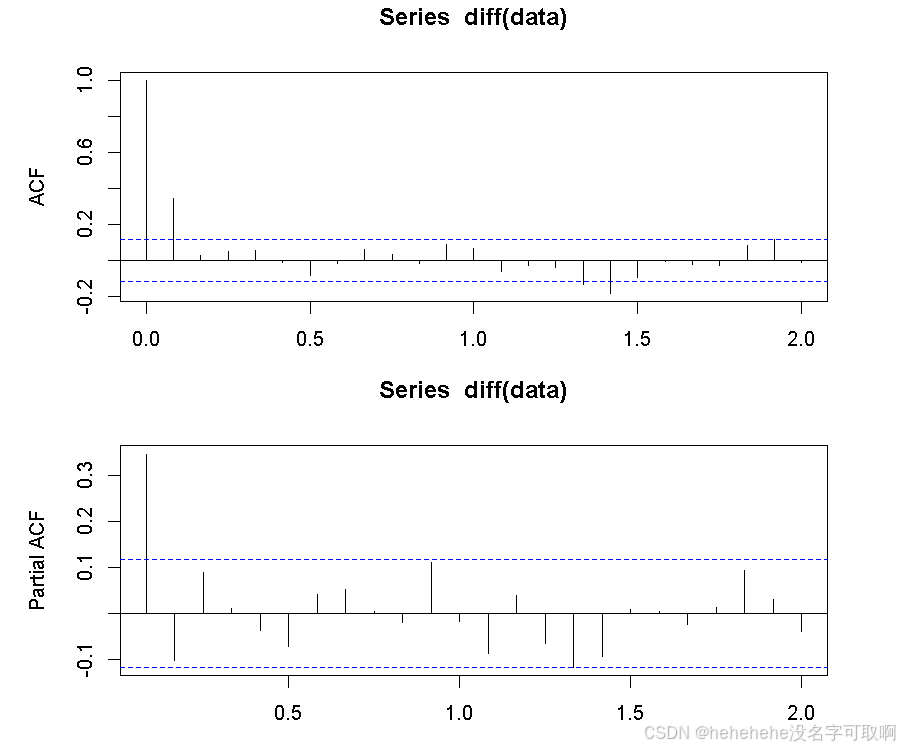
差分后的 ACF 和 PACF 图表明自相关函数迅速衰减，偏自相关函数也很快趋近零，表明差分后的序列是平稳的。在滞后1阶（lag 1）存在显著但较小的自相关，表明 ln(yen) 序列是I(1)过程。也就是说，ln(yen) 经过一次差分后变为平稳序列。

3.单位根检验（Dickey-Fuller 测试）

（1）对原始数据

test <- ur.df(data,type=c("trend"),lags=10,selectlags="AIC")
summary(test)
# type=c("trend")：在模型中包含一个趋势项（即考虑到时间序列中的线性趋势）
# ags=10：表示使用10个滞后项来提高模型的拟合效果
# selectlags="AIC"：使用Akaike信息准则 (AIC) 来自动选择最优的滞后阶数

Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.089822 -0.013508  0.002125  0.016710  0.074618 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.823e-01  7.121e-02   2.559   0.0110 *  
z.lag.1     -3.152e-02  1.217e-02  -2.589   0.0101 *  
tt          -1.403e-04  5.686e-05  -2.467   0.0143 *  
z.diff.lag1  3.898e-01  6.010e-02   6.485 4.29e-10 ***
z.diff.lag2 -1.105e-01  6.426e-02  -1.720   0.0866 .  
z.diff.lag3  1.033e-01  6.064e-02   1.703   0.0897 .  
---

Residual standard error: 0.02619 on 266 degrees of freedom
Multiple R-squared:  0.154,	Adjusted R-squared:  0.1381 
F-statistic: 9.682 on 5 and 266 DF,  p-value: 1.653e-08

Value of test-statistic is: -2.5894 2.9333 3.3614 

Critical values for test statistics: 
      1pct  5pct 10pct
tau3 -3.98 -3.42 -3.13
phi2  6.15  4.71  4.05
phi3  8.34  6.30  5.36

结果表明不能拒绝单位根假设，即原始数据中有单位根，数据是非平稳的。

（2）对差分数据

test <- ur.df(diff(data), type=c("drift"), lags=10, selectlags="AIC")
summary(test)
# type=c("drift") -模型中只包含一个漂移项，不再考虑趋势

Call:
lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.094391 -0.014119  0.002234  0.017817  0.073140 
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.002491   0.001628  -1.530    0.127    
z.lag.1     -0.716868   0.069517 -10.312   <2e-16 ***
z.diff.lag   0.093134   0.060611   1.537    0.126    
---
Residual standard error: 0.02651 on 268 degrees of freedom
Multiple R-squared:  0.3339,	Adjusted R-squared:  0.3289 
F-statistic: 67.18 on 2 and 268 DF,  p-value: < 2.2e-16

Value of test-statistic is: -10.3122 53.1706 

Critical values for test statistics: 
      1pct  5pct 10pct
tau2 -3.44 -2.87 -2.57
phi1  6.47  4.61  3.79

结果表明可以拒绝单位根假设，即差分后的数据是平稳的。

四、ARMA模型拟合

1.样本内预测

model.arima <- auto.arima(data, d=1, seasonal = FALSE, ic = "aic", 
                          stepwise = FALSE, approximation = FALSE, 
                          trace = TRUE)
model.arima
h <- s
forecast.arima<-forecast(model.arima, h=h)
forecast.arima #here is the insample forecast
plot(forecast.arima,ylab="Log JPY/USD Exchange Rate",main="MA(1) in first differences of Log JPY/USD Exchange Rate")

根据结果，ARIMA(0,1,1) with drift，即 MA(1)为最佳模型，表明一阶差分后的数据适合用移动平均模型来描述。预测表现：

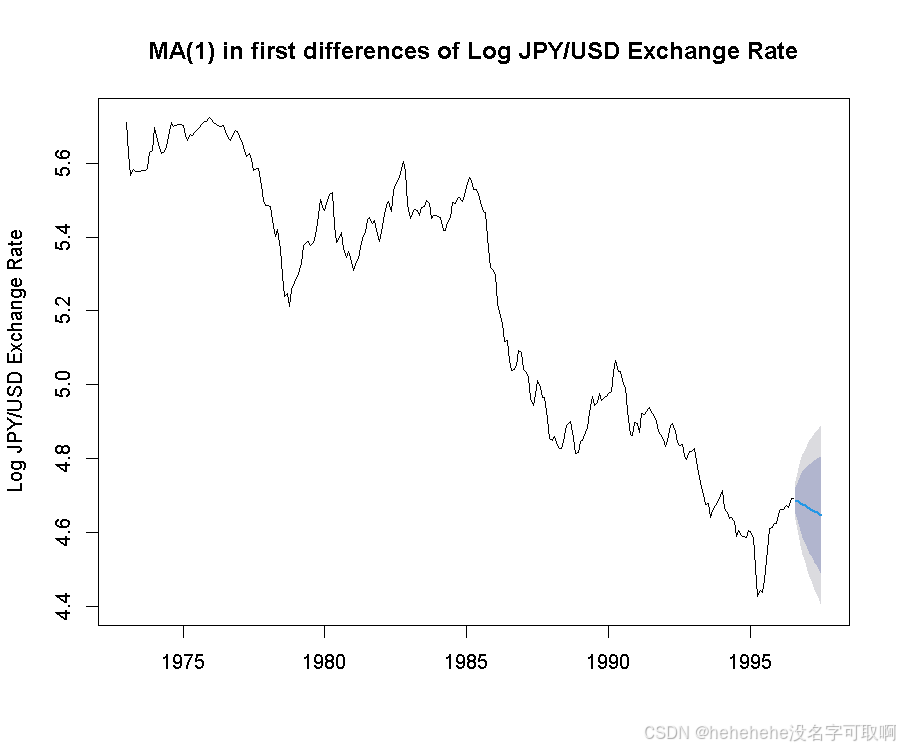
2.样本外预测

# 划分训练集测试集
h <- 19 #1.5 years of monthly data
y <- subset(data, end=length(data)-h); z <- subset(data, start=length(data)-h+1)
# 一阶差分模型
model.arima <- auto.arima(y, d=1, seasonal = FALSE, ic = "aic", 
                         stepwise = FALSE, approximation = FALSE, 
                         trace = TRUE)
model.arima

结果表明一阶差分后的数据表现为一阶移动平均模型，且数据在差分后仍有一定的漂移项（ARIMA(0,1,1) with drift）。如果预测的时间跨度（ℎ）比MA模型的阶数（q）大，则MA部分在长时间预测中的影响较小，此时更应该关注AR（自回归）部分的影响。将重点放在AR成分上，最佳模型为带有漂移项的ARIMA(3,1,0)模型。

# 指定ARIMA(3,1,0)模型并计算残差
arima310 <- Arima(y, order = c(3,1,0), include.drift = TRUE)
arima310
e <- arima310$residuals
# 残差的 ACF 和 PACF 分析
par(mfrow=c(2,1), mar=c(3,5,3,3))
acf(e)
pacf(e)
dev.off()

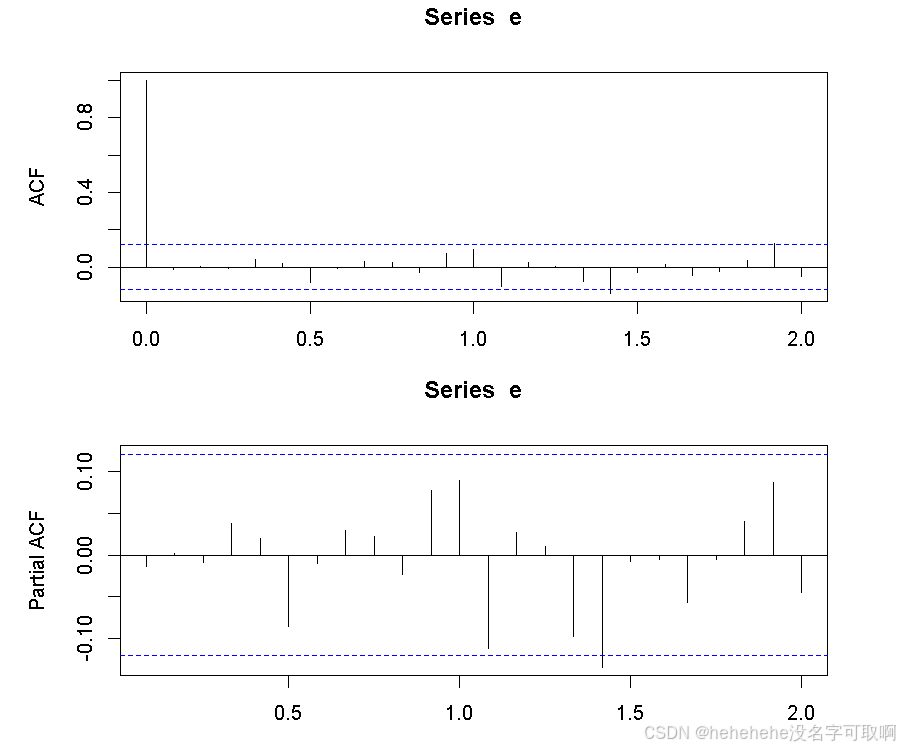
生成拟合值，可视化预测结果：

FIT.arima <- y - e
forecast.arima <- forecast(arima310, h=h)
forecast.arima
plot(forecast.arima, ylab="Log JPY/USD Exchange Rate", 
     main="AR(3) in first differences of Log JPY/USD Exchange Rate")
lines(data)
lines(FIT.arima, col="green")

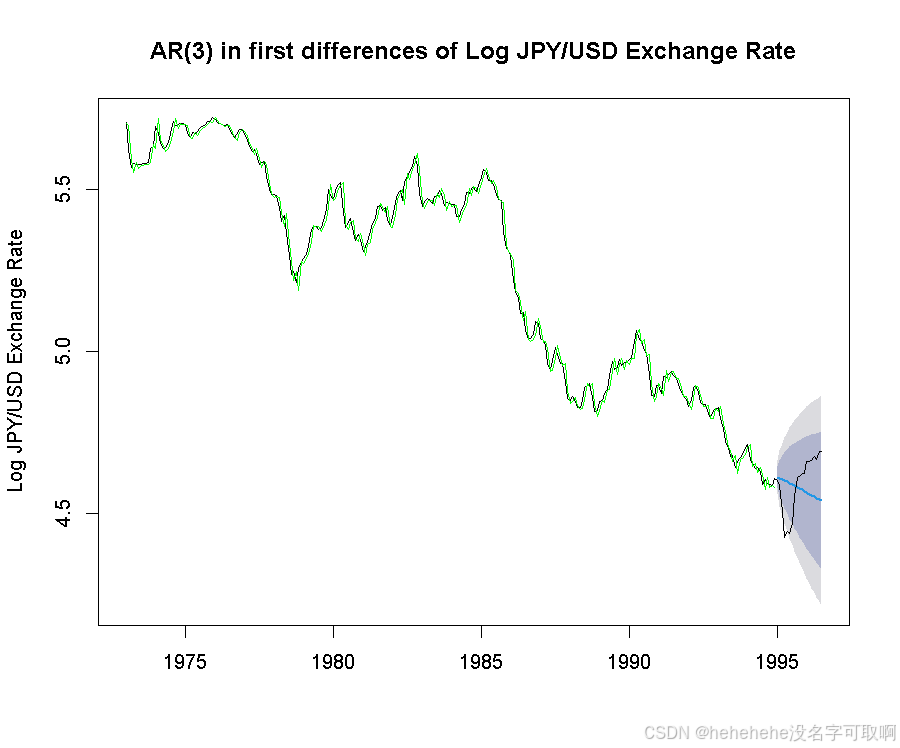
五、拟合带有确定性趋势的 ARMA 模型

T <- length(y)
model.arma <- auto.arima(y, d=0, xreg=1:T, seasonal = FALSE, ic = "aic", 
                          stepwise = FALSE, approximation = FALSE, 
                          trace = TRUE)
# d=0，不进行差分
# xreg=1:T，模型中加入了一个外生回归变量 1:T，这里用时间序列 1, 2, ... , T 作为确定性趋势。
model.arma

结果显示：Best model: Regression with ARIMA(1,0,1)。

1.模型选择tips：

AIC 信息准则表明 ARMA(3,1) 是最优的，但 SIC信息准则认为 AR(2) 更优。通常较高阶的模型可能会带来更好的拟合效果，但会损失更多的自由度（即有效数据点）。对于长期预测，MA 部分的影响可能变小，因此选择更低阶的 AR 成分可能更合理。

2.模型构建与预测

# 创建ARMA(1,1)带趋势项模型，并计算残差
arima101 <- Arima(y, order = c(1,0,1), xreg=1:T)
arima101
e <- arima101$residuals

# 自相关性检验
par(mfrow=c(2,1), mar=c(3,5,3,3)) 
acf(e)
pacf(e)
dev.off()

生成拟合值，可视化预测结果：

FIT.arma <- y - e
forecast.arma <- forecast(arima101, h=h, xreg=((T+1):(T+h)))
forecast.arma
# xreg=((T+1):(T+h)) -为预测期引入趋势项，以保持预测的线性趋势

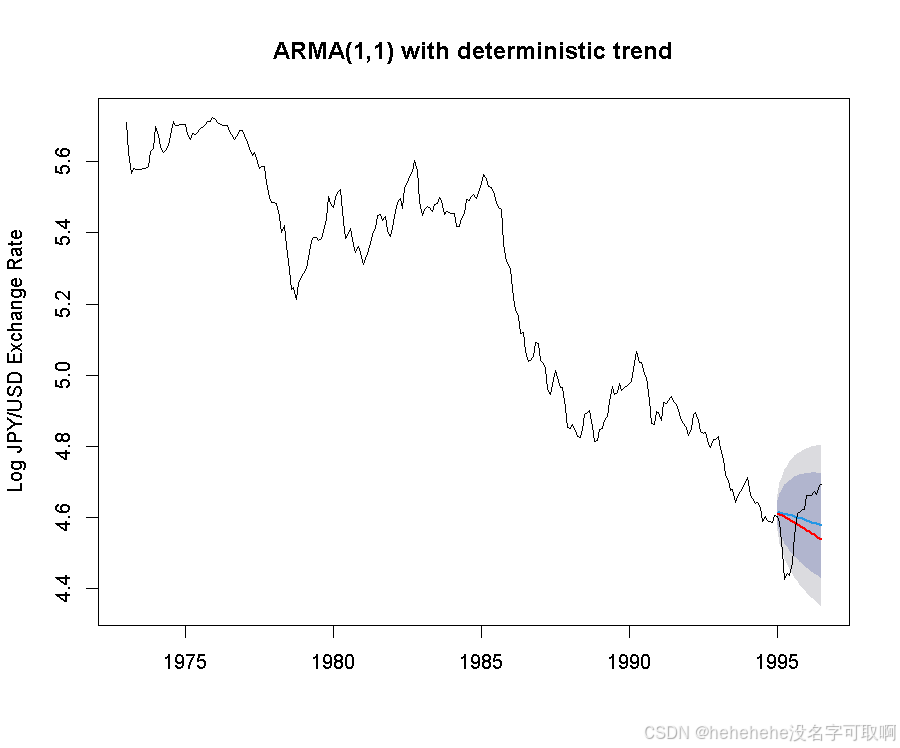
3. 计算预测精度并比较两个模型

accuracy(forecast.arima, z)
accuracy(forecast.arma, z)
# 计算两个模型在测试集 z 上的预测精度。这些指标包括：
# ME（Mean Error）：平均误差，衡量预测值与实际值的偏差。
# RMSE（Root Mean Squared Error）：均方根误差，衡量预测值与实际值之间误差的平均水平，越小越好。
# MAE（Mean Absolute Error）：平均绝对误差，表示预测误差的平均绝对值。

> accuracy(forecast.arima,z)
                       ME       RMSE        MAE          MPE      MAPE      MASE
Training set 0.0001249641 0.02574139 0.01959613 0.0008208646 0.3759094 0.1835944
Test set     0.0132900018 0.10725074 0.09419973 0.2451318490 2.0587235 0.8825490
                    ACF1 Theil's U
Training set -0.01398835        NA
Test set      0.88681601  2.830678
> accuracy(forecast.arma,z)
                        ME       RMSE        MAE          MPE      MAPE      MASE
Training set  0.0003143606 0.02561181 0.01940991  0.002647277 0.3721262 0.1818498
Test set     -0.0080564482 0.09746217 0.08127443 -0.216493809 1.7846402 0.7614529
                    ACF1 Theil's U
Training set 0.008244072        NA
Test set     0.880531347  2.593149

预测精度结果表明ARMA(1,1) 带确定性趋势模型的效果更好，在各项指标上都优于 ARIMA 模型。