本文详细介绍了回文子序列的概念及其实现方法，包括最长回文子序列与最长回文子串的递归与动态规划解决方案，并对比了不同算法的时间复杂度。
欢迎访问https://blog.youkuaiyun.com/lxt_Lucia～～
宇宙第一小仙女\(^o^)/～～萌量爆表求带飞=≡Σ((( つ^o^)つ~dalao们点个关注呗～～
一、概念
1、回文（palindrome）
回文就是正读和反读都一样的字符串，如aba，abba，abcba等。
2、字符子串和字符子序列的区别
（1）字符字串指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。
（2）字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符，即可以去掉字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。再如cabbeaf，删掉‘c’、'e'、' f '后剩下的子串“abba”就是回文字符串，也是其中最长的回文子序列。
（3）最长回文子串必须是连续的，而最长回文子序列不一定连续，但不可改变先后顺序。
二、最长回文子序列 and 最长回文子串
（一）最长回文子序列 LPS（Longest Palindromic Subsequence）
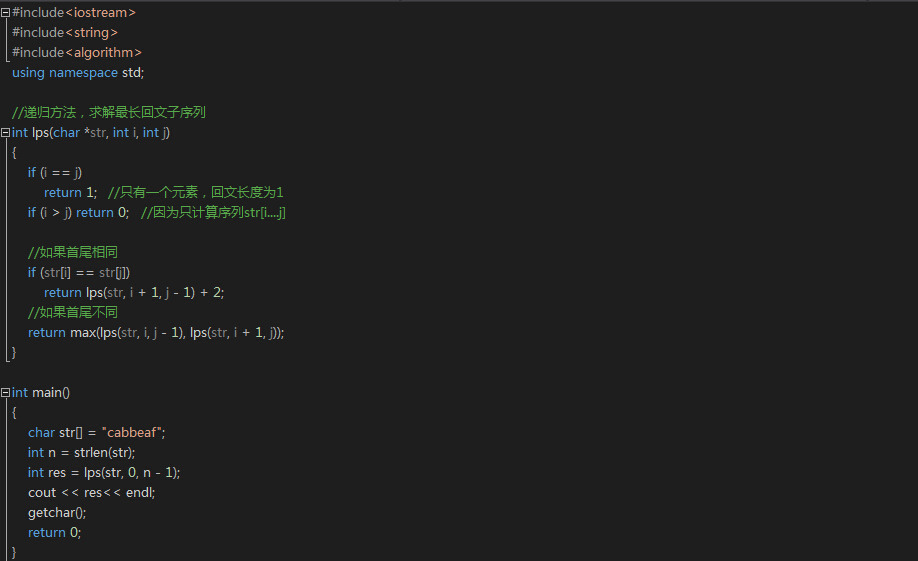
方法一：递归方法
str[0...n-1]是给定的字符串序列，长度为n，假设lps(0,n-1)表示序列str[0...n-1]的最长回文子序列的长度。
1.如果str的最后一个元素和第一个元素是相同的，则有：lps(0,n-1)=lps(1,n-2)+2；例如字符串序列“AABACACBA”，第一个元素和最后一个元素相同，其中lps(1,n-2)表示红色部分的最长回文子序列的长度；
2.如果str的最后一个元素和第一个元素是不相同的，则有：lps(0,n-1)=max(lps(1,n-1),lps(0,n-2))；例如字符串序列“ABACACB”，其中lps(1,n-1)表示去掉第一元素的子序列，lps(0,n-2)表示去掉最后一个元素的子序列。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
//递归方法，求解最长回文子序列
int lps(char *str, int i, int j)
{
if (i == j)
return 1; //只有一个元素，回文长度为1
if (i > j) return 0; //因为只计算序列str[i....j]
//如果首尾相同
if (str[i] == str[j])
return lps(str, i + 1, j - 1) + 2;
//如果首尾不同
return max(lps(str, i, j - 1), lps(str, i + 1, j));
}
int main()
{
char str[] = "cabbeaf";
int n = strlen(str);
int res = lps(str, 0, n - 1);
cout << res<< endl;
getchar();
return 0;
}
重叠子问题
但是通过上面递归的方法，会出现很多重复的计算，比如上面的L(1,4)，所以可以采用动态规划的方法求解
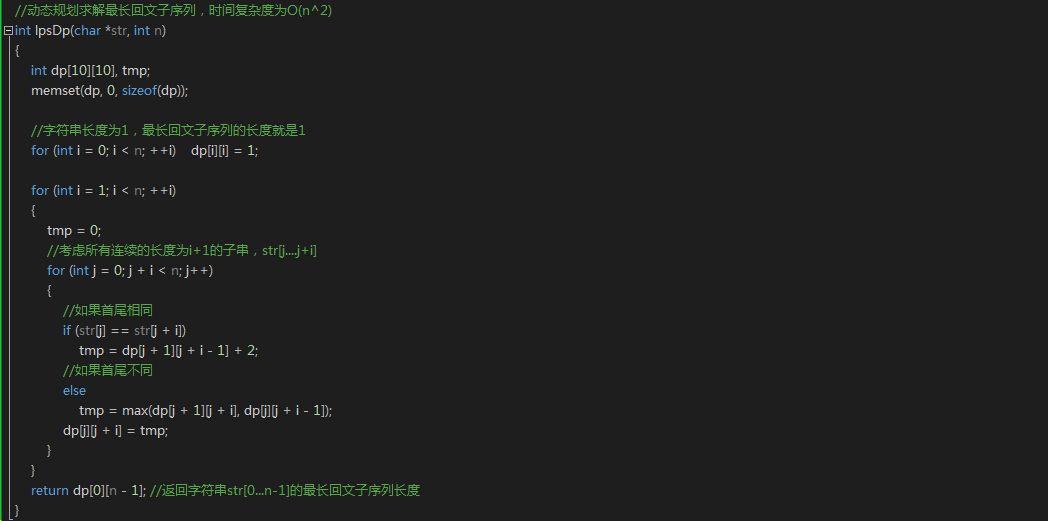
方法二：动态规划方法
通过自下而上的方式记录子问题的最优解
#include<iostream>
#include<algorithm>
using namespace std;
//动态规划求解最长回文子序列，时间复杂度为O(n^2)
int lpsDp(char *str, int n)
{
int dp[10][10], tmp;
memset(dp, 0, sizeof(dp));
for (int i = 0; i < n; ++i) dp[i][i] = 1;
for (int i = 1; i < n; ++i)
{
tmp = 0;
//考虑所有连续的长度为i+1的子串，str[j....j+i]
for (int j = 0; j + i < n; j++)
{
//如果首尾相同
if (str[j] == str[j + i])
tmp = dp[j + 1][j + i - 1] + 2;
//如果首尾不同
else
tmp = max(dp[j + 1][j + i], dp[j][j + i - 1]);
dp[j][j + i] = tmp;
}
}
return dp[0][n - 1]; //返回字符串str[0...n-1]的最长回文子序列长度
}
int main()
{
char str[10] = "cabbeaf";
int res = lpsDp(str, strlen(str));
cout << res << endl;
getchar();
return 0;
}
例1：腾讯2016实习笔试编程题
所谓回文字符串，就是一个字符串，从左到右读和从右到左读是完全一样的，比如“aba”、“c”，对于一个字符串，可以通过删除某些字符而变成回文字符串，如“cabebaf”，删除'c'、'e'、‘f’后剩下子串“abba”就是回文字符串。
要求，给定任意一个字符串，字符串最大长度1000，计算出最长的回文字符串长度。
如“cabebaf”的回文串包括“c”、“aba”、“abba”等，最长回文“abba”长度为4。
Input：字符串
Output：最大的回文字符长度。
Exmaple Inuput：
cabbeaf
Exmaple Output：
4
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1000
//动态规划求解最长回文子序列，时间复杂度为O(n^2)
int lpsDp(char *str, int n)
{
int dp[MAXN>>1][MAXN>>1], tmp;
memset(dp, 0, sizeof(dp));
//字符串长度为1，最长回文子序列的长度就是1
for (int i = 0; i < n; ++i) dp[i][i] = 1;
for (int i = 1; i < n; ++i)
{
tmp = 0;
//考虑所有连续的长度为i+1的子串，str[j....j+i]
for (int j = 0; j + i < n; j++)
{
//如果首尾相同
if (str[j] == str[j + i])
tmp = dp[j + 1][j + i - 1] + 2;
//如果首尾不同
else
tmp = max(dp[j + 1][j + i], dp[j][j + i - 1]);
dp[j][j + i] = tmp;
}
}
return dp[0][n - 1]; //返回字符串str[0...n-1]的最长回文子序列长度
}
int main()
{
char str[MAXN];
while (cin >> str)
{
int res = lpsDp(str, strlen(str));
cout << res << endl;
}
getchar();
return 0;
}
例2：求最长回文子序列长度
题意：
给定字符串，求它的最长回文子序列长度。回文子序列反转字符顺序后仍然与原序列相同。例如字符串abcdfcba中，最长回文子序列长度为7，abcdcba或abcfcba。
思路：
动态规划思想
对于任意字符串，如果头尾字符相同，那么字符串的最长子序列等于去掉首尾的字符串的最长子序列加上首尾；如果首尾字符不同，则最长子序列等于去掉头的字符串的最长子序列和去掉尾的字符串的最长子序列的较大者。
因此动态规划的状态转移方程为：
设字符串为str，长度为n，p[i][j]表示第i到第j个字符间的子序列的个数（i<=j），则：
状态初始条件：dp[i][i]=1 （i=0：n-1）
状态转移方程：dp[i][j]=dp[i+1][j-1] + 2 if（str[i]==str[j]）
dp[i][j]=max(dp[i+1][j],dp[i][j-1]) if （str[i]!=str[j]）
代码：
以下代码中的两层循环变量i,j的顺序可以改变，但必须满足i<=j的条件。
计算dp[i][j]时需要计算dp[i+1][*]或dp[*][j-1]，因此i应该从大到小，即递减；j应该从小到大，即递增。
#include <iostream>
#include <vector>
using namespace std;
int longestPalindromeSubSequence1(string str){
int n=str.length();
vector<vector<int> > dp(n,vector<int>(n));
for(int j=0;j<n;j++){
dp[j][j]=1;
for(int i=j-1;i>=0;i--){
if(str[i]==str[j])
dp[i][j]=dp[i+1][j-1]+2;
else
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][n-1];
}
int longestPalindromeSubSequence2(string str){
int n=str.length();
vector<vector<int> > dp(n,vector<int>(n));
for(int i=n-1;i>=0;i--){
dp[i][i]=1;
for(int j=i+1;j<n;j++){
if(str[i]==str[j])
dp[i][j]=dp[i+1][j-1]+2;
else
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][n-1];
}
int main()
{
string s;
int length;
while(cin>>s){
length=longestPalindromeSubSequence2(s);
cout<<length<<endl;
}
return 0;
}
例3：求回文子序列的个数
给定字符串，求它的回文子序列个数。回文子序列反转字符顺序后仍然与原序列相同。例如字符串aba中，回文子序列为"a", "a", "aa", "b", "aba"，共5个。内容相同位置不同的子序列算不同的子序列。
思路：
动态规划思想
对于任意字符串，如果头尾字符不相等，则字符串的回文子序列个数就等于去掉头的字符串的回文子序列个数+去掉尾的字符串的回文子序列个数-去掉头尾的字符串的回文子序列个数；如果头尾字符相等，那么除了上述的子序列个数之外，还要加上首尾相等时新增的子序列个数，1+去掉头尾的字符串的回文子序列个数，1指的是加上头尾组成的回文子序列，如aa，bb等。
因此动态规划的状态转移方程为：
设字符串为str，长度为n，p[i][j]表示第i到第j个字符间的最长子序列的长度（i<=j），则：
状态初始条件：dp[i][i]=1 （i=0：n-1）
状态转移方程：dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1] if（str[i]！=str[j]）
dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1]+dp[i+1][j-1]+1=dp[i+1][j] + dp[i][j-1]+1 if （str[i]==str[j]）
#include <iostream>
#include <vector>
using namespace std;
int NumOfPalindromeSubSequence(string str){
int len=str.length();
vector<vector<int> > dp(len,vector<int>(len));
for(int j=0;j<len;j++){
dp[j][j]=1;
for(int i=j-1;i>=0;i--){
dp[i][j]=dp[i+1][j]+dp[i][j-1]-dp[i+1][j-1];
if(str[i]==str[j])
dp[i][j]+=1+dp[i+1][j-1];
}
}
return dp[0][len-1];
}
int main()
{
string str;
int num;
while(cin>>str){
num=NumOfPalindromeSubSequence(str);
cout<<num<<endl;
}
return 0;
}
(二）最长回文子串
题目：给定一个字符串s,找出s中的最长回文子串；
暴力法，DP法, 中心扩展法，manacher算法
方法一：暴力法
遍历字符串S的每一个子串，去判断这个子串是不是回文，是回文的话看看长度是不是比最大的长度maxlength大。遍历每一个子串的方法要O（n^2），判断每一个子串是不是回文的时间复杂度是O(n)，所以暴利方法的总时间复杂度是O（n^3）。
public static String findLongestPalindrome(String s){
int len = s.length(); // 字符串长度
int maxlength = 0; // 最长回文字符串长度
int start = 0; // 回文开始的地方
for(int i = 0; i < len; i++){
for(int j = i + 1; j < len; j++){
int index1 = 0;
int index2 = 0;
// 对每个子串都从两边开始向中间遍历
for(index1 = i, index2 = j; index1 < index2; index1 ++, index2--){
if(s.charAt(index1) != s.charAt(index2))
break;
}
// 若index1=index2,表示串是类似于abcba这种类型；若大于，则是abccba这种类型
if(index1 >= index2 && j - i > maxlength){
maxlength = j - i + 1;
start = i;
}
}
}
if(maxlength > 0)
return s.substring(start, start + maxlength);
return null;
}
方法二：动态规划
回文字符串的子串也是回文，比如P[i,j]（表示以i开始以j结束的子串）是回文字符串，那么P[i+1,j-1]也是回文字符串。这样最长回文子串就能分解成一系列子问题了。这样需要额外的空间O（N^2)，算法复杂度也是O(N^2)。
首先定义状态方程和转移方程：
P[i,j]=false:表示子串[i,j]不是回文串。P[i,j]=true:表示子串[i,j]是回文串。
P[i,i]=true:当且仅当P[i+1,j-1] = true && (s[i]==s[j]）
否则p[i,j] =false;
public static String findLongestPalindrome1(String s){
int len = s.length();
int start = 0;
int maxlength = 0;
boolean p[][] = new boolean[s.length()][s.length()];
// 子串长度为1和为2的初始化
for(int i = 0; i < len; i++){
p[i][i] = true;
if(i < len - 1 && s.charAt(i) == s.charAt(i + 1)){
p[i][i + 1] = true;
start = i;
maxlength = 2;
}
}
// 使用上述结果可以dp出子串长度为3~len -1的子串
for(int strlen = 3; strlen < len; strlen ++){
for(int i = 0; i <=len - strlen; i++){
int j = i + strlen - 1; // 子串结束的位置
if(p[i + 1][j - 1] && s.charAt(i) == s.charAt(j)){
p[i][j] = true;
maxlength = strlen;
start = i;
}
}
}
if(maxlength > 0)
return s.substring(start, start + maxlength);
return null;
}
方法三：中心扩展法
中心扩展就是把给定的字符串的每一个字母当做中心，向两边扩展，这样来找最长的子回文串。算法复杂度为O(N^2)。
但是要考虑两种情况：
1、像aba，这样长度为奇数。
2、想abba，这样长度为偶数。
public static String findLongestPalindrome2(String s){
int len = s.length();
int maxlength = 0;
int start = 0;
// 类似于aba这种情况，以i为中心向两边扩展
for(int i = 0; i < len; i++){
int j = i - 1;
int k = i + 1;
while(j >= 0 && k < len && s.charAt(j) == s.charAt(k)){
if(k - j + 1 > maxlength){
maxlength = k - j + 1;
start = j;
}
j --;
k ++;
}
}
// 类似于abba这种情况，以i，i+1为中心向两边扩展
for(int i = 0; i < len; i++){
int j = i;
int k = i + 1;
while(j >= 0 && k <len && s.charAt(j) == s.charAt(k)){
if(k - j + 1 > maxlength){
maxlength = k - j + 1;
start = j;
}
j --;
k ++;
}
}
if(maxlength > 0)
return s.substring(start, start + maxlength);
return null;
}
方法四：Manacher算法
Manacher法只能解决例如aba这样长度为奇数的回文串，对于abba这样的不能解决，于是就在里面添加特殊字符。我是添加了“#”，使abba变为a#b#b#a。这个算法就是利用已有回文串的对称性来计算的，具体算法复杂度为O(N)
详细规则可参考另一篇博客http://blog.sina.com.cn/s/blog_9ca3f6e70102wsb0.html
public static String findLongestPalindrome3(String s) {
if(s == null || s.length() < 1)
return "";
String str = dealWithS(s); // 处理一下s,即将给字符串s的中间加上特殊字符，这样无论对于奇数字符还是偶数字符可以做同样的处理
int[] res = new int[str.length()];
int R = 0; // 当前所能扩展的半径
int C = 0; // C位置的半径为R
int maxC= 0; // 最长的半径的位置
res[0] = 0;
for(int i = 1; i < str.length(); i++)
{
int j = 2 * C - i; // i点的对称点
if(j >= 0 && res[j] < R - i) // 对称点存在且对称点的回文半径在C的回文中
{
res[i] = res[j];
}
else // 否则，需要根据i点一点一点的计算
{
int k = 1;
while(R + k < str.length() && 2 * i - R - k >= 0)
{
if(str.charAt(R + k) == str.charAt(2 * i - R - k))
k ++;
else
break;
}
res[i] = R -i + k - 1;
if(res[i] + i > R)
{
R = res[i] + i;
C = i;
}
}
maxC = res[maxC] > res[i] ? maxC : i; // maxC保存的是回文半径最大的那个点的位置
}
String subStr = str.substring(maxC - res[maxC], maxC + res[maxC] + 1);
StringBuffer sb = new StringBuffer();
for(int i = 0; i < subStr.length(); i++)
{
if(subStr.charAt(i) != '#')
sb.append(subStr.charAt(i));
}
return sb.toString();
}
public static String dealWithS(String s) // 将原字符串进行处理
{
StringBuffer sb = new StringBuffer();
sb.append("#");
for(int i = 0; i < s.length (); i++)
{
sb.append(s.charAt(i));
sb.append("#");
}
return sb.toString();
}
三.相关知识：( 建议放在一起比较区分 )
1）最长上升子序列 ( LIS ) 戳这里～
2）最长公共子序列（LCS）戳这里 ～
宇宙第一小仙女\(^o^)/～～萌量爆表求带飞=≡Σ((( つ^o^)つ~dalao们求关注哦～～
参考资料：
https://www.cnblogs.com/leavescy/p/5878336.html
https://www.cnblogs.com/AndyJee/p/4465696.html
https://blog.youkuaiyun.com/geekmanong/article/details/51056375
扫一扫
677
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
