支持向量机SVM

本文从互联网搬运，只用于本人学习记录。

1. 支持向量

1.1. 线性可分

在二维空间上，两类点被一条直线完全分开叫做线性可分。

1.2. 最大间隔超平面

1.3. 支持向量

样本中距离超平面最近的一些点，这些点叫做支持向量。

1.4. SVM 最优化问题

2. 对偶问题

2.1. 拉格朗日乘数法

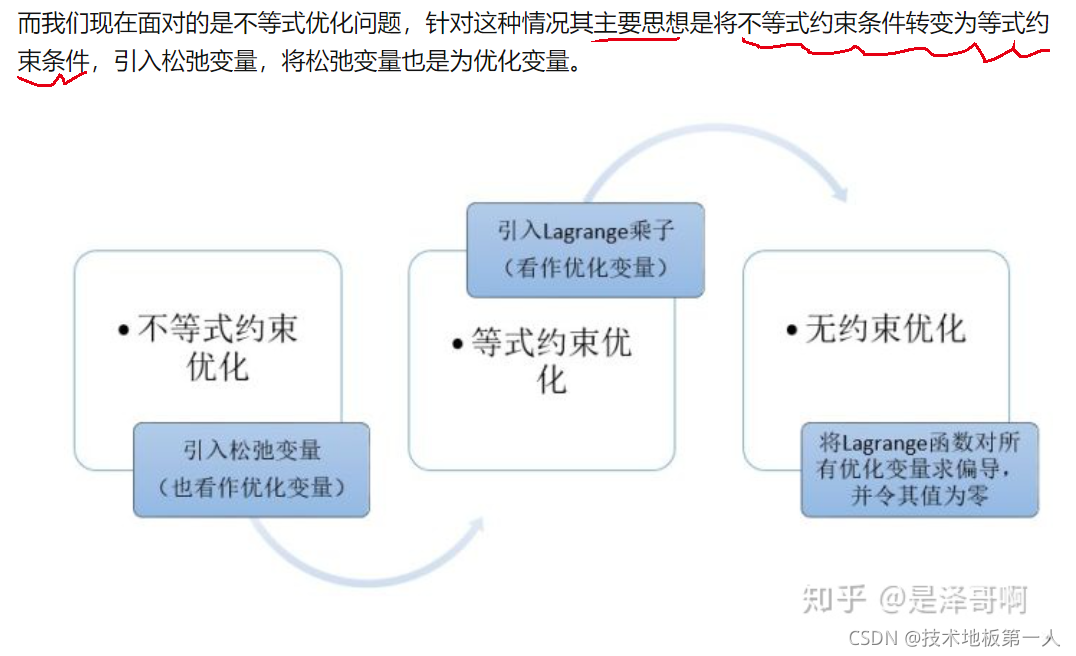
1. 等式约束优化

2. 不等式约束优化

2.2. 强对偶性

3. SVM优化

那么求解线性可分的 SVM 的步骤为：

4. 软间隔

为了解决不能够完全线性可分的样本。

软间隔允许个别样本点出现在间隔带里面。

4.1. 优化目标

5. 核函数

软间隔解决大部分样本点线性可分，小部分样本点线性不可分的情况。

还有一种情况是样本点完全线性不可分
解决办法是将二维线性不可分样本映射到高维空间中，让样本点在高维空间中线性可分。

对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

5.1. 核函数的作用

只是做个内积运算，为什么要有核函数的呢？

这是因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。

核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

5.2. 常见核函数

6. 优缺点

优点：

• 有严格的数学理论支持，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题；
• 能找出对任务至关重要的关键样本（即：支持向量）；
• 采用核技巧之后，可以处理非线性分类/回归任务；
• 最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”。

缺点：

• 训练时间长。当采用 SMO 算法时，由于每次都需要挑选一对参数，因此时间复杂度为$O(N^2)$ ，其中 N 为训练样本的数量；
• 当采用核技巧时，如果需要存储核矩阵，则空间复杂度为$O(N^2)$；
• 模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。

因此支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。