- 一开始先把式子写出来
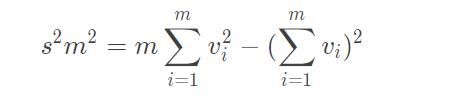
后面的值是固定值所以我们只要最小化前面的式子就可以了 用dp[i][j]来表示前j段路程分成i天走要用的最小天数,很容易可以看出来状态转移方程
这题要求的复杂度显然没那么简单,然后想到用斜率优化来做,我们就可以把状太转移方程调整一下形式
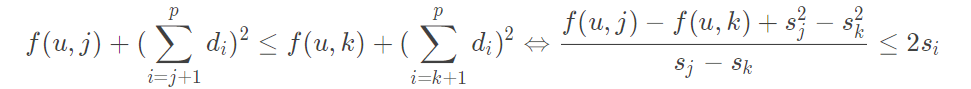
for(int p=2;p<=m;p++){
h=1,t=0;
for(int i=1;i<=n;i++) {
while(h<t&&slp(p-1,que[h],que[h+1])<2*s[i]) h++;//维护队首
int j=que[h];//取最优元素
f[p][i]=f[p-1][j]+(s[j]-s[i])*(s[j]-s[i]); //根据方程写出最优f[p][i]
while(h<t&&slp(p-1,que[t-1],que[t])>slp(p-1,que[t],i))t--;//维护队尾
que[++t]=i;//入队
}
}
这题关键是注意 数学公式的操作,需要看出来他该有的形式




















 329
329

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








