目录
前言
本文发表于期刊IEEE Signal Processing Letters ,发表时间为 2023年 11 月。第一作者张东卫:中共党员,博士,河南科技学院信息工程学院校聘教授。长期从事低可视性图像增强、智慧农业、深度学习等方面的研究。
文献地址:https://ieeexplore.ieee.org/document/10065491
代码地址:https://github.com/Li-Chongyi/PCDE
Abstract-摘要
由于光的吸收和散射,水下采集的图像常常面临严重的质量退化问题。在本文中,我们提出通过分段颜色校正和双重先验优化对比度增强来解决上述问题。首先提出了一种基于最大均值和两个增益因子的逐段颜色校正方法来校正每个颜色通道的偏色。在此基础上,提出了一种基于空间和纹理先验信息的双先验优化对比度增强方法,该方法在HSV颜色空间中对V通道的基本层和细节层进行分解。同时,在不同的层次上采用不同的增强策略来增强水下图像的对比度和纹理细节。在多个基准数据集上的大量对比实验表明,该方法优于11种最先进的方法。此外,该方法对雾天和弱光图像具有较好的泛化能力。
一、Introduction-引言
文章围绕水下图像增强展开,先阐述水下图像因多种因素导致质量下降及现有水下图像增强方法存在的不足,接着介绍了一种名为 PCDE的分段颜色校正和双重先验优化对比度增强的水下图像增强方法及其具体操作,最后强调了该工作在颜色校正以及对比度增强方面的两点贡献。
二、Background-背景
2.1水下成像的重要性与水下图像面临的问题
水下成像在海洋科学考察、水下机器人以及水下物体识别等诸多领域起着重要作用,水下图像是感知和理解水下环境的关键信息载体。然而,由于光的波长依赖型吸收和散射、光照不足以及低端水下成像设备等因素影响,水下图像的颜色和对比度出现了严重的退化情况。例如,光的选择性吸收易造成水下图像出现颜色偏差,光散射则容易致使图像细节模糊、对比度变低。
2.2现有水下图像增强(UIE)方法及局限
目前,解决水下图像质量退化问题的技术主要包括非模型驱动、模型驱动和数据驱动这几类方法。
- 非模型驱动方法:依靠调整图像像素值来提升图像质量,其代表性方法包含基于 Retinex、基于直方图以及基于融合的方法等。例如,Zhang 等人采用最小颜色损失策略校正色偏,并运用自适应对比度增强策略局部提升图像对比度。但这类方法会忽略图像的纹理细节,增强后的图像常出现过饱和现象。
- 模型驱动方法:利用先验信息求解成像模型参数以恢复高可见度图像,其代表性先验包括最小信息损失先验、场景深度先验、统计先验、稀疏先验等。比如,Peng 等人提出了适用于多种图像退化类型的广义暗通道模型,Ding 等人采用全变差正则化进一步细化透射图。不过,这些方法没有充分考虑图像的空间和纹理先验,导致恢复图像的细节锐化不足。
- 数据驱动方法:借助大规模训练数据,利用生成对抗网络(GAN)或图神经网络(GNN)模型的数据驱动方法已成功应用于水下图像增强领域。例如,Song 等人提出了考虑相同水下场景具有相似退化特征的水下图像协同增强网络。同时,强化学习和孪生对抗对比学习也被应用于水下图像增强。然而,高质量训练数据限制了深度学习方法的有效性和鲁棒性。
三、Method-方法

整个流程包含分段颜色校正(PCC)和双重优先优化对比度增强(DPOCE)两部分。
1、在分段颜色校正环节:首先采用最大均值法将每个颜色通道分为两部分。然后,采用两个增益因子的分段颜色校正策略自适应地校正每个颜色通道的偏色。
2、在双重优先优化对比度增强环节:设计了一种双先验优化的对比度增强策略来提高色彩校正图像的质量,其中空间先验被设计为优化和增强图像的基层,纹理先验用于优化和锐化图像的细节层。
3.1分段颜色校正(LACC)
由于水下环境的复杂性和有限的光照条件,水下图像极易受到各种偏色的影响。为了获得高可见度的水下图像,首先要对彩色图像进行校正。
3.1.1分段颜色校正-方法
本文提出了一种分段线性传输的颜色校正方法。首先计算每个颜色通道的灰度平均值,其在数学上表示为:
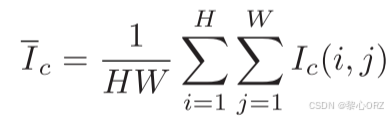
H,W分别是输入图片的高和宽,随后,本文使用以下公式来求解最大灰度均值。
![]()
随后,本文使用参考值对每个颜色通道实施分段校正,其定义为:
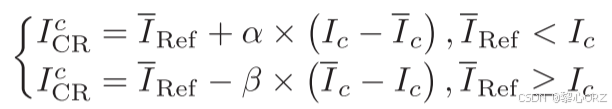
![]()
![]()
表示每个通道的每个部分的增益校正因子。当IRef <Ic时,每个颜色通道的灰度值被拉伸到间隔(IRef,255]。同样,当IRef ≥ Ic时,每个颜色通道的灰度值被拉伸到区间[0,IRef]。最终,校正过程被重新定义为:
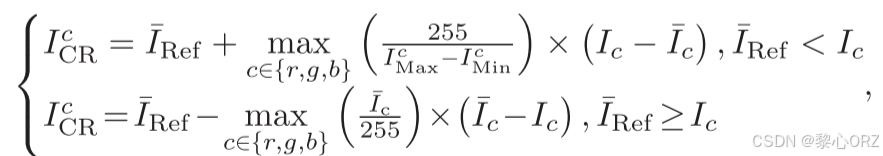
function Final = PCC(I)
R = I(:, :, 1);
G = I(:, :, 2);
B = I(:, :, 3);
avR = mean2(R);
avG = mean2(G);
avB = mean2(B);
Ref = [avR, avG, avB];
Ref = max(Ref);
S1 = max(max(R(:))) - min(min(R(:)));
S2 = max(max(G(:))) - min(min(G(:)));
S3 = max(max(B(:))) - min(min(B(:)));
a = max([double(avR / 255), double(avG / 255), double(avB / 255)]);
b = [double(255 / S1), double(255 / S2), double(255 / S3)];
[m, n] = size(R);
for x = 1:m
for y = 1:n
if R(x, y) <= avR
RC(x, y) = Ref - a * (avR - R(x, y));
else
RC(x, y) = Ref + b(1) * (R(x, y) - avR);
end
if G(x, y) <= avG
GC(x, y) = Ref - a * (avG - G(x, y));
else
GC(x, y) = Ref + b(2) * (G(x, y) - avG);
end
if B(x, y) <= avB
BC(x, y) = Ref - a * (avB - B(x, y));
else
BC(x, y) = Ref + b(3) * (B(x, y) - avB);
end
end
end
Final = cat(3, uint8(RC), uint8(GC), uint8(BC));3.1.2分段颜色校正-结果(验证)
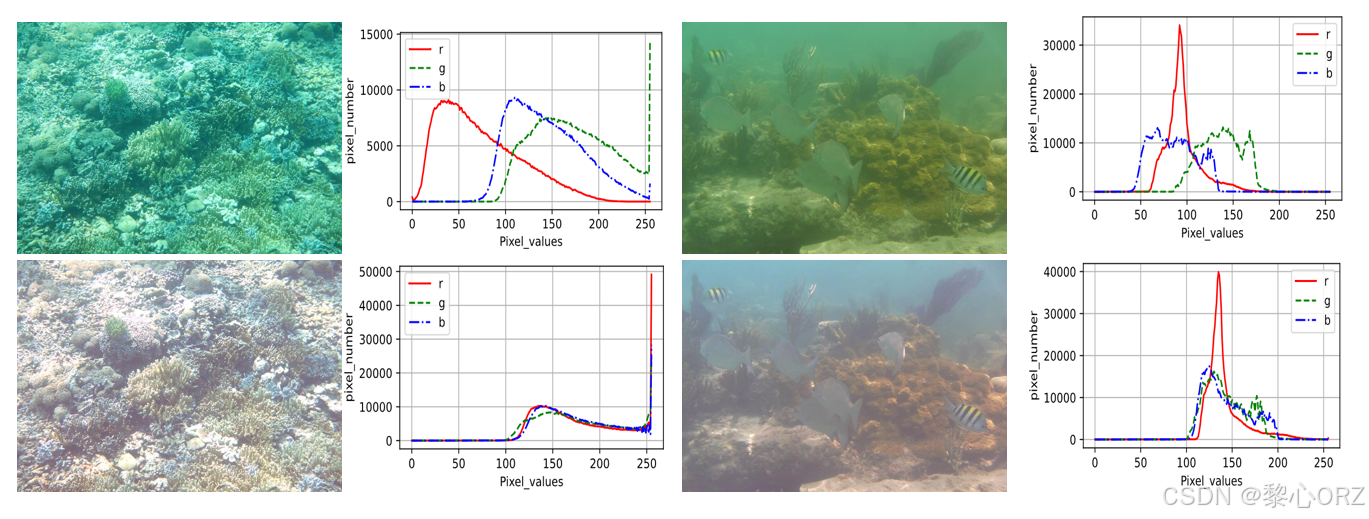
原始图像和经过PCC颜色校正后的图像的三色直方图。上方是原始图像;下方是本文的PCC产生的颜色校正图像。
from PIL import Image
import matplotlib.pyplot as plt
from matplotlib_inline import backend_inline
import numpy as np
class plot:
def __init__(self) -> None:
pass
def use_svg_display(self):
backend_inline.set_matplotlib_formats('svg')
def set_figsize(self,figsize=(3.5,2.5)):
self.use_svg_display()
plt.rcParams['figure.figsize']=figsize
def set_axes(self,axes,xlabel,ylabel,xlim,ylim,xscale,yscale,legend):
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
if legend:
axes.legend(legend)
axes.grid()
def plot(self,X,Y=None,xlabel=None,ylabel=None,legend=None,xlim=None,ylim=None,
xscale='linear',yscale='linear',lengend=None,axes=None,figsize=(3.5,2.5),
fmts=['r','g--','b-.','p:']):
if legend is None:
legend=[]
self.set_figsize(figsize)
axes=axes if axes else plt.gca()
def has_one_axis(X):
return(hasattr(X,"ndim") and X.ndim==1 or isinstance(X,list) and
not hasattr(X[0],"__len__"))
if has_one_axis(X):
X=[X]
if Y is None:
X,Y=[[]]*len(X),X
elif has_one_axis(Y):
Y=[Y]
if len(X) !=len(Y):
X=X*len(Y)
axes.cla()
for x,y,fmt in zip(X,Y,fmts):
axes.plot(x,y,fmt)
self.set_axes(axes,xlabel,ylabel,xlim,ylim,xscale,yscale,legend)
# 读取图像
image = Image.open('../test/1.jpg')
# 获取像素数据
pixels = image.load()
width, height = image.size
# 分别用于存储每个像素位置各通道的值
pixel_values_red = np.zeros(256)
pixel_values_green = np.zeros(256)
pixel_values_blue = np.zeros(256)
for y in range(height):
for x in range(width):
r, g, b = pixels[x, y]
pixel_values_red[r]+=1
pixel_values_green[g]+=1
pixel_values_blue[b]+=1
x=np.arange(0,256,1)
myplot=plot()
myplot.plot(x,[pixel_values_red,pixel_values_green,pixel_values_blue],xlabel='Pixel_values',
ylabel='pixel_number',figsize=(4.5,2.5),legend=['r','g','b'])3.2双重优先优化对比度增强(DPOCE)
3.2.1图片分解
利用空间和纹理先验分解V通道的基本层和细节层,以解决低对比度和细节模糊问题。我们将输入图像、基本层和细节层分别定义为IV、IB和IV-IB。所提出的层分解优化模型以矩阵向量的形式定义为:
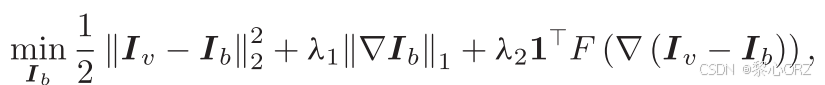
其中和
分别表示
和
的级联向量形式,N表示输入图像的像素的总数,并且
表示不同方向上的梯度运算矩阵的表达式。
强制基层尽可能靠近输入图像。然后,我们在第二项中引入基本层
的空间先验.同时,在第三项
中,细节层的纹理先验,它执行逐个元素的非零运算以产生二进制向量。为了简单起见,我们引入了两个辅助变量
和
替代
和
最后,增广拉格朗日模型被重新定义为:
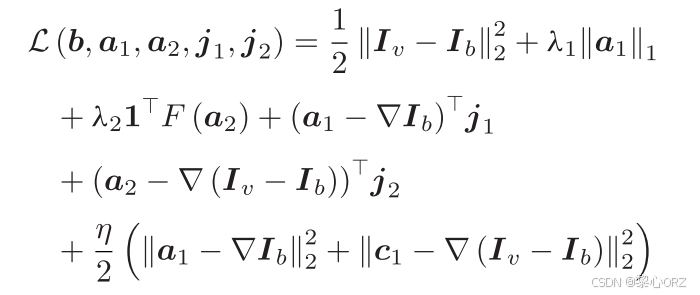
其中j1和j2表示拉格朗日函数的两个变量,η是目标函数迭代更新的参数。本文利用交替方向乘法(ADMM)通过最小化几个子问题和最大化成对问题来迭代优化目标函数。当λ1 =0.25和λ2 =0.025时,广泛的统计分析表明,ADMM可以在20次迭代中有效地分解逼近输入图像的基本层IB。在求解基本层之后,可以通过ID = IV-IB来求解细节层。随后,我们实现不同的增强操作的基础和细节层。

function [D, B] = LLD(S, lambda1, lambda2)
iter = 3;
[hei, wid] = size(S);
fx = [1, - 1];
fy = [1; - 1];
otfFx = psf2otf(fx, [hei, wid]);
otfFy = psf2otf(fy, [hei, wid]);
DxDy = abs(otfFy) .^ 2 + abs(otfFx) .^ 2;
B = S;
C = zeros(hei, wid * 2);
E = zeros(hei, wid * 2);
L1 = zeros(hei, wid * 2);
L2 = zeros(hei, wid * 2);
ro1 = 1;
ro2 = 1;
DiffS = [- imfilter(S, fx, 'circular'), - imfilter(S, fy, 'circular')];
for i = 1:iter
CL = C + L1 ./ ro1;
EL = DiffS - E - L2 ./ ro2;
C1L1 = CL(:, 1:wid);
C2L2 = CL(:, 1 + wid:end);
E1L3 = EL(:, 1:wid);
E2L4 = EL(:, 1 + wid:end);
Nomi = fft2(S) + ro1 .* conj(otfFx) .* fft2(C1L1) + ro1 .* conj(otfFy) .* fft2(C2L2);
+ ro2 .* conj(otfFx) .* fft2(E1L3) + ro2 .* conj(otfFy) .* fft2(E2L4);
Denomi = 1 + (ro1 + ro2) .* DxDy;
B_new = real(ifft2(Nomi ./ Denomi));
DiffB = [- imfilter(B_new, fx, 'circular'), - imfilter(B_new, fy, 'circular')];
BL = DiffB - L1 ./ ro1;
C_new = sign(BL) .* max(abs(BL) - lambda1 ./ ro1, 0);
BL = DiffS - DiffB - L2 ./ ro2;
E_new = BL;
temp = BL .^ 2;
t = temp < 2 .* lambda2 ./ ro2;
E_new(t) = 0;
L1_new = L1 + ro1 * (C_new - DiffB);
L2_new = L2 + ro2 * (E_new - DiffS + DiffB);
ro1 = ro1 * 4;
ro2 = ro2 * 4;
B = B_new;
C = C_new;
E = E_new;
L1 = L1_new;
L2 = L2_new;
end
D = S - B;
end3.2.2基本层增强
在基本层中,充分考虑局部图像块的优势特性,对基本层进行增强。在我们的工作中,局部块K的平均值被近似为低频分量,并且从输入图像块中减去它之后的信息被近似为高频分量。增强细节层的关键是我们如何有效地改善高频成分。为了简单起见,我们以局部图像块K为例。然后,使用积分映射来求解块中的局部均值,并将其用于改进基础层,增强过程定义为:
![]()
其中,是局部图像块的平均值,δ是高频分量的增强控制参数,
是增强的基础层。对统计结果的分析表明,该图像块的大小K和参数δ确定为20 × 20和2时,具有较好的增强能力。为了有效避免局部块增强过程中的伪影或局部黑暗,我们认为Gamma校正策略对于低像素值具有更好的拉伸特性,将公式重新定义为
,其中θ是校正因子参数。根据统计结果分析,θ被设置为0.65。我们使用局部块遍历基本层,直到得到最终的增强基本层
。

I = double(B1);
r=10;
[hei, wid] = size(I);
N = boxfilter(ones(hei, wid), r);
Mean = boxfilter(I, r) ./ N;
p = (Mean + 4.0 * (I - Mean));
v = p;
v = im2double(v);
v = abs((v .^ 0.95));
imwrite(double(v), fullfile(results_dir, [img_name, '_BE.jpg']));3.2.3细节层增强
在细节层,我们考虑锐化图像的纹理结构。随后,我们使用非线性拉伸函数进一步拉伸细节层,该非线性拉伸函数表示如下其中σ是拉伸控制参考,其被设置为0.88。
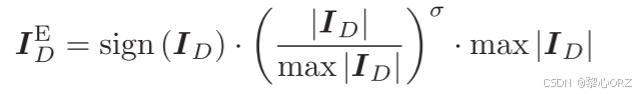

a = 0.88
sigma = max(D1(:));
g = 0
index_low = abs(x - g) <= sigma;
temp = x(index_low);
DE = g + fd(abs(temp - g) ./ sigma, a) .* sigma .* sign(temp - g);
function y = fd(x, a)
y = x .^ a;
end3.3图像融合
随后,我们使用增强的细节层和增强的基础层来获得增强的V通道,其被定义为如下其中是增强的V通道。最后将增强后的图像从HSV色彩空间转换到RGB色彩空间,得到最终的增强图像。
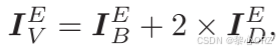


四、summary-总结
本文提出了一种新的水下图像增强方法,首先考虑水下图像的色偏问题。然后,我们使用不同的增强策略来增强的基础层和细节层的V通道在HSV空间分解使用空间先验和纹理先验。定性和定量的比较证明了我们的PCDE对水下图像的良好增强能力。




















 2363
2363

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








