图像分析学习笔记（4）：机器学习图像特征与描述

深度学习基础

• 深度学习概念：深度学习是机器学习的一个分支，它基于一系列算法，试图通过使用多个处理层建立数据的高级抽象模型，这些处理层具有复杂的结构，或者由多个非线性转换组成。–维基百科
• 深度学习发展历史：

模型名称	提出者	年份
Perception	Rosenblatt	1958
RNN	Grossberg	1973
CNN	Fukushima	1979
RBM	Hinton	1999
DBN	Hinton	2006
D-AE	Vincent	2008
AlexNet	Alex	2012
GoogLeNet	Szegedy	2015

• 深度学习的应用：场景识别、视觉类型识别、目标检测、图像题注、语义分割、图像风格迁移、Deep Dream
• 深度学习平台：PyTorch TensorFlow Caffe MatConvNet Theano
• 不同平台的对比：

对比项	Pytorch	Tensorflow
实现方式	命令式编程	符号式编程
图的定义	动态定义	静态定义
运行效率	效率相对低	效率高
学习成本	低	相对高

• 深度学习基本理论
• 学习表示
• 深度学习的步骤：网络构建（一组函数）$\to$学习目标（定义每一函数的好坏）$\to$学习过程（选择最好的函数f）
• 网络构建
  • 神经网络：神经元、权重、偏置、激活函数
  • 计算：矩阵形式
• 学习目标：
  • 训练数据
  • 代价函数（最小），常用代价函数有suare loss Hinge loss Logistic loss Cross entropy loss等
  • 总体代价
• 学习过程
  • 梯度下降法，会面临局部极小值点

深度学习技巧

• 学习阶段：网络构建-学习目标-学习过程
• 测试阶段：训练评价、模型推断、推断评价
• 学习过程
  • 学习率调整策略：后向传播 SGD Mini-Batch SGD 新的激活函数 自适应学习率 Momentum，半监督学习方法 非监督学习方法
  • 前向传播：$$\begin{gathered} z^l=W^{l}x+b^l{a}^l=\sigma (z^l) \\ {z}^l=W^l{a}^{l-1}+b^l{a}^l=\sigma (z^l) \end{gathered}$$
  • 后向传播：$$\begin{gathered} {\delta }^L={\sigma }^{\prime }(z^L)\odot \nabla C(y) \\ {\delta }^l={\sigma }^{\prime }(z^l)\odot (W^{l+1}{)}^T{\delta }^{l+1} \end{gathered}$$
  • 随机梯度下降法（SGD）：模型看到一个训练样本就更新
  • 梯度下降法：看到所有样本后才更新
  • Mini-Batch随机梯度下降法：每次迭代利用B个样本
  • 激活函数：ReLU:快速计算、生物启发、部分解决梯度消失问题
• Adagrad
• 如何解决过拟合：标记更多的训练数据、生成更多的训练数据、迁移学习、改进训练方法、提前停止、权重衰退、DropOut、新的网络结构

深度模型构建

• 卷积神经网络（CNN）
  

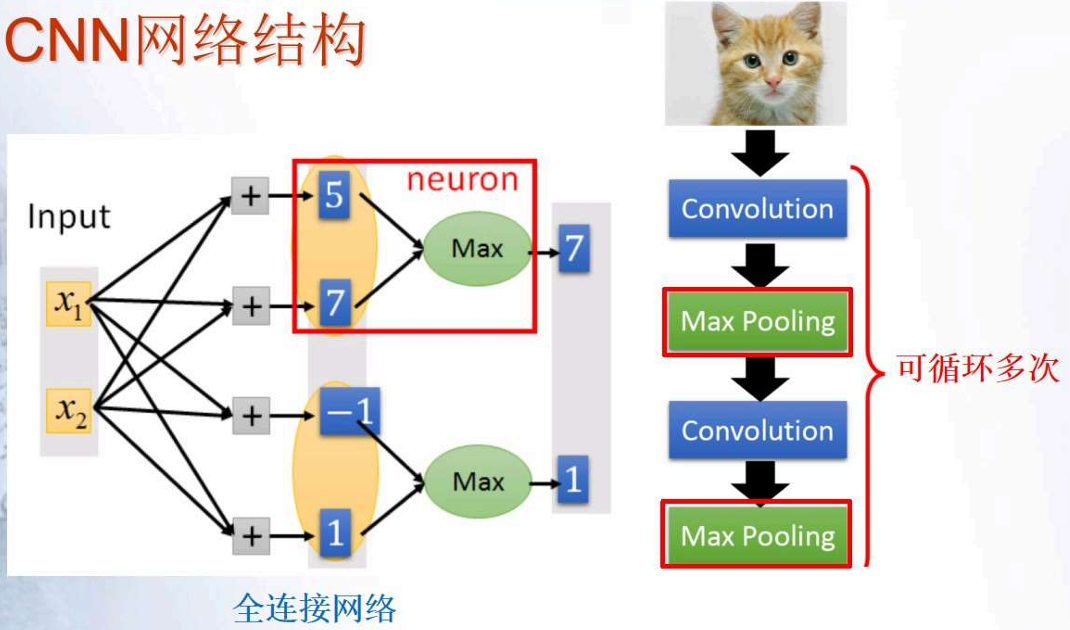
  • 为什么要使用CNN：当处理图像时，全连接网络的第一层可能会非常大，需要根据输入数据和任务简化网络模型
  • 思路发现：邮箱兴趣的模式相对整图很小；同样的模式重复出现在不同的区域；下采样图像通常不会改变目标
  • 性质1：每一个滤波器检测一个局部模式
  • 性质2：局部模式响应

• AlexNet:
  

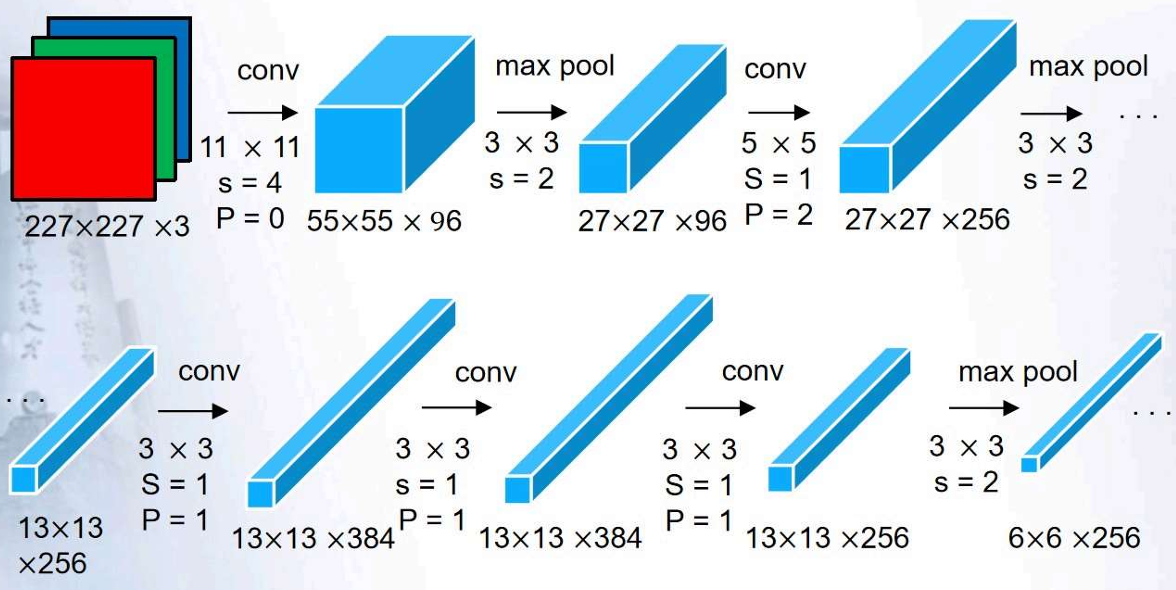
• VGGNet

• GoogleNet

• ResNet:
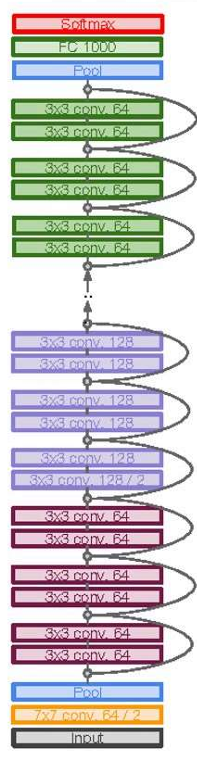
  当堆叠更深层次后的CNN性能反而更差-非常深的模型更加爱难以优化-解决思路：利用网络层次拟合残差映射，替代直接拟合一个潜在目标映射-方法：利用skip connections,可以允许利用一个层次的输出，输入给其他人一层次，利用这些层次你和残差，而不是直接你和H(x)
  残差模块：输入x通过一系列的卷积、relu模块，输出F(X)，将输出结果加到原始的输入x