DS图遍历--深度优先搜索

最新推荐文章于 2024-02-23 13:11:06 发布

原创最新推荐文章于 2024-02-23 13:11:06 发布 · 650 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

DS 专栏收录该内容

47 篇文章

订阅专栏

本文介绍了一种基于深度优先搜索（DFS）的图遍历算法，通过邻接矩阵表示图结构，并从顶点0开始遍历，确保所有顶点均被访问。代码示例展示了如何实现DFS算法，包括处理孤立点的特殊情况。

DS图遍历–深度优先搜索

题目描述

给出一个图的邻接矩阵，对图进行深度优先搜索，从顶点0开始

注意：图n个顶点编号从0到n-1

代码框架如下：
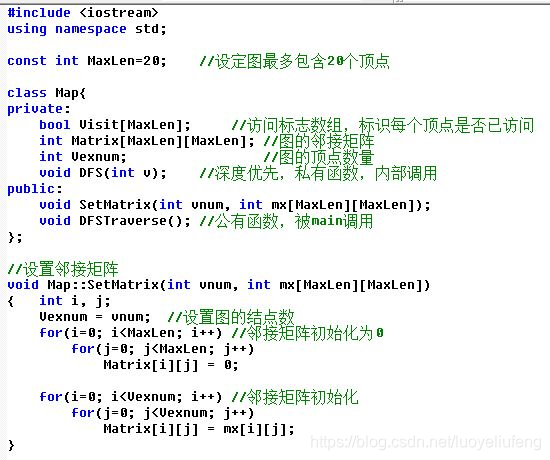
在这里插入图片描述

输入

第一行输入t，表示有t个测试实例

第二行输入n，表示第1个图有n个结点

第三行起，每行输入邻接矩阵的一行，以此类推输入n行

第i个结点与其他结点如果相连则为1，无连接则为0，数据之间用空格隔开

以此类推输入下一个示例

输出

每行输出一个图的深度优先搜索结果，结点编号之间用空格隔开

样例输入

2
4
0 0 1 1
0 0 1 1
1 1 0 1
1 1 1 0
5
0 0 0 1 1
0 0 1 0 0
0 1 0 1 1
1 0 1 0 0
1 0 1 0 0

样例输出

0 2 1 3
0 3 2 1 4

易错点：

孤立点可能未被访问到，见下方代码51行

#include <iostream>
using namespace std;

class Graph{
    int vexNum;
    int **array;
    bool *visit;
    void DFS(int v);
public:
    Graph();
    ~Graph();
    void DFS();
};

Graph::Graph() {
    cin>>vexNum;
    array = new int*[vexNum];
    visit = new bool[vexNum];
    for(int i=0;i<vexNum;i++)
    {
        visit[i]=false;
        array[i] = new int[vexNum];
        for(int j=0;j<vexNum;j++)
            cin>>array[i][j];
    }


}

Graph::~Graph() {
    delete []visit;
    for(int i=0;i<vexNum;i++)
        delete array[i];
    delete array;
}

void Graph::DFS(int v) {
    if(!visit[v])
    {
        visit[v]= true;
        cout<<v<<' ';
        for(int i=0;i<vexNum;i++)
        {
            if(array[v][i]==1)
                DFS(i);
        }
    }
}

void Graph::DFS() {
    for(int i=0;i<vexNum;i++)     //这里是易错点,切忌直接DFS(0);
        DFS(i);
    cout<<endl;
}

int main()
{
    int t;
    cin>>t;
    while (t--)
    {
        Graph myGraph;
        myGraph.DFS();
    }
    return 0;
}