一、快速排序的原理
1、在数组中选中一个数(哨兵),然后寻找该数(哨兵)在本数组中的合适位置,保证把该数(哨兵)放在寻找的位置后,数组左边的全部数比该哨兵的值小,数组右边的全部数值比该哨兵的值小(注意:左右的数并不是顺序排好,只是保证了和哨兵的大小位置)。
2、然后循环第一步的操作,保证全部数值到合适的位置。
二、快排实际演示
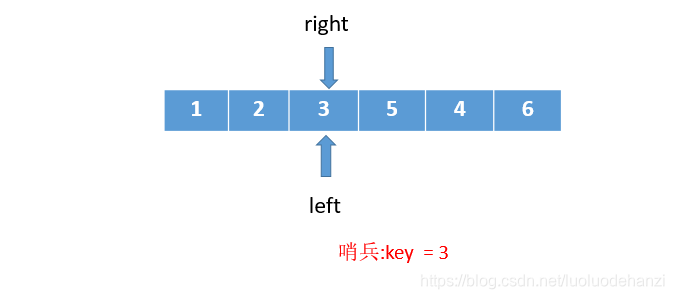
先任意选择一个无序数组。如下:
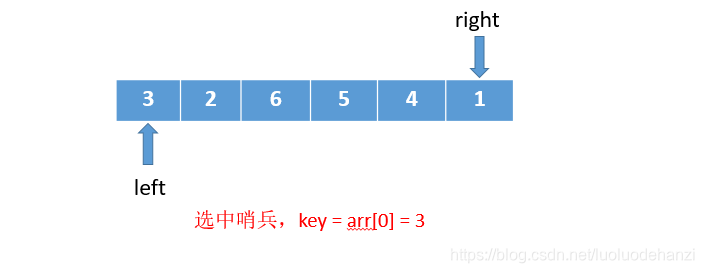
1、设置好数据,从数组右侧开始依次和哨兵大小对比,
如果大于等于哨兵,向左挪动right(right--),
如果小于哨兵,则把该位置的值交换到左侧left所在的位置,
直到right和left重合
移动如下:
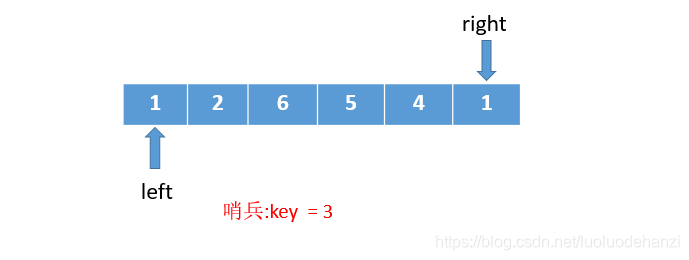
2、第一次对比后交换位置后,然后从数组的左侧开始依次和哨兵大小对比,
如果小于等于哨兵,向右挪动left(left++)
如果大于哨兵,则把该位置的值设置到右侧right所在的位置,
直到right和left重合
移动如下:
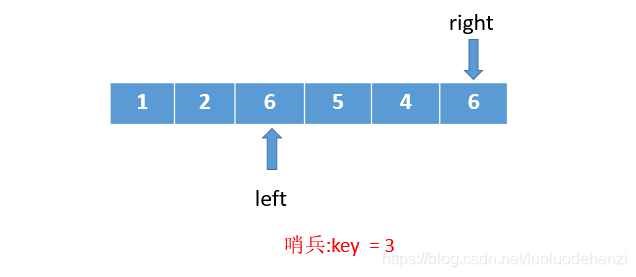
3、第二次对比6和哨兵(key=3)的值,交换6到right所在的位置,
继续第一步操作
移动如下:
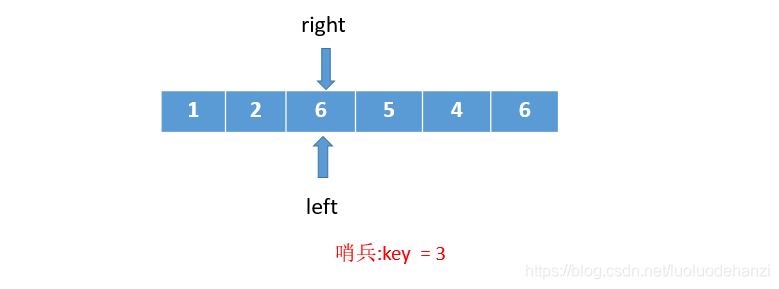
这时候发现left和right重合了,
重合的位置就是哨兵在该数组中的位置(此位置可以确保左边的数都比哨兵小,右边的数都比哨兵大)
设置后的数组如下
4、此时一轮循环已经结束,这时候以哨兵为分割线,分别把左右两半部分按照1-2-3-4步骤循环,最后得到的数组,
每个元素的位置都是最合适的位置,且完成了排序。
三、上代码
1、获取哨兵的合适位置:
//获取哨兵的合适位置
private static int getPickKey(int[] arr,int left,int right){
//获取哨兵
int key = arr[left];
while(left<right){
while(arr[right]>=key && left<right )
right --;
arr[left] = arr[right];
while(arr[left] <=key && left<right )
left ++;
arr[right] = arr[left];
}
arr[right] = key;
return left;
}
2、获取哨兵后,排序左右两部分
//获取哨兵位置后,分割左右,分别对左右两个数组再排序
private static void quickSort(int[]arr,int start,int end){
if(start < end){
int keyIndex = getPickKey(arr,start,end);
quickSort(arr,0,keyIndex-1);
quickSort(arr,keyIndex+1,end);
}
}
3、测试main
public static void main(String[] args) throws InterruptedException {
int [] arr = {65,-2,99,6,8,12,35,24,108,62,31,-1,0,741,54};
quickSort(arr,0,arr.length-1);
for(int i = 0 ;i<arr.length;i++){
System.out.print(arr[i]+",");
}
}
























 1593
1593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








