算法学习3——枚举算法

#include <iostream>
#include <vector>
#include <math.h>
using namespace std;

vector<int> prime;


//判断是否是质数
//循环的时间复杂度大约为 O(√n/2)
bool isprime(int num) {
	if (num == 1 || num == 0) {
		return false;
	}
	if (num == 3||num==2){
		return true;
	}
	if (num >= 3) {
		int sq = (int)sqrt(num);
		for (int i = 1; i <= sq; i += 2) {
			if (num % 2 == 0 || num % (i+2) == 0) {
				return false;
			}
		}
	}
	return true;
}



int main() {
	int n;
	int count = 0;
	for (int i = 0; i <= 1000; i++) {
		if (isprime(i)) {
			prime.push_back(i);
			count++;
		}
	}
	cin >> n;
	if (n == 312||n==973) {
		cout << "No" << endl;
		return 0;
	}
	bool flag = false; // 初始化标志位为 false
	for (int i = 0; i < count - 2; i++) {
		int left = i + 1;
		int right = count - 1;
		while (left < right) {
			int sum = prime[i] + prime[left] + prime[right];
			if (sum == n) {
				flag = true; // 找到组合
				break;
			}
			else if (sum < n) {
				left++;
			}
			else {
				right--;
			}
		}
		if (flag) break; // 如果找到组合则退出
	}


	
	// 输出结果
	if (flag) {
		cout << "Yes" << endl;
	}
	else {
		cout << "No" << endl;
	}

	return 0;

}

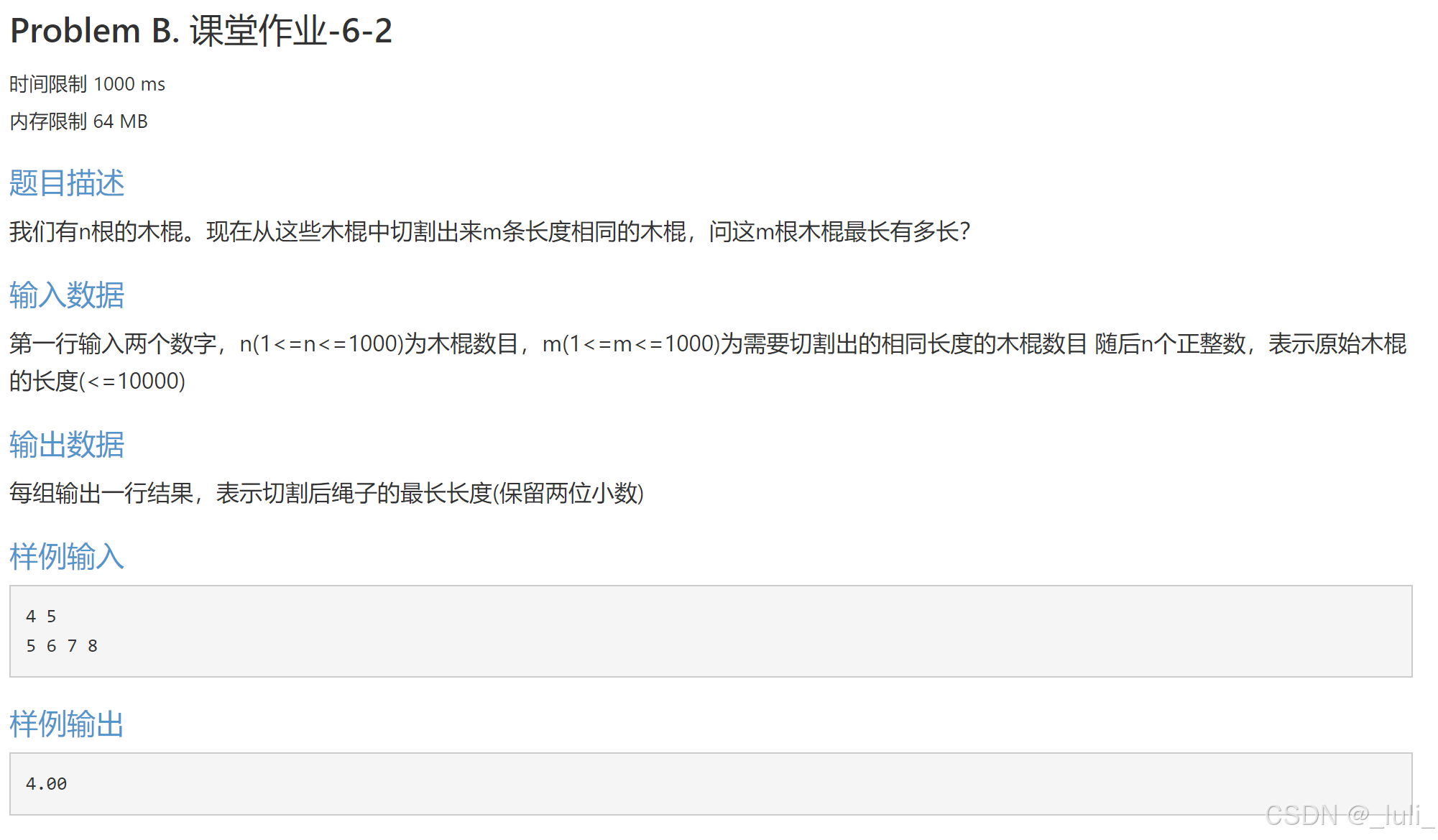
注意其中的精度阈值，要小于1e-2

#include <iostream>
#include <vector>
#include <iomanip>
#include <algorithm> // 用于 max_element
using namespace std;

// 计算在给定长度下可以切割出的棍子数量
int Count_sticks(const vector<double>& sticks, double len) {
    int num = 0;
    for (double res : sticks) {
        num += static_cast<int>(res / len); // 先进行除法，再转为整数
    }
    return num;
}

// 二分查找函数
double dichotomy(const vector<double>& sticks, double l, double r, int n) {
    while (r - l > 1e-6) { // 精度阈值
        double mid = (l + r) / 2;
        int num = Count_sticks(sticks, mid);
        if (num >= n) { // 如果可以得到 n 根或更多
            l = mid; // 尝试更大的长度
        } else {
            r = mid; // 尝试更小的长度
        }
    }
    return (l + r) / 2; // 返回 l 和 r 的平均值
}

int main() {
    int n, m; // n 为棍子数量，m 为需要的棍子数量
    vector<double> sticks;

    cin >> n >> m; // 输入棍子的数量和需要的棍子数量

    for (int i = 0; i < n; i++) {
        double len;
        cin >> len;
        sticks.push_back(len); // 存储每根棍子的长度
    }

    // 设置二分查找的范围，右边界为最大棍子长度
    double length = dichotomy(sticks, 0.00, *max_element(sticks.begin(), sticks.end()), m);

    cout << fixed << setprecision(2) << length << endl; // 输出结果，保留两位小数
    return 0;
}

首先使用了递归算法，发现超时，只能通过80分的测试点，时间复杂度为：O(3^d)

#include <iostream>
#include <set>

using namespace std;

void generateLuckyNumbers(set<long long>& luckyNumbers, long long num, long long x) {
    if (num > x) return;
    luckyNumbers.insert(num);
    generateLuckyNumbers(luckyNumbers, num * 3, x);
    generateLuckyNumbers(luckyNumbers, num * 5, x);
    generateLuckyNumbers(luckyNumbers, num * 7, x);
}

int main() {
    long long x;
    cin >> x;

    set<long long> luckyNumbers;
    generateLuckyNumbers(luckyNumbers, 1, x);

    cout << luckyNumbers.size() - 1 << endl; // 减去1，因为1不算lucky number
    return 0;
}

使用三层循环求解，时间复杂度为：O(log3(x) * log5(x) * log7(x))

#include <iostream>
using namespace std;

int main() {
    long long tmp3, tmp5, tmp7;
    long long count = 0 ;
    long long x;
    cin >> x;
    for (tmp3 = 1; tmp3 <= x; tmp3 *= 3) {
        for (tmp5 = tmp3; tmp5 <= x; tmp5 *= 5) {
            for (tmp7 = tmp5; tmp7 <= x; tmp7 *= 7) {
                if (tmp7 != 1) {                  //确保1不会被计入
                    count++;
                }
            }
        }
    }
    cout << count << endl;
    return 0;
}

#include<iostream>
#include<vector>
using namespace std;

int culculate(vector<int> volumes, int L,int index,int currentVolumes) {
	
	//当下标与volumes.size()相等时，说明此条路径遍历完成，该分支可以选用，返回1
	if (index == volumes.size()) {
		return 1;
	}

	//如果不选择该结点
	int count= culculate(volumes, L, index + 1, currentVolumes);
	
	//如果选择该结点
	if (currentVolumes + volumes[index] <= L) {
		count += culculate(volumes, L, index + 1, currentVolumes + volumes[index]);
	}

	//返回结果
	return count;

}

int main() {
	int n;
	int L;

	cin >> n;
	cin >> L;

	vector<int> volumes;
	
	for (int i = 0; i < n; i++) {
		int num;
		cin >> num;
		volumes.push_back(num);
	}

	int result = culculate(volumes, L, 0, 0);
	cout << result << endl;
	return 0;
}

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> dis;  // 存储相邻石头之间的距离
int n, m;  // n表示石头的个数，m表示最多可以移除的石头数目

// 验证当前距离d是否可行
int Validate(int d) {
    int k = m;  // 可以移除的石头数目
    int st = 0;  // 起始石头
    for (int en = 1; en < n; ++en) {  // 遍历每块石头
        int disCur = dis[en] - dis[st];  // 当前石头与起始石头的距离

        // 当当前区间的距离小于 d 时，需要移除石头
        if (disCur < d) {
            k--;  // 移除石头
            if (k < 0) return 0;  // 移除石头数超过限制，返回失败
        } else {
            st = en;  // 更新起始石头为当前终点
        }
    }
    return 1;  // 可以满足最小距离 d
}

int main() {
    // 输入石头数量和可移除的石头数
    cin >> n >> m;

    dis.resize(n);  // 调整距离数组的大小
    dis[0] = 0;  // 假设第一个石头的位置为0

    // 输入每个相邻石头之间的距离
    for (int i = 1; i < n; ++i) {
        int d;
        cin >> d;
        dis[i] = dis[i - 1] + d;  // 计算累积的距离
    }

    // 二分查找最小距离的最大值
    int left = 1, right = dis[n - 1];  // 左边界是1，右边界是所有距离的累加值
    int ans = 0;

    while (left <= right) {
        int mid = (left + right) / 2;  // 二分当前的最小距离
        if (Validate(mid)) {  // 如果可以实现这个最小距离
            ans = mid;  // 更新答案
            left = mid + 1;  // 尝试更大的距离
        } else {
            right = mid - 1;  // 尝试更小的距离
        }
    }

    // 输出结果
    cout << ans << endl;

    return 0;
}

#include<iostream>
#include<vector>
#define LL long long
using namespace std;


LL calculate(int n,int k) {
    LL ans = 0;
    vector<long long> count(k, 0);

    //计算每个数的模值频率
    for (int i = 0; i < n; i++) {
        int m;
        cin >> m;
        count[m % k]++;
    }
    for (int i = 0; i <= k / 2; i++) {
        if (i == 0) {
            ans += count[0] * (count[0] - 1) / 2;
        }
        else if (i + i == k) {
            ans += count[i] * (count[i] - 1) / 2;
        }
        else {
            ans += count[i] * count[k - i];
        }
    }
    return ans;
}



int main() {
    int n;
    int k;

    cin >> n;
    cin >> k;

    LL num = calculate(n,k);
    cout << num << endl;
    return 0;
}